|
ąŁč鹊čé ą░ą┐ąĮąŠčāčé (ą┐ąĄčĆąĄą▓ąŠą┤ AN4841 [1]) ąŠą┐ąĖčüčŗą▓ą░ąĄčé čĆą░ąĘčĆą░ą▒ąŠčéą║čā čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓ ą┤ą╗čÅ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗčģ čüąĖą│ąĮą░ą╗ąŠą▓ ąĖ čéčĆą░ąĮčüč乊čĆą╝ą░čåąĖą╣ ą╝ąĄąČą┤čā ą┤ąŠą╝ąĄąĮą░ą╝ąĖ ą▓čĆąĄą╝ąĄąĮąĖ ąĖ čćą░čüč鹊čéčŗ. ą×ą▒čüčāąČą┤ą░ąĄą╝čŗąĄ ą▓ čŹč鹊ą╝ ą┤ąŠą║čāą╝ąĄąĮč鹥 ą┐čĆąĖą╝ąĄčĆčŗ ą▓ą║ą╗čÄčćą░čÄčé FIR-čäąĖą╗čīčéčĆčŗ ą▓čŗčüąŠą║ąŠą╣ čćą░čüč鹊čéčŗ ąĖ ąĮąĖąĘą║ąŠą╣ čćą░čüč鹊čéčŗ, ą░ čéą░ą║ąČąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ FFT čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąŠą╣ ąĖ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ ąĮą░ čĆą░ąĘą╗ąĖčćąĮčŗčģ čćą░čüč鹊čéą░čģ.
ą¤čĆąĖą╝ąĄčćą░ąĮąĖąĄ: FIR ąŠąĘąĮą░čćą░ąĄčé Finite-Impulse Response, čé. ąĄ. čäąĖą╗čīčéčĆ čü ą║ąŠąĮąĄčćąĮąŠą╣ ąĖą╝ą┐čāą╗čīčüąĮąŠą╣ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąŠą╣, ąĖą╗ąĖ ąÜąśąź-čäąĖą╗čīčéčĆ. ąŻ čŹč鹊ą│ąŠ čäąĖą╗čīčéčĆą░ ąŠčéčüčāčéčüčéą▓čāčÄčé ąŠą▒čĆą░čéąĮčŗąĄ čüą▓čÅąĘąĖ čü ą▓čŗčģąŠą┤ą░ ąĮą░ ą▓čģąŠą┤ ąĮą░ ą▓ąĄčéą▓čÅčģ čäąĖą╗čīčéčĆą░. FFT ąŠąĘąĮą░čćą░ąĄčé Fast Fourier Transform, čé. ąĄ. ą▒čŗčüčéčĆąŠąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ ążčāčĆčīąĄ.
ąĪąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĄąĄ firmware (X-CUBE-DSPDEMO), ą┐čĆąĄą┤ąĮą░ąĘąĮą░č湥ąĮąĮąŠąĄ ą┤ą╗čÅ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓ (MCU) čüąĄčĆąĖą╣ STM32F429xx ąĖ STM32F746xx, ą╝ąŠąČąĄčé ą▒čŗčéčī ą┐ąŠčĆčéąĖčĆąŠą▓ą░ąĮąŠ ąĮą░ ą╗čÄą▒ąŠą╣ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ STM32.
DSP (Digital Signal Processing, čåąĖčäčĆąŠą▓ą░čÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░ čüąĖą│ąĮą░ą╗ą░, ą”ą×ąĪ) čŹč鹊 ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ą░čÅ ą╝ą░ąĮąĖą┐čāą╗čÅčåąĖčÅ ąĮą░ą┤ ą┤ą░ąĮąĮčŗą╝ąĖ čüąĖą│ąĮą░ą╗ąŠą▓. ąĪąĖą│ąĮą░ą╗čŗ ą┤ą╗čÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ą▓ čĆą░ąĘą╗ąĖčćąĮčŗčģ č乊čĆą╝ą░č鹊ą▓ ą▓ą║ą╗čÄčćą░čé ąĘą▓čāą║, ą▓ąĖą┤ąĄąŠ ąĖą╗ąĖ ą╗čÄą▒ąŠą╣ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗą╣ čüąĖą│ąĮą░ą╗, ą║ąŠč鹊čĆčŗą╣ ąĮąĄčüąĄčé ą▓ čüąĄą▒ąĄ ąĖąĮč乊čĆą╝ą░čåąĖčÄ, čéą░ą║čāčÄ ą║ą░ą║ ą▓čŗčģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗ ą╝ąĖą║čĆąŠč乊ąĮą░.
ą£ąŠą┤ąĄą╗ąĖ MCU, ąŠčüąĮąŠą▓ą░ąĮąĮčŗąĄ ąĮą░ čÅą┤čĆą░čģ Cortex┬«-M4 STM32F4 ąĖ Cortex┬«-M7 STM32F7, ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗čÅčÄčé ąĖąĮčüčéčĆčāą║čåąĖąĖ ą┤ą╗čÅ čüąĖą│ąĮą░ą╗čīąĮąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ, ąĖ ą┐ąŠą┤ą┤ąĄčƹȹĖą▓ą░čÄčé ą┐čĆąŠą┤ą▓ąĖąĮčāčéčŗąĄ ąĖąĮčüčéčĆčāą║čåąĖąĖ SIMD (Single Instruction Multi Data, ąŠą┤ąĮą░ ąĖąĮčüčéčĆčāą║čåąĖčÅ ąĖ ą╝ąĮąŠąČąĄčüčéą▓ąŠ ą┤ą░ąĮąĮčŗčģ) ąŠą┤ąĮąŠčåąĖą║ą╗ąŠą▓čŗąĄ ąĖąĮčüčéčĆčāą║čåąĖąĖ MAC (Multiply and Accumulate, čāą╝ąĮąŠąČąĄąĮąĖąĄ čü ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄą╝).
ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ STM32 MCU ą▓ ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅčģ DSP čĆąĄą░ą╗čīąĮąŠą│ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ąĮąĄ č鹊ą╗čīą║ąŠ čüąĮąĖąČą░ąĄčé čüč鹊ąĖą╝ąŠčüčéčī ąŠą▒ąŠčĆčāą┤ąŠą▓ą░ąĮąĖčÅ, ąĮąŠ čéą░ą║ąČąĄ čüąĮąĖąČą░ąĄčé ąŠą▒čēąĄąĄ 菹ĮąĄčĆą│ąŠą┐ąŠčéčĆąĄą▒ą╗ąĄąĮąĖąĄ čĆąĄą░ą╗ąĖąĘčāąĄą╝ąŠą╣ čüąĖčüč鹥ą╝čŗ.
ŌĆó PM0214 STM32F3 and STM32F4 Series Cortex┬«-M4 programming manual site:st.com.
ŌĆó PM0253 STM32F7 Series Cortex┬«-M7 programming manual site:st.com.
ŌĆó CMSIS - Cortex┬« Microcontroller Software Interface Standard site:arm.com.
ŌĆó Arm┬« compiler toolchain Compiler reference site:infocenter.arm.com.
ŌĆó Developing Optimized Signal Processing Software on the Cortex┬«-M4 Processor site:techonline.com (ą░ą▓č鹊čĆ Shyam Sadasivan).
[DSP: ą▒ą░ąĘąŠą▓čŗąĄ ą┐ąŠąĮčÅčéąĖčÅ]
ąÆ čåąĖčäčĆąŠą▓ąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┐čĆąĖą╝ąĄąĮčÅčÄčéčüčÅ č乊čĆą╝ą░čéčŗ čćąĖčüąĄą╗ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąŠą╣ (floating point) ąĖ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ (fixed point).
Floating point. ąŁč鹊 ą╝ąĄč鹊ą┤ ą┤ą╗čÅ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ čĆąĄą░ą╗čīąĮčŗčģ čćąĖčüąĄą╗. ąæą╗ąŠą║ ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąĖ (Floating Point Unit, FPU [2]) ą▓ Cortex┬«-M4 čĆą░ą▒ąŠčéą░ąĄčé č鹊ą╗čīą║ąŠ čü čćąĖčüą╗ą░ą╝ąĖ ąŠą┤ąĖąĮą░čĆąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ (single precision), ą║ąŠč鹊čĆčŗąĄ ą▓ą║ą╗čÄčćą░čÄčé 8-ą▒ąĖčéąĮąŠąĄ ą┐ąŠą╗ąĄ 菹║čüą┐ąŠąĮąĄąĮčéčŗ (exponent) ąĖ 23-ą▒ąĖčéąĮąŠąĄ ą┐ąŠą╗ąĄ ą┤čĆąŠą▒ąĮąŠą╣ čćą░čüčéąĖ (fraction) ą┤ą╗čÅ 32-ą▒ąĖčéąĮąŠą│ąŠ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ čćąĖčüą╗ą░ (čüą╝. čĆąĖčü. 1).

ąĀąĖčü. 1. ążąŠčĆą╝ą░čé čćąĖčüą╗ą░ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąŠą╣ ąŠą┤ąĖąĮą░čĆąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ (single precision).
ąæą╗ąŠą║ FPU Cortex┬«-M7 ą┐ąŠą┤ą┤ąĄčƹȹĖą▓ą░ąĄčé č乊čĆą╝ą░čé čćąĖčüąĄą╗ ą║ą░ą║ ąŠą┤ąĖąĮąŠčćąĮąŠą╣, čéą░ą║ ąĖ ą┤ą▓ąŠą╣ąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ (double precision), ą║ą░ą║ ą┐ąŠą║ą░ąĘą░ąĮąŠ ąĮą░ čĆąĖčü. 2.

ąĀąĖčü. 2. ążąŠčĆą╝ą░čé čćąĖčüą╗ą░ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąŠą╣ ą┤ą▓ąŠą╣ąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ (double precision).
ąŚąĮą░č湥ąĮąĖąĄ čćąĖčüą╗ą░ ąŠą┤ąĖąĮą░čĆąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ:
Value = (-1)s x M x 2(E-127)
ąŚąĮą░č湥ąĮąĖąĄ čćąĖčüą╗ą░ ą┤ą▓ąŠą╣ąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ:
Value = (-1)s x M x 2(E-1023)
ąŚą┤ąĄčüčī S čŹč鹊 ąĘąĮą░č湥ąĮąĖąĄ ą▒ąĖčéą░ ąĘąĮą░ą║ą░, M ąĘąĮą░č湥ąĮąĖąĄ ą╝ą░ąĮčéąĖčüčüčŗ, E ąĘąĮą░č湥ąĮąĖąĄ 菹║čüą┐ąŠąĮąĄąĮčéčŗ.
Fixed point. ąŁč鹊 ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖąĄ ą▓čŗčĆą░ąČą░ąĄčé čćąĖčüą╗ą░ čü ą┐ąŠą╝ąŠčēčīčÄ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ čåąĄą╗ąŠą╣ čćą░čüčéąĖ (integer part) ąĖ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ ą┤čĆąŠą▒ąĮąŠą╣ čćą░čüčéąĖ (fractional part), ą▓ č乊čĆą╝ą░č鹥 ą┤ą▓ąŠąĖčćąĮąŠą│ąŠ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖčÅ (2-complement format). ąØą░ą┐čĆąĖą╝ąĄčĆ, 32-ą▒ąĖčéąĮą░čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąĖ, ą┐ąŠą║ą░ąĘą░ąĮąĮą░čÅ ąĮą░ čĆąĖčü. 3, ą▓čŗą┤ąĄą╗čÅąĄčé 24 ą▒ąĖčéą░ ą┤ą╗čÅ čåąĄą╗ąŠą╣ čćą░čüčéąĖ 8 ą▒ąĖčéą░ ą┤ą╗čÅ ą┤čĆąŠą▒ąĮąŠą╣ čćą░čüčéąĖ.

ąĀąĖčü. 3. ążąŠčĆą╝ą░čé čćąĖčüą╗ą░ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąĖ.
ąöą╗čÅ čÅą┤ąĄčĆ Cortex┬«-Mx ą┤ąŠčüčéčāą┐ąĮčŗ ą┤ą░ąĮąĮčŗąĄ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ 8, 16 ąĖ 32 ą▒ąĖčéą░.
ąöą╗čÅ ąŠą┐ąĄčĆą░čåąĖą╣ DSP čćą░čēąĄ ą▓čüąĄą│ąŠ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ č乊čĆą╝ą░čéčŗ Q7, Q15 ąĖ Q31, ą│ą┤ąĄ ą▒ąĖčéčŗ ą┤čĆąŠą▒ąĮąŠą╣ čćą░čüčéąĖ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅčÄčé ąĘąĮą░č湥ąĮąĖčÅ č鹊ą╗čīą║ąŠ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ą╝ąĄąČą┤čā -1.0 ąĖ + 1.0.
ą¤čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ čćąĖčüą╗ą░ ą▓ č乊čĆą╝ą░č鹥 Q15:
Value = (-1)bs x (b14 x 2-1 + b13 x 2-2 + ... + b1 x 2-14 + b0 x 2-15)
ąŚą┤ąĄčüčī bs čŹč鹊 ą▒ąĖčé ąĘąĮą░ą║ą░ (15-ą╣ ą▒ąĖčé), ąĖ bn čŹč鹊 ąĘąĮą░č湥ąĮąĖąĄ ą┤ą╗čÅ ą▒ąĖčéą░ n.
ąöąĖą░ą┐ą░ąĘąŠąĮ čćąĖčüąĄą╗, ą┐ąŠą┤ą┤ąĄčƹȹĖą▓ą░ąĄą╝čŗčģ č乊čĆą╝ą░č鹊ą╝ Q15, ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĮčŗčģ ą┤čĆąŠą▒ąĮąŠą╣ čćą░čüčéčīčÄ -1.0 ąĖ 1.0, čüąŠąŠčéą▓ąĄčéčüčéą▓čāąĄčé čüą░ą╝ąŠą╝čā ą╝ą░ą╗ąŠą╝čā ąĖ čüą░ą╝ąŠą╝čā ą▒ąŠą╗čīčłąŠą╝čā čåąĄą╗ąŠą╝čā čćąĖčüą╗čā -32768 ąĖ 32767 čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ.
ąØą░ą┐čĆąĖą╝ąĄčĆ, čćąĖčüą╗ąŠ 0.25 ą▓ č乊čĆą╝ą░č鹥 Q15 ą▒čāą┤ąĄčé ąĘą░ą║ąŠą┤ąĖčĆąŠą▓ą░ąĮąŠ ą║ą░ą║ 0x2000 (8192).
ą¤čĆąĖ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĖ ąŠą┐ąĄčĆą░čåąĖą╣ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ ą▓čŗčĆą░ąČąĄąĮąĖąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčéčüčÅ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝:
c = a < ąŠą┐ąĄčĆą░ąĮą┤ > b
ąŚą┤ąĄčüčī a, b ąĖ c čŹč鹊 čćąĖčüą╗ą░ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ ąĘą░ą┐čÅč鹊ą╣, ąĖ < ąŠą┐ąĄčĆą░ąĮą┤ > ąŠą▒ąŠąĘąĮą░čćą░ąĄčé čüą╗ąŠąČąĄąĮąĖąĄ, ą▓čŗčćąĖčéą░ąĮąĖąĄ, čāą╝ąĮąŠąČąĄąĮąĖąĄ ąĖą╗ąĖ ą┤ąĄą╗ąĄąĮąĖąĄ. ąóąŠ ąČąĄ čüą░ą╝ąŠąĄ ą▓čŗčĆą░ąČąĄąĮąĖąĄ ą┤ąĄą╣čüčéą▓čāąĄčé ąĖ ą┤ą╗čÅ čćąĖčüąĄą╗ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ ąĘą░ą┐čÅč鹊ą╣.
ąŚą░ą╝ąĄčćą░ąĮąĖąĄ: čüą╗ąĄą┤čāąĄčé čāą┤ąĄą╗čÅčéčī ąŠčüąŠą▒ąŠąĄ ą▓ąĮąĖą╝ą░ąĮąĖąĄ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÄ ąŠą┐ąĄčĆą░čåąĖą╣ ąĮą░ą┤ čćąĖčüą╗ą░ą╝ąĖ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ ąĘą░ą┐čÅč鹊ą╣.
ąØą░ą┐čĆąĖą╝ąĄčĆ, ąĄčüą╗ąĖ c = a x b, ą│ą┤ąĄ a ąĖ b ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮčŗ ą▓ č乊čĆą╝ą░č鹥 Q31, č鹊 čŹč鹊 ą┐čĆąĖą▓ąĄą┤ąĄčé ą║ ąĮąĄą┐čĆą░ą▓ąĖą╗čīąĮąŠą╝čā čĆąĄąĘčāą╗čīčéą░čéčā, ą┐ąŠč鹊ą╝čā čćč鹊 ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆ ąŠą▒čĆą░ą▒ąŠčéą░ąĄčé čŹč鹊 ą▓čŗčĆą░ąČąĄąĮąĖąĄ ą║ą░ą║ ąŠą┐ąĄčĆą░čåąĖčÄ ąĮą░ą┤ čåąĄą╗čŗą╝ąĖ čćąĖčüą╗ą░ą╝ąĖ, ą│ąĄąĮąĄčĆąĖčĆčāčÅ ą║ąŠą┤ "muls a, b" ąĖ čüąŠčģčĆą░ąĮąĖčé č鹊ą╗čīą║ąŠ čüą░ą╝čŗąĄ ą╝ą╗ą░ą┤čłąĖąĄ 32 ą▒ąĖčéą░ čĆąĄąĘčāą╗čīčéą░čéą░.
ążąĖą║čüąĖčĆąŠą▓ą░ąĮąĮą░čÅ č鹊čćą║ą░ ą┐čĆąŠčéąĖą▓ ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąĖ. ąóą░ą▒ą╗ąĖčåą░ 1 ą▓čŗčüą▓ąĄčćąĖą▓ą░ąĄčé ąŠčüąĮąŠą▓ąĮčŗąĄ ą┤ąŠčüč鹊ąĖąĮčüčéą▓ą░ ąĖ ąĮąĄą┤ąŠčüčéą░čéą║ąĖ ąŠą┐ąĄčĆą░čåąĖą╣ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąĖ ąĖ ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąĖ ą┤ą╗čÅ ą┐čĆąĖą╗ąŠąČąĄąĮąĖą╣ DSP.
ąóą░ą▒ą╗ąĖčåą░ 1. ąŚą░ ąĖ ą┐čĆąŠčéąĖą▓ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖčÅ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąĖ ąĖ ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąĖ.
| ążąŠčĆą╝ą░čé čćąĖčüą╗ą░ |
Fixed point |
Floating point |
| ąöąŠčüč鹊ąĖąĮčüčéą▓ą░ |
ąæčŗčüčéčĆą░čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ |
ą¤ąŠą┤ą┤ąĄčƹȹ║ą░ čüą░ą╝ąŠą│ąŠ ą▒ąŠą╗čīčłąŠą│ąŠ ą┤ąĖą░ą┐ą░ąĘąŠąĮą░ ąĘąĮą░č湥ąĮąĖą╣ |
| ąØąĄą┤ąŠčüčéą░čéą║ąĖ |
ą×ą│čĆą░ąĮąĖč湥ąĮąĮčŗą╣ ą┤ąĖą░ą┐ą░ąĘąŠąĮ ąĘąĮą░č湥ąĮąĖą╣.
ą×č湥ąĮčī ą┐čĆąŠčüč鹊 ą╝ąŠąČąĄčé ą┐čĆąŠąĖąĘąŠą╣čéąĖ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖąĄ. |
ą¤ąŠą▓čŗčłąĄąĮąĮčŗąĄ čéčĆąĄą▒ąŠą▓ą░ąĮąĖčÅ ą║ ąŠą▒čŖąĄą╝čā ą┐ą░ą╝čÅčéąĖ. |
[ąśąĮčüčéčĆčāą║čåąĖąĖ DSP Cortex┬«]
ą»ą┤čĆą░ Cortex┬«-Mx ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗čÅčÄčé ąĮąĄčüą║ąŠą╗čīą║ąŠ ąĖąĮčüčéčĆčāą║čåąĖą╣, ą┐čĆąĄą┤ąĮą░ąĘąĮą░č湥ąĮąĮčŗčģ ą┤ą╗čÅ čŹčäč乥ą║čéąĖą▓ąĮąŠą╣ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ DSP.
ąśąĮčüčéčĆčāą║čåąĖąĖ ąĮą░čüčŗčēąĄąĮąĖčÅ (saturation). ąśąĮčüčéčĆčāą║čåąĖąĖ ąĮą░čüčŗčēąĄąĮąĖčÅ ą┤ą╗čÅ čüą╗ąŠąČąĄąĮąĖčÅ ąĖ ą▓čŗčćąĖčéą░ąĮąĖčÅ ą┤ąŠčüčéčāą┐ąĮčŗ ą┤ą╗čÅ 8-, 16- ąĖ 32-ą▒ąĖčéąĮčŗčģ ąĘąĮą░č湥ąĮąĖą╣, ąĮąĄą║ąŠč鹊čĆčŗąĄ ąĖąĘ ąĮąĖčģ ą┐ąĄčĆąĄčćąĖčüą╗ąĄąĮčŗ ą▓ čéą░ą▒ą╗ąĖčåąĄ 2.
ąóą░ą▒ą╗ąĖčåą░ 2. ąśąĮčüčéčĆčāą║čåąĖąĖ ąĮą░čüčŗčēąĄąĮąĖčÅ.
| ąÜąŠą┤ |
ążčāąĮą║čåąĖčÅ |
| QADD8 |
ąØą░čüčŗčēąĄąĮąĖąĄ č湥čéčŗčĆąĄčģ 8-ą▒ąĖčéąĮčŗčģ čüą╗ąŠąČąĄąĮąĖą╣ čåąĄą╗čŗčģ čćąĖčüąĄą╗. |
| QSUB8 |
ąØą░čüčŗčēąĄąĮąĖąĄ č湥čéčŗčĆąĄčģ 8-ą▒ąĖčéąĮčŗčģ ą▓čŗčćąĖčéą░ąĮąĖą╣ čåąĄą╗čŗčģ čćąĖčüąĄą╗. |
| QADD16 |
ąØą░čüčŗčēąĄąĮąĖąĄ ą┤ą▓čāčģ 16-ą▒ąĖčéąĮčŗčģ čüą╗ąŠąČąĄąĮąĖą╣ čåąĄą╗čŗčģ čćąĖčüąĄą╗. |
| QSUB16 |
ąØą░čüčŗčēąĄąĮąĖąĄ ą┤ą▓čāčģ 16-ą▒ąĖčéąĮčŗčģ ą▓čŗčćąĖčéą░ąĮąĖą╣ čåąĄą╗čŗčģ čćąĖčüąĄą╗. |
| QADD |
ąØą░čüčŗčēąĄąĮąĖąĄ 32-ą▒ąĖčéąĮąŠą│ąŠ čüą╗ąŠąČąĄąĮąĖčÅ. |
| QSUB |
ąØą░čüčŗčēąĄąĮąĖąĄ 32-ą▒ąĖčéąĮąŠą│ąŠ ą▓čŗčćąĖčéą░ąĮąĖčÅ. |
ąśąĮčüčéčĆčāą║čåąĖčÅ SSAT (ą░ą▒ą▒čĆąĄą▓ąĖą░čéčāčĆą░ ąŠčé Signed SATurate) ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┤ą╗čÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĖ ąĮą░čüčŗčēąĄąĮąĖčÅ ąĘąĮą░č湥ąĮąĖčÅ čüąŠ ąĘąĮą░ą║ąŠą╝ ą┤ą╗čÅ ą╗čÄą▒ąŠą╣ ą┐ąŠąĘąĖčåąĖąĖ ą▒ąĖčéą░, čü ąŠą┐čåąĖąŠąĮą░ą╗čīąĮčŗą╝ čüą┤ą▓ąĖą│ąŠą╝ ą┐ąĄčĆąĄą┤ ąĮą░čüčŗčēąĄąĮąĖąĄą╝.
ąśąĮčüčéčĆčāą║čåąĖčÅ MAC. ąśąĮčüčéčĆčāą║čåąĖąĖ Multiply ACcumulate (MAC, čāą╝ąĮąŠąČąĄąĮąĖąĄ čü ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄą╝) čłąĖčĆąŠą║ąŠ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ ą▓ ą░ą╗ą│ąŠčĆąĖčéą╝ą░čģ DSP, čéą░ą║ąĖčģ ą║ą░ą║ čäąĖą╗čīčéčĆčŗ FIR ąĖ IIR.
ą¤čĆąĖą╝ąĄčćą░ąĮąĖąĄ: ą░ą▒ą▒čĆąĄą▓ąĖą░čéčāčĆą░ IIR ąŠą▒ąŠąĘąĮą░čćą░ąĄčé Infinite Impulse Response, čé. ąĄ. čäąĖą╗čīčéčĆ čü ą▒ąĄčüą║ąŠąĮąĄčćąĮąŠą╣ ąĖą╝ą┐čāą╗čīčüąĮąŠą╣ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąŠą╣ (ąæąśąź), čā ą║ąŠč鹊čĆąŠą│ąŠ ą┐čĆąĖčüčāčéčüčéą▓čāčÄčé ąŠą▒čĆą░čéąĮčŗąĄ čüą▓čÅąĘąĖ čü ą▓čŗčģąŠą┤ą░ ąĮą░ ą▓čģąŠą┤ ąŠčé ą▓ąĄčéą▓ąĄą╣ čäąĖą╗čīčéčĆą░. ąÆčŗą┐ąŠą╗ąĮąĄąĮąĖąĄ MAC ąĘą░ 1 čéą░ą║čé - ą║ą╗čÄč湥ą▓ąŠąĄ čéčĆąĄą▒ąŠą▓ą░ąĮąĖąĄ ą┤ąŠčüčéąĖąČąĄąĮąĖčÅ ą▓čŗčüąŠą║ąŠą╣ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéąĖ DSP.
ąĪą╗ąĄą┤čāčÄčēąĖą╣ ą┐čĆąĖą╝ąĄčĆ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé, ą║ą░ą║ čĆą░ą▒ąŠčéą░ąĄčé ąĖąĮčüčéčĆčāą║čåąĖčÅ SMMLA (Signed Most significant word MuLtiply Accumulate).
SMMLA R0, R4, R5, R6 ; čāą╝ąĮąŠąČą░ąĄčéčüčÅ R4 ąĖ R5, čĆą░čüą┐ą░ą║ąŠą▓čŗą▓ą░čÄčéčüčÅ ą▓ąĄčĆčģąĮąĖąĄ 32 ą▒ąĖčéą░,
; ą┤ąŠą▒ą░ą▓ą╗čÅąĄčéčüčÅ R6, ąŠčéą▒čĆą░čüčŗą▓ą░ąĄčéčüčÅ ąŠčüčéą░č鹊ą║ ąĖ čĆąĄąĘčāą╗čīčéą░čé
; ąĘą░ą┐ąĖčüčŗą▓ą░ąĄčéčüčÅ ą▓ R0.
ąśąĮčüčéčĆčāą║čåąĖąĖ SIMD. ąÆ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖąĄ ą║ ąĖąĮčüčéčĆčāą║čåąĖčÅą╝ MAC, ą║ąŠč鹊čĆčŗąĄ ą┤ąĄą╗ą░čÄčé ąĘą░ 1 čéą░ą║čé čāą╝ąĮąŠąČąĄąĮąĖąĄ čü ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄą╝, čüčāčēąĄčüčéą▓čāčÄčé ąĖąĮčüčéčĆčāą║čåąĖąĖ SIMD (Single Instruction Multiple Data), ą▓čŗą┐ąŠą╗ąĮčÅčÄčēąĖąĄ ąĮąĄčüą║ąŠą╗čīą║ąŠ ąĖą┤ąĄąĮčéąĖčćąĮčŗčģ ąŠą┐ąĄčĆą░čåąĖą╣ ąĘą░ 1 čéą░ą║čé. ąØąĄą║ąŠč鹊čĆčŗąĄ ąĖąĘ čéą░ą║ąĖčģ ąĖąĮčüčéčĆčāą║čåąĖą╣ ą┐ąĄčĆąĄčćąĖčüą╗ąĄąĮčŗ ą▓ čéą░ą▒ą╗ąĖčåąĄ 3.
ąóą░ą▒ą╗ąĖčåą░ 3. ąśąĮčüčéčĆčāą║čåąĖąĖ SIMD.
| ąÜąŠą┤ |
ążčāąĮą║čåąĖčÅ |
| __qadd16 |
ąÆčŗą┐ąŠą╗ąĮčÅąĄčé ą┤ą▓ą░ 16-ą▒ąĖčéąĮčŗčģ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮčŗčģ ą░čĆąĖčäą╝ąĄčéąĖč湥čüą║ąĖčģ čüą╗ąŠąČąĄąĮąĖą╣ ą┐ą░čĆą░ą╗ą╗ąĄą╗čīąĮąŠ, čü ąĮą░čüčŗčēąĄąĮąĖąĄą╝ čĆąĄąĘčāą╗čīčéą░č鹊ą▓ ą┤ąŠ 16-ą▒ąĖčéąĮąŠą│ąŠ čåąĄą╗ąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ čüąŠ ąĘąĮą░ą║ąŠą╝ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ -215 Ōēż x Ōēż 215 - 1. |
| __uhadd16 |
ąÆčŗą┐ąŠą╗ąĮčÅąĄčé ą┤ą▓ą░ čüą╗ąŠąČąĄąĮąĖčÅ 16-ą▒ąĖčéąĮčŗčģ čåąĄą╗čŗčģ čćąĖčüąĄą╗ ą▒ąĄąĘ ąĘąĮą░ą║ą░, čü ą┤ąĄą╗ąĄąĮąĖąĄą╝ ą┐ąŠą┐ąŠą╗ą░ą╝ čĆąĄąĘčāą╗čīčéą░čéą░. |
| __shadd18 |
ąÆčŗą┐ąŠą╗ąĮčÅąĄčé ąŠą┐ąĄčĆą░čåąĖąĖ čüą╗ąŠąČąĄąĮąĖčÅ č湥čéčŗčĆąĄčģ 8-ą▒ąĖčéąĮčŗčģ čåąĄą╗čŗčģ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝, čü ą┤ąĄą╗ąĄąĮąĖąĄą╝ ą┐ąŠą┐ąŠą╗ą░ą╝ čĆąĄąĘčāą╗čīčéą░č鹊ą▓. |
| __smlsd |
ąÆčŗą┐ąŠą╗ąĮčÅąĄčé ą┤ą▓ą░ 16-ą▒ąĖčéąĮčŗčģ čāą╝ąĮąŠąČąĄąĮąĖą╣ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝, ą┐čĆąĖąĮąĖą╝ą░ąĄčé čĆą░ąĘąĮąĖčåčā čĆąĄąĘčāą╗čīčéą░č鹊ą▓, ą▓čŗčćąĖčéą░ąĄčé čüčéą░čĆčłčāčÄ ą┐ąŠą╗ąŠą▓ąĖąĮčā čüą╗ąŠą▓ą░ ąĖąĘ ą╝ą╗ą░ą┤čłąĄą╣ ą┐ąŠą╗ąŠą▓ąĖąĮčŗ čüą╗ąŠą▓ą░ čĆąĄąĘčāą╗čīčéą░čéą░, ąĖ ą┤ąŠą▒ą░ą▓ą╗čÅąĄčé čĆą░ąĘąĮąĖčåčā ą║ 32-ą▒ąĖčéąĮąŠą╝čā ąŠą┐ąĄčĆą░ąĮą┤čā ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖčÅ. |
ąĪą╗ąĄą┤čāčÄčēąĖą╣ ą┐čĆąĖą╝ąĄčĆ ąŠą▒čŖčÅčüąĮčÅąĄčé, ą║ą░ą║ čĆą░ą▒ąŠčéą░ąĄčé ąĖąĮčüčéčĆčāą║čåąĖčÅ __shadd8.
unsigned int add_and_halve (unsigned int val1, unsigned int val2)
{
unsigned int res;
res = __shadd8(val1, val2); // res[7:0] = (val1[7:0] +val2[7:0]) >> 1
// res[15:8] = (val1[15:8] +val2[15:8]) >> 1
// res[23:16] = (val1[23:16]+val2[23:16]) >> 1
// res[31:24] = (val1[31:24]+val2[31:24]) >> 1
return res;
}
ąÆčüčéčĆąŠąĄąĮąĮčŗą╣ ąŠą▒čŖąĄą║čé ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆą░ (intrinsic) __shadd8 ą▓ąŠąĘą▓čĆą░čéąĖčé:
ŌĆó ą¤ąŠą┤ąĄą╗ąĄąĮąĮčŗą╣ ąĮą░ 2 čĆąĄąĘčāą╗čīčéą░čé čüą╗ąŠąČąĄąĮąĖčÅ ą┐ąĄčĆą▓čŗčģ ą▒ą░ą╣čé ą║ą░ąČą┤ąŠą│ąŠ ąŠą┐ąĄčĆą░ąĮą┤ą░, ą▓ ą┐ąĄčĆą▓ąŠą╝ ą▒ą░ą╣č鹥 ą▓ąŠąĘą▓čĆą░čēą░ąĄą╝ąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ.
ŌĆó ą¤ąŠą┤ąĄą╗ąĄąĮąĮčŗą╣ ąĮą░ 2 čĆąĄąĘčāą╗čīčéą░čé čüą╗ąŠąČąĄąĮąĖčÅ ą▓č鹊čĆčŗčģ ą▒ą░ą╣čé ą║ą░ąČą┤ąŠą│ąŠ ąŠą┐ąĄčĆą░ąĮą┤ą░, ą▓ąŠ ą▓č鹊čĆąŠą╝ ą▒ą░ą╣č鹥 ą▓ąŠąĘą▓čĆą░čēą░ąĄą╝ąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ.
ŌĆó ą¤ąŠą┤ąĄą╗ąĄąĮąĮčŗą╣ ąĮą░ 2 čĆąĄąĘčāą╗čīčéą░čé čüą╗ąŠąČąĄąĮąĖčÅ čéčĆąĄčéčīąĖčģ ą▒ą░ą╣čé ą║ą░ąČą┤ąŠą│ąŠ ąŠą┐ąĄčĆą░ąĮą┤ą░, ą▓ čéčĆąĄčéčīąĄą╝ ą▒ą░ą╣č鹥 ą▓ąŠąĘą▓čĆą░čēą░ąĄą╝ąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ.
ŌĆó ą¤ąŠą┤ąĄą╗ąĄąĮąĮčŗą╣ ąĮą░ 2 čĆąĄąĘčāą╗čīčéą░čé čüą╗ąŠąČąĄąĮąĖčÅ č湥čéą▓ąĄčĆčéčŗčģ ą▒ą░ą╣čé ą║ą░ąČą┤ąŠą│ąŠ ąŠą┐ąĄčĆą░ąĮą┤ą░, ą▓ č湥čéą▓ąĄčĆč鹊ą╝ ą▒ą░ą╣č鹥 ą▓ąŠąĘą▓čĆą░čēą░ąĄą╝ąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ.
[ąÉą╗ą│ąŠčĆąĖčéą╝čŗ]
ążąĖą╗čīčéčĆ. ą¦ą░čēąĄ ą▓čüąĄą│ąŠ čäąĖą╗čīčéčĆčŗ ą▒čŗą▓ą░čÄčé:
ŌĆó FIR (Finite Impulse Response): ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ, ą┐ąŠą╝ąĖą╝ąŠ ą▓čüąĄą│ąŠ ą┐čĆąŠč湥ą│ąŠ, ą▓ čāą┐čĆą░ą▓ą╗ąĄąĮąĖąĖ ą┤ą▓ąĖą│ą░č鹥ą╗čÅą╝ąĖ, 菹║ą▓ą░ą╗ą░ą╣ąĘąĄčĆą░čģ ąĘą▓čāą║ą░.
ŌĆó IIR (Infinite Impulse Response): ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┤ą╗čÅ čāą╗čāčćčłąĄąĮąĖčÅ ą┤ą░ąĮąĮčŗčģ. IIR-čäąĖą╗čīčéčĆ ą╝ąŠąČąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ą┤ą╗čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čéą░ą║ąĖčģ čäąĖą╗čīčéčĆąŠą▓, ą║ą░ą║ čäąĖą╗čīčéčĆčŗ ąæą░čéč鹥čĆą▓ąŠčĆčéą░ (Butterworth), ą¦ąĄą▒čŗčłąĄą▓ą░ (Chebyshev) ąĖ ąæąĄčüčüąĄą╗čÅ (Bessel).
ą¤čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ. ąŁč鹊 čäčāąĮą║čåąĖčÅ, ą║ąŠč鹊čĆą░čÅ ą┐čĆąĄąŠą▒čĆą░ąĘčāąĄčé (transform) ą┤ą░ąĮąĮčŗąĄ ąĖąĘ ąŠą┤ąĮąŠą│ąŠ ą┤ąŠą╝ąĄąĮą░ ą▓ ą┤čĆčāą│ąŠą╣. ąóąĖą┐ąĖčćąĮčŗą╣ ą┐čĆąĖą╝ąĄčĆ čŹč鹊 FFT (Fast Fourier Transform): čŹčäč乥ą║čéąĖą▓ąĮčŗą╣ ą░ą╗ą│ąŠčĆąĖčéą╝, ąĖčüą┐ąŠą╗čīąĘčāąĄą╝čŗą╣ ą┤ą╗čÅ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ą┤ąĖčüą║čĆąĄčéąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ ąĖąĘ ą┤ąŠą╝ąĄąĮą░ ą▓čĆąĄą╝ąĄąĮąĖ ą▓ 菹║ą▓ąĖą▓ą░ą╗ąĄąĮčéąĮčŗą╣ čüąĖą│ąĮą░ą╗ ą▓ ą┤ąŠą╝ąĄąĮąĄ čćą░čüč鹊čéčŗ, čĆą░ą▒ąŠčéą░čÄčēąĖą╣ ąĮą░ ąŠčüąĮąŠą▓ąĄ Discrete Fourier Transform (DFT).
[ąĀą░ąĘčĆą░ą▒ąŠčéą║ą░ ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ DSP]
Cortex┬« Microcontroller Software Interface Standard (CMSIS) čŹč鹊 čüą╗ąŠą╣ ą░ą▒čüčéčĆą░ą║čåąĖąĖ ąŠčé ą░ą┐ą┐ą░čĆą░čéčāčĆčŗ, čāčüčéčĆą░ąĮčÅčÄčēąĖą╣ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ąŠčé ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čÅ ą┤ą╗čÅ ą▓čüąĄčģ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓, ąŠčüąĮąŠą▓ą░ąĮąĮčŗčģ ąĮą░ čÅą┤čĆąĄ Cortex┬«.
CMSIS čĆą░ąĘčĆą░ą▒ąŠčéą░ą╗ą░ ąŠčĆą│ą░ąĮąĖąĘą░čåąĖčÅ Arm┬« ą▓ą╝ąĄčüč鹥 čü ą┐ą░čĆčéąĮąĄčĆą░ą╝ąĖ - ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čÅą╝ąĖ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓ (MCU), ą┐čĆąŠą│čĆą░ą╝ą╝ąĮčŗčģ ąĖąĮčüčéčĆčāą╝ąĄąĮč鹊ą▓ (ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆąŠą▓) ąĖ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ ą┐čĆąŠą╝ąĄąČčāč鹊čćąĮčŗčģ ą▒ąĖą▒ą╗ąĖąŠč鹥ą║ (middleware).
ąśą┤ąĄčÅ CMSIS ą▓ č鹊ą╝, čćč鹊ą▒čŗ ą┐čĆąĄą┤ąŠčüčéą░ą▓ąĖčéčī čåąĄą╗ąŠčüčéąĮąŠčüčéąĮčŗą╣ ąĖ ą┐čĆąŠčüč鹊ą╣ ą┐čĆąŠą│čĆą░ą╝ą╝ąĮčŗą╣ ąĖąĮč鹥čĆč乥ą╣čü ą║ ą░ą┐ą┐ą░čĆą░čéčāčĆąĄ MCU, ą┤ą░čÄčēąĖą╣ ą┤ąŠčüčéčāą┐ ą║ ą┐ąĄčĆąĖč乥čĆąĖą╣ąĮčŗą╝ čāčüčéčĆąŠą╣čüčéą▓ą░ą╝, ąŠą┐ąĄčĆą░čåąĖąŠąĮąĮčŗą╝ čüąĖčüč鹥ą╝ą░ą╝ čĆąĄą░ą╗čīąĮąŠą│ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ąĖ ą▒ąĖą▒ą╗ąĖąŠč鹥ą║ą░ą╝ ą┐ąŠą┤ą┤ąĄčƹȹ║ąĖ. CMSIS ą┐čĆąĖąĘą▓ą░ąĮą░ čāą┐čĆąŠčüčéąĖčéčī ą┐ąŠą▓č鹊čĆąĮąŠąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą║ąŠą┤ą░, čüąĮąĖąČąĄąĮąĖąĄ ą▓čĆąĄą╝ąĄąĮąĖ ąŠą▒čāč湥ąĮąĖčÅ ąĖ čĆą░ąĘčĆą░ą▒ąŠčéą║ąĖ, ąĖ ą▓ čāčüą║ąŠčĆąĄąĮąĖčÅ ą▓čŗčģąŠą┤ą░ ąĮą░ čĆčŗąĮąŠą║ ą║ąŠąĮąĄčćąĮčŗčģ ą┐čĆąŠą┤čāą║č鹊ą▓, ąŠčüąĮąŠą▓ą░ąĮąĮčŗčģ ąĮą░ ąĮąŠą▓čŗčģ MCU.
ąæąĖą▒ą╗ąĖąŠč鹥ą║ą░ CMSIS ą┐ąŠčüčéą░ą▓ą╗čÅąĄčéčüčÅ ą▓ą╝ąĄčüč鹥 firmware ąŠčé ST, ą▓ ą║ą░čéą░ą╗ąŠą│ąĄ \Drivers\CMSIS\.
ąæąĖą▒ą╗ąĖąŠč鹥ą║ą░ CMSIS-DSP ą▓ą║ą╗čÄčćą░ąĄčé:
ŌĆó ąæą░ąĘąŠą▓čŗąĄ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąĖą╣ čäčāąĮą║čåąĖąĖ ą┤ą╗čÅ ąŠą┐ąĄčĆą░čåąĖąĖ ąĮą░ą┤ ą▓ąĄą║č鹊čĆą░ą╝ąĖ (ą╝ą░čüčüąĖą▓ą░ą╝ąĖ).
ŌĆó ąæčŗčüčéčĆčŗąĄ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąĖąĄ čäčāąĮą║čåąĖąĖ, ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ čüąĖąĮčāčüą░ ąĖ ą║ąŠčüąĖąĮčāčüą░ (sine, cosine).
ŌĆó ąĪą╗ąŠąČąĮčŗąĄ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąĖąĄ čäčāąĮą║čåąĖąĖ ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą╝ą░ą│ąĮąĖčéčāą┤čŗ.
ŌĆó ążčāąĮą║čåąĖąĖ čäąĖą╗čīčéčĆą░čåąĖąĖ ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ FIR ąĖą╗ąĖ IIR.
ŌĆó ążčāąĮą║čåąĖąĖ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą╝ą░čéčĆąĖčå.
ŌĆó ążčāąĮą║čåąĖąĖ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ FFT.
ŌĆó ążčāąĮą║čåąĖąĖ ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ PID.
ŌĆó ąĪčéą░čéąĖčüčéąĖč湥čüą║ąĖąĄ čäčāąĮą║čåąĖąĖ, ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą╝ąĖąĮąĖą╝čāą╝ą░ ąĖ ą╝ą░ą║čüąĖą╝čāą╝ą░.
ŌĆó ąĪąĄčĆą▓ąĖčüąĮčŗąĄ čäčāąĮą║čåąĖąĖ ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ąĖąĘ ąŠą┤ąĮąŠą│ąŠ č乊čĆą╝ą░čéą░ ą┤ą░ąĮąĮčŗčģ ą▓ ą┤čĆčāą│ąŠą╣.
ŌĆó ążčāąĮą║čåąĖąĖ ąĖąĮč鹥čĆą┐ąŠą╗čÅčåąĖąĖ.
ąæąŠą╗čīčłąĖąĮčüčéą▓ąŠ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ ąĖčüą┐ąŠą╗čīąĘčāąĄčé čćąĖčüą╗ą░ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ ąĘą░ą┐čÅč鹊ą╣ (floating-point) ąĖ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ ąĘą░ą┐čÅč鹊ą╣ (fixed-point) ą▓ čĆą░ąĘą╗ąĖčćąĮčŗčģ č乊čĆą╝ą░čéą░čģ. ąØą░ą┐čĆąĖą╝ąĄčĆ ą┤ą╗čÅ čüą╗čāčćą░čÅ FIR ą┤ąŠčüčéčāą┐ąĮčŗ čäčāąĮą║čåąĖąĖ Arm┬«:
arm_fir_init_f32
arm_fir_f32
arm_fir_init_q31
arm_fir_q31
arm_fir_fast_q31
arm_fir_init_q15
arm_fir_q15
arm_fir_fast_q15
arm_fir_init_q7
arm_fir_q7
ą×ą▒ąĘąŠčĆ ą┤ąĄą╝ąŠąĮčüčéčĆą░čåąĖąŠąĮąĮčŗčģ ą┐čĆąĖą╗ąŠąČąĄąĮąĖą╣ DSP. ą”ąĄą╗čī čŹč鹊ą╣ ą┤ąĄą╝ąŠąĮčüčéčĆą░čåąĖąĖ - ą┐ąŠą║ą░ąĘą░čéčī ą┐ąŠą╗ąĮčāčÄ ąĖąĮč鹥ą│čĆą░čåąĖčÄ čü STM32F429 ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ ADC, DAC, DMA ąĖ čéą░ą╣ą╝ąĄčĆąŠą▓, ą░ čéą░ą║ąČąĄ ą▓čŗąĘąŠą▓čŗ ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝ CMSIS. ąÆčüąĄ čŹč鹊 čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ ą│čĆą░čäąĖą║ąĖ, ąŠč鹊ą▒čĆą░ąČą░ąĄą╝ąŠą╣ ąĮą░ 2.4" QVGA TFT LCD, čāčüčéą░ąĮąŠą▓ą╗ąĄąĮąĮąŠą╝ ąĮą░ ą┐ą╗ą░č鹥 Discovery [3]. ąöąĄą╝ąŠąĮčüčéčĆą░čåąĖčÅ čéą░ą║ąČąĄ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą┐čĆąŠčüč鹊čéčā ą╝ąĖą│čĆą░čåąĖąĖ čü ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ STM32F4 ąĮą░ ąŠą┤ąĖąĮ ąĖąĘ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓ čüąĄčĆąĖąĖ STM32F7.
ąōčĆą░čäąĖč湥čüą║ąĖą╣ ąĖąĮč鹥čĆč乥ą╣čü ą┐ąŠą╗čīąĘąŠą▓ą░č鹥ą╗čÅ čĆą░ąĘčĆą░ą▒ąŠčéą░ąĮ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ STemWin, čćč鹊ą▒čŗ čāą┐čĆąŠčüčéąĖčéčī ą┤ąŠčüčéčāą┐ ą║ čĆą░ąĘą╗ąĖčćąĮčŗą╝ čäčāąĮą║čåąĖčÅą╝ ą┤ąĄą╝ąŠąĮčüčéčĆą░čåąĖąŠąĮąĮąŠą│ąŠ ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ.
ą×čüąĮąŠą▓ąĮčŗąĄ čäčāąĮą║čåąĖąĖ čŹč鹊ą│ąŠ ą┐čĆąĖą╝ąĄčĆą░ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ FFT ą┤ą╗čÅ STM32F429:
ŌĆó ąōąĄąĮąĄčĆą░čåąĖčÅ čüąĖą│ąĮą░ą╗ą░ ą┤ą░ąĮąĮčŗčģ ąĖ ą┐ąĄčĆąĄą┤ą░čćą░ ąĄą│ąŠ č湥čĆąĄąĘ DMA1 Stream6 Channel7 ąĮą░ ą▓čŗčģąŠą┤ čåąĖčäčĆąŠ-ą░ąĮą░ą╗ąŠą│ąŠą▓ąŠą│ąŠ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░č鹥ą╗čÅ (DAC Channel2).
ŌĆó ąŚą░čģą▓ą░čé ą┤ą░ąĮąĮčŗčģ čüąĖą│ąĮą░ą╗ą░ čüąŠ ą▓čģąŠą┤ą░ ąÉą”ą¤ (ADC Channel0) ąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖąĄ ąĄą│ąŠ ą▓ ą┐ą░ą╝čÅčéčī č湥čĆąĄąĘ DMA2 Stream0 Channel0.
ŌĆó ąśąĘą╝ąĄąĮąĄąĮąĖąĄ čćą░čüč鹊čéčŗ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ čü ą┐ąŠą╝ąŠčēčīčÄ čéą░ą╣ą╝ąĄčĆą░ (ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ TIM2).
ŌĆó ąśąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ FFT čü čĆą░ąĘą╗ąĖčćąĮčŗą╝ąĖ ą┤ą░ąĮąĮčŗą╝ąĖ: Float-32, Q15 ąĖ Q31.
ŌĆó ąÆčŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ FFT ąĖ ą▓čŗčćąĖčüą╗ąĄąĮąĖąĄ ąĘąĮą░č湥ąĮąĖą╣ ą╝ą░ą│ąĮąĖčéčāą┤čŗ.
ŌĆó ą×č鹊ą▒čĆą░ąČąĄąĮąĖąĄ ą▓čģąŠą┤ąĮčŗčģ ąĖ ą▓čŗčģąŠą┤ąĮčŗčģ ą┤ą░ąĮąĮčŗčģ ąĮą░ 菹║čĆą░ąĮąĄ LCD.
ąöą╗čÅ STM32F746:
ŌĆó ąōąĄąĮąĄčĆą░čåąĖčÅ čüąĖą│ąĮą░ą╗ą░ ą┤ą░ąĮąĮčŗčģ ąĖ ą┐ąĄčĆąĄą┤ą░čćą░ ąĄą│ąŠ č湥čĆąĄąĘ DMA1 Stream5 Channel7 ąĮą░ ą▓čŗčģąŠą┤ čåąĖčäčĆąŠ-ą░ąĮą░ą╗ąŠą│ąŠą▓ąŠą│ąŠ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░č鹥ą╗čÅ (DAC Channel1).
ŌĆó ąŚą░čģą▓ą░čé ą┤ą░ąĮąĮčŗčģ čüąĖą│ąĮą░ą╗ą░ čüąŠ ą▓čģąŠą┤ą░ ąÉą”ą¤ (ADC Channel4) ąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖąĄ ąĄą│ąŠ ą▓ ą┐ą░ą╝čÅčéčī č湥čĆąĄąĘ DMA2 Stream0 Channel0.
ŌĆó ąśąĘą╝ąĄąĮąĄąĮąĖąĄ čćą░čüč鹊čéčŗ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ čü ą┐ąŠą╝ąŠčēčīčÄ čéą░ą╣ą╝ąĄčĆą░ (ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ TIM2).
ŌĆó ąśąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ FFT čü čĆą░ąĘą╗ąĖčćąĮčŗą╝ąĖ ą┤ą░ąĮąĮčŗą╝ąĖ: Float-32, Q15 ąĖ Q31.
ŌĆó ąÆčŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ FFT ąĖ ą▓čŗčćąĖčüą╗ąĄąĮąĖąĄ ąĘąĮą░č湥ąĮąĖą╣ ą╝ą░ą│ąĮąĖčéčāą┤čŗ.
ŌĆó ą×č鹊ą▒čĆą░ąČąĄąĮąĖąĄ ą▓čģąŠą┤ąĮčŗčģ ąĖ ą▓čŗčģąŠą┤ąĮčŗčģ ą┤ą░ąĮąĮčŗčģ ąĮą░ 菹║čĆą░ąĮąĄ LCD.
ą×č湥ą▓ąĖą┤ąĮąŠ, čćč鹊 ą┐ąŠ čäčāąĮą║čåąĖąŠąĮą░ą╗čā čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ STM32F429 ąĖ STM32F746 čüąŠą▓ą┐ą░ą┤ą░čÄčé, ąĖ ą▒ąĖą▒ą╗ąĖąŠč鹥ą║ą░ CMSIS ą║ą░ą║ čĆą░ąĘ ąĖ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čüąĮąĖąČąĄąĮąĖąĄ ąĘą░čéčĆą░čé ąĮą░ ą┐ąŠčĆčéąĖčĆąŠą▓ą░ąĮąĖąĄ ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ čü ąŠą┤ąĮąŠą│ąŠ MCU ąĮą░ ą┤čĆčāą│ąŠą╣.
ąÜčāčüąŠą║ ą║ąŠą┤ą░ ąĮąĖąČąĄ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé, ą║ą░ą║ ąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░čéčī čäčāąĮą║čåąĖčÄ CFFT ą┤ą╗čÅ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ FFT ąĮą░ 1024, 256 ąĖą╗ąĖ 64 č鹊čćą║ąĖ, ąĖ ą▓čŗą┐ąŠą╗ąĮąĖčéčī ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ ą▓čģąŠą┤ąĮčŗčģ čüąĖą│ąĮą░ą╗ąŠą▓ (aFFT_Input_f32) ąĖąĘ ą┤ąŠą╝ąĄąĮą░ ą▓čĆąĄą╝ąĄąĮąĖ ą▓ ą┤ąŠą╝ąĄąĮ čćą░čüč鹊čéčŗ, ą┐ąŠčüą╗ąĄ č湥ą│ąŠ ą▓čŗčćąĖčüą╗čÅąĄčéčüčÅ ą╝ą░ą│ąĮąĖčéčāą┤ą░ ą║ą░ąČą┤ąŠą│ąŠ ą▒ąĖąĮą░, ąĖ ą▓ ąĘą░ą▓ąĄčĆčłąĄąĮąĖąĄ ą▓čŗčćąĖčüą╗čÅąĄčéčüčÅ ąĖ ą▓ąŠąĘą▓čĆą░čēą░ąĄčéčüčÅ ąĘąĮą░č湥ąĮąĖąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠą╣ ą╝ą░ą│ąĮąĖčéčāą┤čŗ.
// ąśąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÅ ą╝ąŠą┤čāą╗čÅ CFFT/CIFFT, intFlag=0, doBitReverse=1:
arm_cfft_radix4_init_f32(&FFT_F32_struct,
FFT_Length,
FFT_INVERSE_FLAG,
FFT_Normal_OUTPUT_FLAG);
// ążčāąĮą║čåąĖčÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ą┤ą╗čÅ floating-point Radix-4 CFFT/CIFFT:
arm_cfft_radix4_f32(&FFT_F32_struct, aFFT_Input_f32);
// ą×ą▒čĆą░ą▒ąŠčéą║ą░ ą┤ą░ąĮąĮčŗčģ čü ą┐ąŠą╝ąŠčēčīčÄ Complex Magnitude Module,
// ą┤ą╗čÅ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą╝ą░ą│ąĮąĖčéčāą┤čŗ ą║ą░ąČą┤ąŠą│ąŠ ą▒ąĖąĮą░:
arm_cmplx_mag_f32(aFFT_Input_f32, aFFT_Output_f32, FFT_Length);
// ąÆčŗčćąĖčüą╗ąĄąĮąĖąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ maxValue:
arm_max_f32(aFFT_Output_f32, FFT_Length, &maxValue, &maxIndex);
ąŚąĮą░č湥ąĮąĖąĄ FFT_Length ąĘą░ą▓ąĖčüąĖčé ąŠčé ą▓čŗą▒ąŠčĆą░ ą┐ąŠą╗čīąĘąŠą▓ą░č鹥ą╗čÅ, ąŠąĮąŠ ą╝ąŠąČąĄčé ą▒čŗčéčī 1024, 256 ąĖą╗ąĖ 64. ąśąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÄ FFT ąĖ ąŠą▒čĆą░ą▒ąŠčéą║čā ą┤čĆčāą│ąĖčģ č乊čĆą╝ą░č鹊ą▓ ą╝ąŠąČąĮąŠ ąĮą░ą╣čéąĖ ą▓ ąĖčüčģąŠą┤ąĮąŠą╝ čäą░ą╣ą╗ąĄ fft_processing.c.
[ą¤čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéčī FFT]
ąĀąĖčü. 4 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ą▓čĆąĄą╝čÅ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ ąĖ ą║ąŠą╗ąĖč湥čüčéą▓ąŠ čéą░ą║č鹊ą▓ čĆą░čüč湥čéą░ FFT ąĮą░ STM32F429, čĆą░ą▒ąŠčéą░čÄčēąĄą╝ ąĮą░ čćą░čüč鹊č鹥 180 ą£ąōčå, ą▓ č鹊 ą▓čĆąĄą╝čÅ ą║ą░ą║ čĆąĖčü. 5 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čĆąĄąĘčāą╗čīčéą░čé čü č鹥ą╝ąĖ ąČąĄ ą┐ą░čĆą░ą╝ąĄčéčĆą░ą╝ąĖ, ąĖąĘą╝ąĄčĆąĄąĮąĮčŗą╣ ąĮą░ STM32F746, čĆą░ą▒ąŠčéą░čÄčēąĄą╝ ąĮą░ čćą░čüč鹊č鹥 216 ą£ąōčå. ą×ą▒ą░ ą┐čĆąĖą╝ąĄčĆą░ ą║ąŠą┤ą░ ą▒čŗą╗ąĖ čüąŠą▒čĆą░ąĮčŗ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čéčāą╗č湥ą╣ąĮą░ MDK-ArmŌäó (5.14.0.0) čü ą┐ąŠą┤ą┤ąĄčƹȹ║ąŠą╣ ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆą░ čÅąĘčŗą║ą░ C V5.05, čü ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĄą╣ Level 3 (-O3) ą┤ą╗čÅ ą▓čĆąĄą╝ąĄąĮąĖ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ.

ąĀąĖčü. 4. ą¤čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéčī ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ čĆą░ąĘą╝ąĄčĆą░ FFT ąĮą░ STM32F429.

ąĀąĖčü. 5. ą¤čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéčī ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ čĆą░ąĘą╝ąĄčĆą░ FFT ąĮą░ STM32F746.
ąĀą░ą▒ąŠčéą░ ą║ąŠą┤ą░ ąĮą░ STM32F429I-DISCO. ą¦č鹊ą▒čŗ ąĘą░ą┐čāčüčéąĖčéčī ąŠą┤ąĖąĮ ąĖąĘ ą▓čŗą▒čĆą░ąĮąĮčŗčģ ą┐čĆąĖą╝ąĄčĆąŠą▓ FFT, ą┐ąŠą┤ą║ą╗čÄčćąĖč鹥 PA5 ą║ PA0. ążąŠčĆą╝ą░ ąĖ čüą┐ąĄą║čéčĆ čüąĖą│ąĮą░ą╗ą░ ą▒čāą┤ąĄčé ąŠč鹊ą▒čĆą░ąČąĄąĮą░ ąĮą░ LCD.
ąśąĘą╝ąĄąĮąĄąĮąĖąĄą╝ ą┐ąŠąĘąĖčåąĖąĖ čüą╗ą░ą╣ą┤ąĄčĆą░ ąÆčŗ ą╝ąŠąČąĄč鹥 ąĮą░ą▒ą╗čÄą┤ą░čéčī č乊čĆą╝čā ąĮąŠą▓ąŠą│ąŠ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ ąĖ ąĄą│ąŠ čüą┐ąĄą║čéčĆ, ąŠą▒ąĮąŠą▓ą╗čÅčÄčēąĖąĄčüčÅ ą▓ čĆąĄą░ą╗čīąĮąŠą╝ ą▓čĆąĄą╝ąĄąĮąĖ (čüą╝. čĆąĖčü. 6).

ąĀąĖčü. 6. ąŚą░ą┐čāčüą║ FFT ąĮą░ 1024 č鹊čćą║ąĖ čü ą▓čģąŠą┤ąĮčŗą╝ąĖ ą┤ą░ąĮąĮčŗą╝ąĖ Float-32 ąĮą░ ąŠčåąĄąĮąŠčćąĮąŠą╣ ą┐ą╗ą░č鹥 čĆą░ąĘčĆą░ą▒ąŠčéčćąĖą║ą░ STM32F429I-DISCO.
ąĀą░ą▒ąŠčéą░ ą║ąŠą┤ą░ ąĮą░ STM32F746-DISCO. ąÆ čŹč鹊ą╝ čüą╗čāčćą░ąĄ ą╝ąŠąČąĮąŠ ąŠčåąĄąĮąĖčéčī ą┤ąŠčüč鹊ąĖąĮčüčéą▓ą░ čüčāčēąĄčüčéą▓čāčÄčēąĄą│ąŠ čüąŠąĄą┤ąĖąĮąĄąĮąĖčÅ ą╝ąĄąČą┤čā PA4 ąĖ DCMI_HSYNC. ąöčĆčāą│ąĖąĄ čüąŠąĄą┤ąĖąĮąĄąĮąĖąĄ ąĮąĄ ąĮčāąČąĮčŗ, ą┐ąŠčüą║ąŠą╗čīą║čā ą┐ąŠčĆčé PA4 čüą║ąŠąĮčäąĖą│čāčĆąĖčĆąŠą▓ą░ąĮ ą║ą░ą║ ą▓čŗčģąŠą┤ DAC1 ąĖ ą▓čģąŠą┤ ADC1. ążąŠčĆą╝ą░ ąĖ čüą┐ąĄą║čéčĆ čüąĖą│ąĮą░ą╗ą░ ąŠč鹊ą▒čĆą░ąČą░čÄčéčüčÅ ąĮą░ LCD.
ąśąĘą╝ąĄąĮąĄąĮąĖąĄą╝ ą┐ąŠąĘąĖčåąĖąĖ čüą╗ą░ą╣ą┤ąĄčĆą░ ą┐ąŠą╗čīąĘąŠą▓ą░č鹥ą╗čī ą╝ąŠąČąĄčé čāą▓ąĖą┤ąĄčéčī č乊čĆą╝čā ąĮąŠą▓ąŠą│ąŠ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ ąĖ ąĄą│ąŠ čüą┐ąĄą║čéčĆ, ąŠą▒ąĮąŠą▓ą╗čÅčÄčēąĖąĄčüčÅ ą▓ čĆąĄą░ą╗čīąĮąŠą╝ ą▓čĆąĄą╝ąĄąĮąĖ (čüą╝. čĆąĖčü. 7).
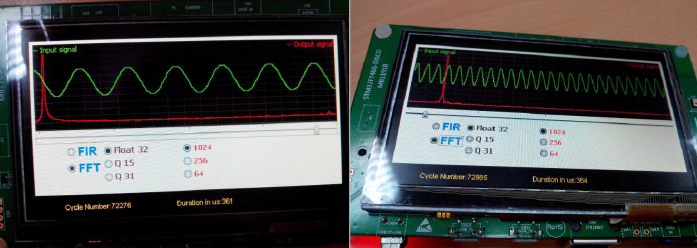
ąĀąĖčü. 7. ąŚą░ą┐čāčüą║ FFT ąĮą░ 1024 č鹊čćą║ąĖ čü ą▓čģąŠą┤ąĮčŗą╝ąĖ ą┤ą░ąĮąĮčŗą╝ąĖ Float-32 ąĮą░ ąŠčåąĄąĮąŠčćąĮąŠą╣ ą┐ą╗ą░č鹥 čĆą░ąĘčĆą░ą▒ąŠčéčćąĖą║ą░ STM32F746-DISCO.
ą”ąĄą╗čī čŹč鹊ą╣ ą┤ąĄą╝ąŠąĮčüčéčĆą░čåąĖąĖ - čāčüčéčĆą░ąĮąĖčéčī čüąĖą│ąĮą░ą╗ ą┐ąŠą╝ąĄčģąĖ (čüąĖąĮčāčüąŠąĖą┤ą░ą╗čīąĮčŗą╣ čüąĖą│ąĮą░ą╗ 15 ą║ąōčå) ąĖąĘ ąČąĄą╗ą░ąĄą╝ąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ (čüąĖąĮčāčüąŠąĖą┤ą░ą╗čīąĮčŗą╣ čüąĖą│ąĮą░ą╗ 1 ą║ąōčå), ąĮą░ą╗ąŠąČąĖą▓ ąĮą░ ą▓čģąŠą┤ąĮčŗąĄ ą┤ą░ąĮąĮčŗąĄ čĆą░ąĘąĮąŠą│ąŠ č乊čĆą╝ą░čéą░ ążąØą¦ FIR. ąÜąŠą│ą┤ą░ ą▓čŗą▒ąĖčĆą░ąĄčéčüčÅ č乊čĆą╝ą░čé Q15, ą╝ąŠąČąĮąŠ ąĖąĘąŠą╗ąĖčĆąŠą▓ą░čéčī čüąĖą│ąĮą░ą╗ ą┐ąŠą╝ąĄčģąĖ, ą┐čĆąĖą╝ąĄąĮąĖą▓ ążąÆą¦ FIR.
ąæą╗ąŠą║-čüčģąĄą╝ą░ ą┐čĆąĖą╝ąĄčĆą░ FIR ą┐ąŠą║ą░ąĘą░ąĮą░ ąĮą░ čĆąĖčü. 8.

ąĀąĖčü. 8. ąæą╗ąŠą║-čüčģąĄą╝ą░ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ FIR-čäąĖą╗čīčéčĆą░.
ąÜąŠą┤ ąĮąĖąČąĄ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÄ ą┤ą╗čÅ FIR-čäąĖą╗čīčéčĆą░ ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąĖ (floating-point) ąĖ ąĄą│ąŠ čäčāąĮą║čåąĖčÄ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ.
// ąÆčŗąĘąŠą▓ čäčāąĮą║čåąĖąĖ ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖąĖ FIR, ą║ąŠč鹊čĆą░čÅ ąĘą░ą┐ąŠą╗ąĮčÅąĄčé ą┐ąŠą╗čÅ
// 菹║ąĘąĄą╝ą┐ą╗čÅčĆą░ čüčéčĆčāą║čéčāčĆčŗ čäąĖą╗čīčéčĆą░:
arm_fir_init_f32(&FIR_F32_Struct,
NUM_TAPS,
(float32_t *)&aFIR_F32_Coeffs[0],
&firStateF32[0],
blockSize);
for(counter_FIR_f32_p=0; counter_FIR_f32_p=0 < numBlocks; counter_FIR_f32_p++)
{
arm_fir_f32(&FIR_F32_Struct,
aFIR_F32_1kHz_15kHz + (counter_FIR_f32_p * blockSize),
aFIR_F32_Output + (counter_FIR_f32_p * blockSize),
blockSize);
}
ąśąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÄ FIR ąĖ ąŠą▒čĆą░ą▒ąŠčéą║čā ą┤čĆčāą│ąĖčģ č乊čĆą╝ą░č鹊ą▓ ą╝ąŠąČąĮąŠ ąĮą░ą╣čéąĖ ą▓ ąĖčüčģąŠą┤ąĮąŠą╝ čäą░ą╣ą╗ąĄ fir_processing.c.
ąÆčģąŠą┤ąĮčŗąĄ ą┤ą░ąĮąĮčŗąĄ ą┤ą╗čÅ FIR-čäąĖą╗čīčéčĆą░ čŹč鹊 čüčāą╝ą╝ą░ čüąĖąĮčāčüąŠąĖą┤ 1 ą║ąōčå ąĖ 15 ą║ąōčå (čüą╝. čĆąĖčü. 9), ą║ąŠč鹊čĆą░čÅ ą▒čŗą╗ą░ čüą│ąĄąĮąĄčĆąĖčĆąŠą▓ą░ąĮą░ ą▓ čüčĆąĄą┤ąĄ MATLAB┬« ą▓ č乊čĆą╝ą░č鹥 ą┤ą░ąĮąĮčŗčģ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąŠą╣. ąöą╗čÅ čŹč鹊ą╣ čåąĄą╗ąĖ ą┐čĆąĖą╝ąĄąĮčÅą╗čüčÅ ą┐čĆąŠčüč鹊ą╣ čüą║čĆąĖą┐čé [4]:
% ąÜąŠą╗ąĖč湥čüčéą▓ąŠ ą▓čŗą▒ąŠčĆąŠą║ ą▓ čüąĄą║čāąĮą┤čā:
Fs = 48000;% ą¤ąĄčĆąĖąŠą┤:
T = 1/Fs;
% ąÜąŠą╗ąĖč湥čüčéą▓ąŠ ą▓čŗą▒ąŠčĆąŠą║ ą▓ čüąĖą│ąĮą░ą╗ąĄ:
Length=320;
t=(0:Length-1)*T;
% ąōąĄąĮąĄčĆą░čåąĖčÅ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░:
Input_signal = sin(2*pi*1000*t) + 0.5*sin(2*pi*15000*t);
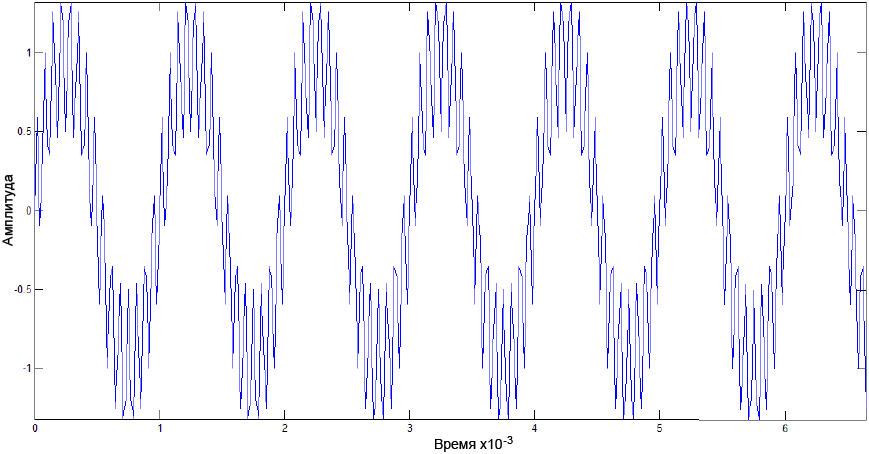
ąĀąĖčü. 9. ąĪą│ąĄąĮąĄčĆąĖčĆąŠą▓ą░ąĮąĮčŗą╣ ą▓čģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗ (čüčāą╝ą╝ą░ ą┤ą▓čāčģ čüąĖąĮčāčüąŠąĖą┤ 1 ą║ąōčå ąĖ 15 ą║ąōčå).
ą£ą░ą│ąĮąĖčéčāą┤ą░ čüą┐ąĄą║čéčĆą░ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ (čĆąĖčü. 10) ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé 2 čćą░čüč鹊čéčŗ 1 ą║ąōčå ąĖ 15 ą║ąōčå.
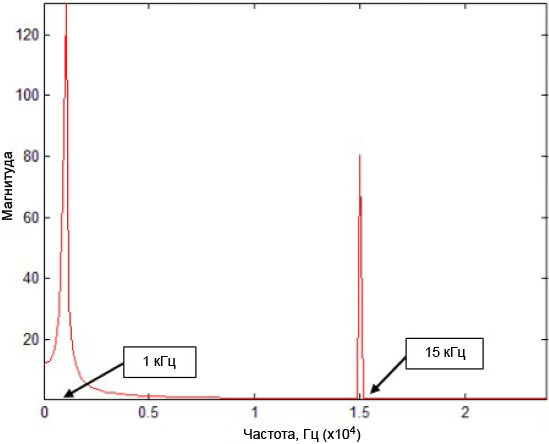
ąĀąĖčü. 10. ą£ą░ą│ąĮąĖčéčāą┤čŗ čüą┐ąĄą║čéčĆą░ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░.
ą¤ąŠčüą║ąŠą╗čīą║čā čłčāą╝ ą┐ąŠąĘąĖčåąĖąŠąĮąĖčĆčāąĄčéčüčÅ ą▓ čüą┐ąĄą║čéčĆąĄ ąŠą║ąŠą╗ąŠ 15 ą║ąōčå, čćą░čüč鹊čéą░ čüčĆąĄąĘą░ ą┤ąŠą╗ąČąĮą░ ą▒čŗčéčī čāčüčéą░ąĮąŠą▓ą╗ąĄąĮą░ ąĮą░ čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĄą╣ ą▒ąŠą╗ąĄąĄ ąĮąĖąĘą║ąŠą╣ čćą░čüč鹊č鹥, ąĮą░ą┐čĆąĖą╝ąĄčĆ ąĮą░ 6 ą║ąōčå.
ąöąĖąĘą░ą╣ąĮ FIR-čäąĖą╗čīčéčĆą░. ą×čüąĮąŠą▓ąĮčŗąĄ čäčāąĮą║čåąĖąĖ čäąĖą╗čīčéčĆą░ ą┐ąĄčĆąĄčćąĖčüą╗ąĄąĮčŗ ą▓ čéą░ą▒ą╗ąĖčåąĄ 4.
ąóą░ą▒ą╗ąĖčåą░ 4. ą¤ą░čĆą░ą╝ąĄčéčĆčŗ FIR-čäąĖą╗čīčéčĆą░.
| ążčāąĮą║čåąĖčÅ/ą┐ą░čĆą░ą╝ąĄčéčĆ |
ąŚąĮą░č湥ąĮąĖąĄ |
| ąóąĖą┐ čäąĖą╗čīčéčĆą░ |
Low-pass (ążąØą¦) |
| ą¤ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ |
28 |
| ą¦ą░čüč鹊čéą░ ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ |
48 ą║ąōčå |
| ą¦ą░čüč鹊čéą░ čüčĆąĄąĘą░ |
6 ą║ąōčå |
ążąØą¦ ą▒čŗą╗ čĆą░čüčüčćąĖčéą░ąĮ čéą░ą║ąČąĄ čü ą┐ąŠą╝ąŠčēčīčÄ MATLAB┬«, čüą╗ąĄą┤čāčÄčēąĖą╝ąĖ ą║ąŠą╝ą░ąĮą┤ą░ą╝ąĖ:
% ą×ą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ čćą░čüč鹊čéčŗ čüčĆąĄąĘą░ čäąĖą╗čīčéčĆą░:
Cutoff_Freq = 6000;
% ą¦ą░čüč鹊čéą░ ąØą░ą╣ą║ą▓ąĖčüčéą░:
Nyq_Freq = Fs/2;
cutoff_norm = Cutoff_Freq / Nyq_Freq;
% ą¤ąŠčĆčÅą┤ąŠą║ FIR-čäąĖą╗čīčéčĆą░:
order = 28;
% ąĪąŠąĘą┤ą░ąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ ążąØą¦ FIR:
FIR_Coeff = firl(order, cutoff_norm);
% ążąĖą╗čīčéčĆą░čåąĖčÅ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ FIR-čäąĖą╗čīčéčĆąŠą╝:
Filtered_signal = filter(FIR_Coeff, 1, Input_signal);
ą¤čĆąĖą╝ąĄčćą░ąĮąĖąĄ: ą┐ąŠčĆčÅą┤ąŠą║ FIR-čäąĖą╗čīčéčĆą░ čĆą░ą▓ąĄąĮ ą║ąŠą╗ąĖč湥čüčéą▓čā ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ - 1.
ą¦č鹊ą▒čŗ ą┐čĆąŠą▓ąĄčĆąĖčéčī čĆą░ąĘčĆą░ą▒ąŠčéą░ąĮąĮčŗą╣ čäąĖą╗čīčéčĆ, ą╝ąŠąČąĮąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī ąĖąĮčüčéčĆčāą╝ąĄąĮčé ą▓ąĖąĘčāą░ą╗ąĖąĘą░čåąĖąĖ ą┤ą░ąĮąĮčŗčģ (Visualization Tool) ą▓ MATLAB┬« čü ą┐ąŠą╝ąŠčēčīčÄ čüą╗ąĄą┤čāčÄčēąĄą╣ ą║ąŠą╝ą░ąĮą┤čŗ:
fvtool(FIR_Coeff, 'Fs', Fs);
ąśąĮčüčéčĆčāą╝ąĄąĮčé Filter Visualization Tool (FVT) čŹč鹊 ą┐čĆą░ą║čéąĖč湥čüą║ąŠąĄ čüčĆąĄą┤čüčéą▓ąŠ ą┐čĆąŠą▓ąĄčĆą║ąĖ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ čüąŠą▒čĆą░ąĮąĮąŠą│ąŠ čäąĖą╗čīčéčĆą░. ąØą░ čĆąĖčü. 11 ą┐ąŠą║ą░ąĘą░ąĮčŗ čüą╗ąĄą┤čāčÄčēąĖąĄ ą┤ą░ąĮąĮčŗąĄ (čüą▓ąĄčĆčģčā ą▓ąĮąĖąĘ):
ŌĆó Magnitude response (ąÉą¦ąź čäąĖą╗čīčéčĆą░).
ŌĆó ąŻčüąĖą╗ąĄąĮąĖąĄ čäąĖą╗čīčéčĆą░ (ą▓ dB) ą▓ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ ąŠčé čćą░čüč鹊čéčŗ (ą▓ ąōčå).
ŌĆó Impulse response (ąŠčéą▓ąĄčé ąĮą░ ąŠą┤ąĖąĮąŠčćąĮčŗą╣ ąĖą╝ą┐čāą╗čīčü).
ŌĆó Step response (ąŠčéą▓ąĄčé ąĮą░ ą┐ąĄčĆąĄą┐ą░ą┤ čāčĆąŠą▓ąĮčÅ).

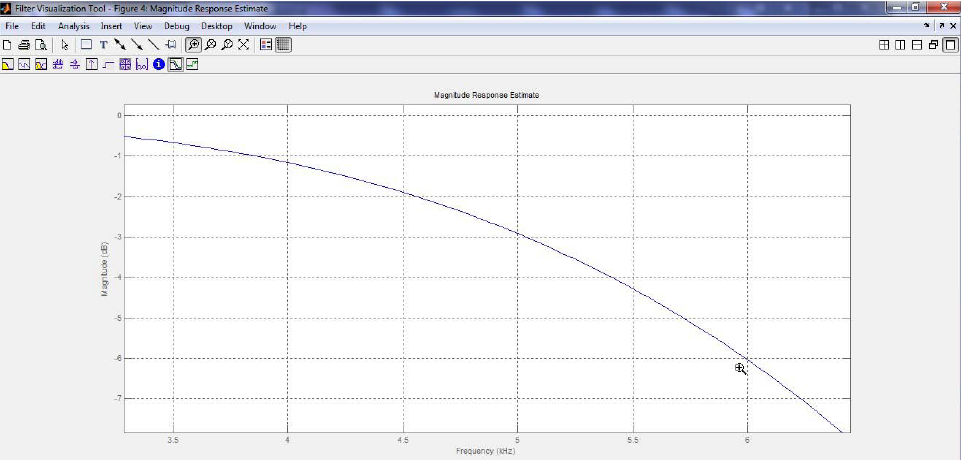
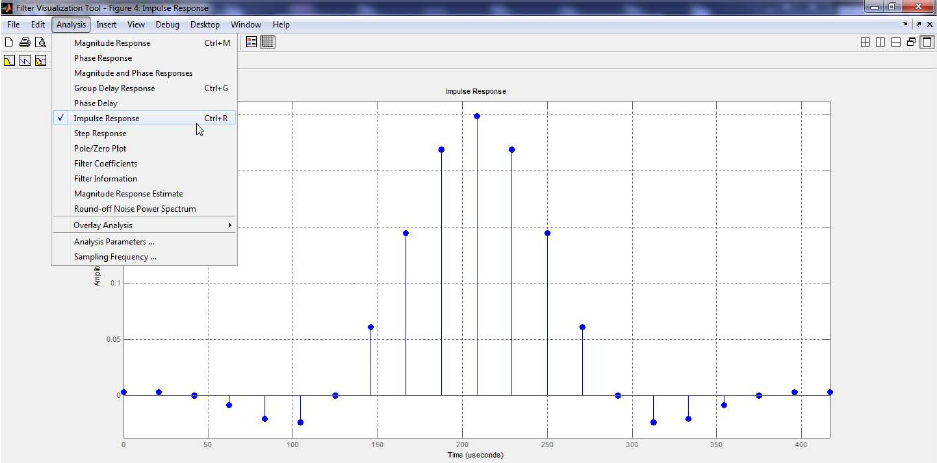

ąĀąĖčü. 11. ą¤čĆąŠą▓ąĄčĆą║ą░ FIR-čäąĖą╗čīčéčĆą░ čü ą┐ąŠą╝ąŠčēčīčÄ ąĖąĮčüčéčĆčāą╝ąĄąĮčéą░čĆąĖčÅ MATLAB┬« FVT.
ą¤čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéčī FIR-čäąĖą╗čīčéčĆą░. ąĀąĖčü. 12 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ą▓čĆąĄą╝čÅ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ ąĖ ą║ąŠą╗ąĖč湥čüčéą▓ąŠ ą┐ąŠčéčĆą░č湥ąĮąĮčŗčģ čéą░ą║č鹊ą▓ ąĮą░ ą┐čĆąŠčüč湥čé čĆą░ąĘčĆą░ą▒ąŠčéą░ąĮąĮąŠą│ąŠ ą▓čŗčłąĄ FIR-čäąĖą╗čīčéčĆą░ ąĮą░ STM32F429I, čĆą░ą▒ąŠčéą░čÄčēąĄą╝ ąĮą░ čćą░čüč鹊č鹥 180 ą£ąōčå, ą▓ č鹊 ą▓čĆąĄą╝čÅ ą║ą░ą║ čĆąĖčü. 13 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čĆąĄąĘčāą╗čīčéą░čé čĆą░ą▒ąŠčéčŗ STM32F746, čĆą░ą▒ąŠčéą░čÄčēąĄą│ąŠ ąĮą░ čćą░čüč鹊č鹥 216 ą£ąōčå. ą×ą▒ą░ ą┐čĆąĖą╝ąĄčĆą░ ą║ąŠą┤ą░ ą▒čŗą╗ąĖ čüąŠą▒čĆą░ąĮčŗ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čéčāą╗č湥ą╣ąĮą░ MDK-ArmŌäó (5.14.0.0) čü ą┐ąŠą┤ą┤ąĄčƹȹ║ąŠą╣ ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆą░ čÅąĘčŗą║ą░ C V5.05, čü ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĄą╣ Level 3 (-O3) ą┤ą╗čÅ ą▓čĆąĄą╝ąĄąĮąĖ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ.
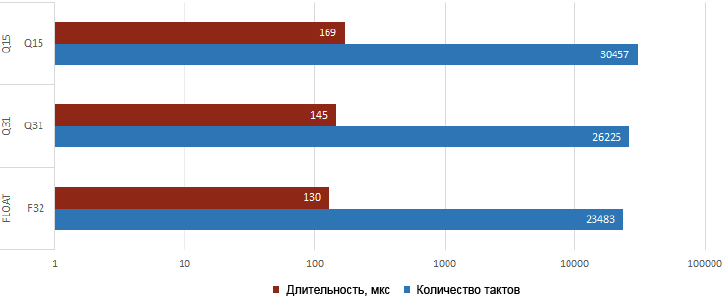
ąĀąĖčü. 12. ą¤čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéčī ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ FIR-čäąĖą╗čīčéčĆą░ ąĮą░ STM32F429.

ąĀąĖčü. 13. ą¤čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéčī ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ FIR-čäąĖą╗čīčéčĆą░ ąĮą░ STM32F746.
ą×ą▒ąĘąŠčĆ ą┐čĆąĖą╝ąĄčĆą░ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ FIR-čäąĖą╗čīčéčĆą░. ą×čüąĮąŠą▓ąĮčŗąĄ čäčāąĮą║čåąĖąĖ ą┐čĆąĖą╝ąĄčĆą░ čüą╗ąĄą┤čāčÄčēąĖąĄ:
ŌĆó ąōąĄąĮąĄčĆąĖčĆčāčÄčéčüčÅ ą┤ą░ąĮąĮčŗąĄ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░, ąĖ ąŠąĮąĖ čüąŠčģčĆą░ąĮčÅčÄčéčüčÅ ą▓ RAM.
ŌĆó ąśąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆčāąĄčéčüčÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░ FFT ą┤ą╗čÅ čĆą░ąĘą╗ąĖčćąĮčŗčģ čéąĖą┐ąŠą▓ ą┤ą░ąĮąĮčŗčģ: Float-32, Q15 ąĖ Q31.
ŌĆó ą¤čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ ążąØą¦ FIR ą┤ą╗čÅ Float-32, Q15 ąĖ Q31.
ŌĆó ą¤čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ ążąÆą¦ FIR ą┤ą╗čÅ Q15.
ŌĆó ąÆčģąŠą┤ąĮčŗąĄ ąĖ ą▓čŗčģąŠą┤ąĮčŗąĄ ą┤ą░ąĮąĮčŗąĄ ąŠč鹊ą▒čĆą░ąČą░čÄčéčüčÅ ąĮą░ 菹║čĆą░ąĮąĄ LCD.
ąĀąĄąĘčāą╗čīčéą░čéčŗ ąĮą░ STM32F429I-DISCO. ąŁč鹊čé ą┐čĆąĖą╝ąĄčĆ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄčé 2 čüčåąĄąĮą░čĆąĖčÅ:
1. ążąØą¦ FIR, ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░čÄčēąĖą╣ č乊čĆą╝ą░čéčŗ ą┤ą░ąĮąĮčŗčģ Float-32, Q31 ąĖ Q15.
2. ążąÆą¦ FIR, ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░čÄčēąĖą╣ č鹊ą╗čīą║ąŠ č乊čĆą╝ą░čé ąĖ Q15.
ąŁą║čĆą░ąĮ ąŠčüčåąĖą╗ą╗ąŠą│čĆą░čäą░ ąĘą░čģą▓ą░čéčŗą▓ą░ąĄčé 3 čĆą░ąĘąĮčŗąĄ ą║ąŠąĮčäąĖą│čāčĆą░čåąĖąĖ, čćč鹊 ą┐ąŠą║ą░ąĘą░ąĮąŠ ąĮą░ čĆąĖčü. 14, čüą╗ąĄą▓ą░ ąĮą░ą┐čĆą░ą▓ąŠ:
1. ążąØą¦ FIR ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ ą▓ č乊čĆą╝ą░č鹥 ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ ąĘą░ą┐čÅč鹊ą╣ (Float-32).
2. ążąØą¦ FIR ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ ą▓ č乊čĆą╝ą░č鹥 Q15.
3. ążąÆą¦ FIR ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ ą▓ č乊čĆą╝ą░č鹥 Q15.
ąĀąĄąĘčāą╗čīčéą░čéčŗ ąĮą░ STM32F746-DISCO. ąóąŠčé ąČąĄ čüą░ą╝čŗą╣ ą┐čĆąĖą╝ąĄčĆ FIR-čäąĖą╗čīčéčĆąŠą▓, čĆąĄąĘčāą╗čīčéą░čéčŗ ą┐ąŠą║ą░ąĘą░ąĮčŗ ąĮą░ čĆąĖčü. 15, čüą╗ąĄą▓ą░ ąĮą░ą┐čĆą░ą▓ąŠ:
1. ążąØą¦ FIR ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ ą▓ č乊čĆą╝ą░č鹥 ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ ąĘą░ą┐čÅč鹊ą╣ (Float-32).
2. ążąØą¦ FIR ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ ą▓ č乊čĆą╝ą░č鹥 Q15.
3. ążąÆą¦ FIR ą┐čĆąĖ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ ą▓ č乊čĆą╝ą░č鹥 Q15.
[ą×ą▒ąĘąŠčĆ DSP-ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéąĖ STM32]
ą×ą┤ąĮąŠ ąĖąĘ ąĮą░ąĘąĮą░č湥ąĮąĖą╣ čŹč鹊ą│ąŠ ą░ą┐ąĮąŠčāčéą░ - ą┐ąŠą║ą░ąĘą░čéčī čĆąĄąĘčāą╗čīčéą░čéčŗ č鹥čüčéąĖčĆąŠą▓ą░ąĮąĖčÅ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéąĖ ąĮą░ MCU čĆą░ąĘąĮčŗčģ čüąĄčĆąĖą╣ STM32. ą¤čĆąŠą▓ąĄčĆčÅą╗ąĖčüčī čüą╗ąĄą┤čāčÄčēąĖąĄ ą░ą╗ą│ąŠčĆąĖčéą╝čŗ:
ŌĆó ąÜąŠą╝ą┐ą╗ąĄą║čüąĮąŠąĄ FFT ą┐ąŠ 64 ąĖ 1024 č鹊čćą║ą░ą╝ (radix-4).
ŌĆó ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ č乊čĆą╝ą░č鹊ą▓ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ (Q15 ąĖ Q31).
ąĪčĆą░ą▓ąĮąĄąĮąĖąĄ ąŠčüčāčēąĄčüčéą▓ą╗čÅą╗ąŠčüčī ą┐ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ (čé. ąĄ. čüą║ąŠą╗čīą║ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ąĘą░ą╣ą╝ąĄčé ąŠą▒čĆą░ą▒ąŠčéą║ą░ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ FFT). ąÆčģąŠą┤ąĮąŠą╣ ą▓ąĄą║č鹊čĆ ą┤ą░ąĮąĮčŗčģ ą▒čŗą╗ čüą│ąĄąĮąĄčĆąĖčĆąŠą▓ą░ąĮ ą▓ MATLAB┬« čüą╗ąĄą┤čāčÄčēąĖą╝ąĖ ą║ąŠą╝ą░ąĮą┤ą░ą╝ąĖ:
>> Fs=48000;
>> T=1/Fs;
>> L=1024;
>> t=(0:L-1)*T;
>> x = sin(2*pi*1000*t) + 0.5*sin(2*pi*15000*t);
>> x = x(:);
ąĀąĄąĘčāą╗čīčéą░čéčŗ čüą▓ąĄą┤ąĄąĮčŗ ą▓ čéą░ą▒ą╗ąĖčåčā 5. ąÜąŠą┤ ą║ąŠą╝ą┐ąĖą╗ąĖčĆąŠą▓ą░ą╗čüčÅ ą▓ čüčĆąĄą┤ąĄ čéčāą╗č湥ą╣ąĮą░ MDK-ArmŌäó (5.14.0.0) čü ą┐ąŠą┤ą┤ąĄčƹȹ║ąŠą╣ ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆą░ čÅąĘčŗą║ą░ C V5.05, čü ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĄą╣ Level 3 (-O3) ą┤ą╗čÅ ą▓čĆąĄą╝ąĄąĮąĖ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ.
ąóą░ą▒ą╗ąĖčåą░ 5. ą×čåąĄąĮą║ą░ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖč鹥ą╗čīąĮąŠčüčéąĖ FFT ąĮą░ čĆą░ąĘąĮčŗčģ ą╝ąŠą┤ąĄą╗čÅčģ MCU STM32.
| MCU |
SYSCLK, ą£ąōčå |
ą»ą┤čĆąŠ Cortex |
ążąŠčĆą╝ą░čé ą┤ą░ąĮąĮčŗčģ |
ąóąŠč湥ą║ FFT |
ą”ąĖą║ą╗ąŠą▓ |
ąÆčĆąĄą╝čÅ čĆą░čüč湥čéą░, ą╝ą║čü |
| STM32F091 |
48 |
M0 |
Q31 |
1024 |
783106 |
16314 |
| 64 |
26576 |
553 |
| Q15 |
1024 |
938278 |
19547 |
| 64 |
37522 |
781 |
| STM32F103 |
72 |
M3 |
Q31 |
1024 |
214098 |
2973 |
| 64 |
7983 |
110 |
| Q15 |
1024 |
248936 |
3457 |
| 64 |
9696 |
134 |
| STM32F217 |
120 |
M3 |
Q31 |
1024 |
193189 |
1609 |
| 64 |
6992 |
58 |
| Q15 |
1024 |
200608 |
1671 |
| 64 |
7828 |
65 |
| STM32F303 |
72 |
M4 |
Q31 |
1024 |
178005 |
2472 |
| 64 |
7129 |
99 |
| Q15 |
1024 |
101316 |
1407 |
| 64 |
4304 |
59 |
| STM32F429 |
180 |
M4 |
Q31 |
1024 |
153307 |
855 |
| 64 |
6025 |
33 |
| Q15 |
1024 |
82299 |
457 |
| 64 |
3655 |
20 |
| STM32F746 |
216 |
M7 |
Q31 |
1024 |
93725 |
468 |
| 64 |
4537 |
22 |
| Q15 |
1024 |
56989 |
284 |
| 64 |
2994 |
14 |
| STM32L073 |
32 |
M0+ |
Q31 |
64 |
33493 |
1046 |
| Q15 |
64 |
44506 |
1390 |
| STM32L476 |
80 |
M4 |
Q31 |
1024 |
144214 |
1802 |
| 64 |
6007 |
75 |
| Q15 |
1024 |
77371 |
967 |
| 64 |
3509 |
43 |
[ąĪčüčŗą╗ą║ąĖ]
1. AN4841 Digital signal processing for STM32 microcontrollers using CMSIS site:st.com.
2. STM32: ą▒ą╗ąŠą║ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ č鹊čćą║ąŠą╣.
3. STM32F429 Discovery.
4. MATLAB: ą║ą░ą║ čüą│ąĄąĮąĄčĆąĖčĆąŠą▓ą░čéčī čüąĖą│ąĮą░ą╗ ąĖ ąĄą│ąŠ čüą┐ąĄą║čéčĆ. |

ąÜąŠą╝ą╝ąĄąĮčéą░čĆąĖąĖ
RSS ą╗ąĄąĮčéą░ ą║ąŠą╝ą╝ąĄąĮčéą░čĆąĖąĄą▓ čŹč鹊ą╣ ąĘą░ą┐ąĖčüąĖ