|
ąÆ čüčéą░čéčīąĄ ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą┐ąŠčćčéąĖ ą┤ąŠčüą╗ąŠą▓ąĮčŗą╣ ą┐ąĄčĆąĄą▓ąŠą┤ ąĮą░ čĆčāčüčüą║ąĖą╣ čÅąĘčŗą║ ą░ą┐ąĮąŠčāčéą░ Atmel AVR223. ąĀą░čüčüą║ą░ąĘčŗą▓ą░ąĄčéčüčÅ, ą║ą░ą║ ąĮą░ ą┐čĆą░ą║čéąĖą║ąĄ čĆą░čüčüčćąĖčéą░čéčī ąĖ čüą┤ąĄą╗ą░čéčī čåąĖčäčĆąŠą▓ąŠą╣ čäąĖą╗čīčéčĆ ąĮą░ AVR. ąśčüčģąŠą┤ąĮąĖą║ąĖ ą┐čĆąĖą╝ąĄčĆąŠą▓ čäąĖą╗čīčéčĆąŠą▓ ą╝ąŠąČąĮąŠ čüą║ą░čćą░čéčī ą┐ąŠ čüčüčŗą╗ą║ąĄ [11].
[ąĪąŠą┤ąĄčƹȹ░ąĮąĖąĄ]
ŌĆó čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓
ŌĆó ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ ąĖ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ ą┤ą░ąĮąĮčŗčģ
ŌĆó ą▒čŗčüčéčĆą░čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ FIR-čäąĖą╗čīčéčĆą░ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
ŌĆó ą▒čŗčüčéčĆą░čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ IIR-čäąĖą╗čīčéčĆą░ 2-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
ŌĆó ą╝ąĄč鹊ą┤čŗ ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĖ
[1. ąÆą▓ąĄą┤ąĄąĮąĖąĄ]
ą¤čĆąĖą╗ąŠąČąĄąĮąĖčÅ, ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░čÄčēąĖąĄ čüąĖą│ąĮą░ą╗čŗ ąŠčé ą▓ąĮąĄčłąĮąĖčģ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗčģ ąĖčüč鹊čćąĮąĖą║ąŠą▓/čüąĄąĮčüąŠčĆąŠą▓ ąŠą▒čŗčćąĮąŠ ąĮčāąČą┤ą░čÄčéčüčÅ ą▓ ąĮąĄą║ąŠč鹊čĆąŠą╣ čåąĖčäčĆąŠą▓ąŠą╣ čäąĖą╗čīčéčĆą░čåąĖąĖ. ąöą╗čÅ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą▓čŗčüąŠą║ąŠą│ąŠ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ čäąĖą╗čīčéčĆą░ ąŠą▒čŗčćąĮąŠ ą▓čŗą▒ąĖčĆą░čÄčé čüą┐ąĄčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮąĮčŗąĄ ą”ąĖčäčĆąŠą▓čŗąĄ ąĪąĖą│ąĮą░ą╗čīąĮčŗąĄ ą¤čĆąŠčåąĄčüčüąŠčĆčŗ (Digital Signal Processors, DSP), ąĮąŠ ą▓ąŠ ą╝ąĮąŠą│ąĖčģ čüą╗čāčćą░čÅčģ ąŠąĮąĖ ąŠą║ą░ąĘčŗą▓ą░čÄčéčüčÅ čüą╗ąĖčłą║ąŠą╝ ą┤ąŠčĆąŠą│ąĖą╝ąĖ ą┤ą╗čÅ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ. ąÆ čŹč鹊ą╝ čüą╗čāčćą░ąĄ ąĮą░ čüčåąĄąĮčā ą▓čŗčģąŠą┤čÅčé 8- ąĖ 16-ą▒ąĖčéąĮčŗąĄ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆčŗ (MCU). ą×ąĮąĖ ąĮąĄą┤ąŠčĆąŠą│ąĖ, čŹčäč乥ą║čéąĖą▓ąĮčŗ, ąĖ ąĖą╝ąĄčÄčé ą▓čüąĄ ą▓ąŠąĘą╝ąŠąČąĮąŠčüčéąĖ ą┐ąŠ ą▓ą▓ąŠą┤čā ąĖ ą▓čŗą▓ąŠą┤čā I/O, ąĖ ą╝ąŠą┤čāą╗ąĖ ą║ąŠą╝ą╝čāąĮąĖą║ą░čåąĖą╣, ą║ąŠč鹊čĆčŗąĄ DSP ąĖą╝ąĄčÄčé ąŠč湥ąĮčī čĆąĄą┤ą║ąŠ.
ą£ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆčŗ Atmel AVR čģąŠčĆąŠčłąŠ ą┐ąŠą┤čģąŠą┤čÅčé ą┤ą╗čÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ čüąĖą│ąĮą░ą╗ą░, čéą░ą║ ą║ą░ą║ ąĖą╝ąĄčÄčé ą╝ąŠčēąĮčāčÄ ą░čĆčģąĖč鹥ą║čéčāčĆčā, ąĮą░ą▒ąŠčĆ ąĖąĮčüčéčĆčāą║čåąĖą╣ ąĖ ą▓čüčéčĆąŠąĄąĮąĮčŗą╣ ą╝ąĮąŠą│ąŠą║ą░ąĮą░ą╗čīąĮčŗą╣ 10-ą▒ąĖčéąĮčŗą╣ ąÉą”ą¤ (Analog to Digital Converter, ADC). ąĪąĄčĆąĖčÅ megaAVR┬« čéą░ą║ąČąĄ ąĖą╝ąĄąĄčé ą░ą┐ą┐ą░čĆą░čéąĮčŗą╣ čāą╝ąĮąŠąČąĖč鹥ą╗čī, ą║ąŠč鹊čĆčŗą╣ ą▓ą░ąČąĄąĮ ą▓ čüąĖą│ąĮą░ą╗čīąĮąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ.
ąÆ čŹč鹊ą╝ ą┤ąŠą║čāą╝ąĄąĮč鹥 č乊ą║čāčüąĖčĆčāąĄčéčüčÅ čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖąĄ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ čāą╝ąĮąŠąČąĖč鹥ą╗čÅ AVR, ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čĆąĄą│ąĖčüčéčĆąŠą▓ ąŠą▒čēąĄą│ąŠ ąĮą░ąĘąĮą░č湥ąĮąĖčÅ ą┤ą╗čÅ čäčāąĮą║čåąĖąŠąĮą░ą╗čīąĮąŠčüčéąĖ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄčéčüčÅ, ą║ą░ą║ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░čéčī ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ ą┐čĆąĖ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ čü ą░čĆčģąĖč鹥ą║čéčāčĆąŠą╣ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ ą┤čĆąŠą▒ąĮąŠą╣ č鹊čćą║ąĖ, ąĖ ą▓ąŠąĘą╝ąŠąČąĮčŗąĄ ą┐čāčéąĖ ąŠą┐čéąĖą╝ąĖąĘąĖčĆąŠą▓ą░ąĮąĖčÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░. ą¤čĆąĖą╗ąŠąČąĄąĮąŠ ą┤ą▓ą░ ą┐čĆąĖą╝ąĄčĆą░ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ.
ą¤ąŠčüą║ąŠą╗čīą║čā č鹥ąŠčĆąĖčÅ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓ ąĮąĄ čÅą▓ą╗čÅąĄčéčüčÅ čåąĄą╗čīčÄ čŹč鹊ą│ąŠ ą░ą┐ąĮąŠčāčéą░, čĆą░čüą║čĆčŗčé č鹊ą╗čīą║ąŠ ąĮąĄą║ąŠč鹊čĆčŗą╣ ą▒ą░ąĘąĖčü. ąĪą┐ąĖčüąŠą║ čüąŠą▓ąĄčéčāąĄą╝ąŠą╣ ą╗ąĖč鹥čĆą░čéčāčĆčŗ, ą▒ąŠą╗ąĄąĄ ą│ą╗čāą▒ąŠą║ąŠ čĆą░čüą║čĆčŗą▓ą░čÄčēąĄą╣ č鹥ąŠčĆąĖčÄ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓, čāą║ą░ąĘą░ąĮ ą▓ ą║ąŠąĮčåąĄ čŹč鹊ą│ąŠ ą┤ąŠą║čāą╝ąĄąĮčéą░.
[2. ą×čüąĮąŠą▓čŗ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓]
ąÆčüąĄ ą╗ąĖąĮąĄą╣ąĮčŗąĄ čåąĖčäčĆąŠą▓čŗąĄ, ąĖąĮą▓ą░čĆąĖą░ąĮčéąĮčŗąĄ ą┐ąŠ ą▓čĆąĄą╝ąĄąĮąĖ (linear, time-invariant, LTI) čäąĖą╗čīčéčĆčŗ ą╝ąŠą│čāčé ą▒čŗčéčī ąŠą┐ąĖčüą░ąĮčŗ ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮčŗą╝ čāčĆą░ą▓ąĮąĄąĮąĖąĄą╝, ą║ą░ą║ ą┐ąŠą║ą░ąĘą░ąĮąŠ ą▓ ąŻčĆą░ą▓ąĮąĄąĮąĖąĖ 1 (x - ą▓čģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗, y - ą▓čŗčģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗, n - ąĮąŠą╝ąĄčĆ ą▓čŗą▒ąŠčĆą║ąĖ čüąĖą│ąĮą░ą╗ą░, čģą░čĆą░ą║č鹥čĆąĖąĘčāąĄčé ą┐čĆąŠčłąĄą┤čłąĄąĄ ą▓čĆąĄą╝čÅ).
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 1: ąŠčüąĮąŠą▓ąĮąŠąĄ ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠąĄ čāčĆą░ą▓ąĮąĄąĮąĖąĄ ą┤ą╗čÅ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓
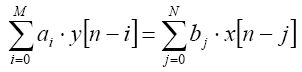
ążąĖą╗čīčéčĆ čāąĮąĖą║ą░ą╗čīąĮąŠ ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ ą┐ąŠ ąĄą│ąŠ ą┐ąŠčĆčÅą┤ą║čā (ąĮą░ąĖą▒ąŠą╗čīčłąĄąĄ ąĖąĘ M ąĖ N) ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ą╝ ai ąĖ bj. ą¤ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ (ąĮą░ąĖą▒ąŠą╗čīčłąĄąĄ ąĖąĘ M ąĖ N) ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčé ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčāčÄ ąĘą░ą┤ąĄčƹȹ║čā ą┐ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ą╝ąĄąČą┤čā ą▓čģąŠą┤ąŠą╝ ąĖ ą▓čŗčģąŠą┤ąŠą╝ čäąĖą╗čīčéčĆą░. ą×ą▒čŗčćąĮąŠ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ (ai, bj) ą╝ą░čüčłčéą░ą▒ąĖčĆčāčÄčéčüčÅ čéą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, čćč鹊 ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé a0 čĆą░ą▓ąĄąĮ 1. ąÆčŗčģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čüąĖą│ąĮą░ą╗ą░ čäąĖą╗čīčéčĆą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ą▓čŗčćąĖčüą╗ąĄąĮąŠ, ą║ą░ą║ ą┐ąŠą║ą░ąĘą░ąĮąŠ ą▓ ąŻčĆą░ą▓ąĮąĄąĮąĖąĖ 2:
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 2: ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠąĄ čāčĆą░ą▓ąĮąĄąĮąĖąĄ ą┤ą╗čÅ ą▓čŗčģąŠą┤ą░ čäąĖą╗čīčéčĆą░

ąĢčüą╗ąĖ x[n] čÅą▓ą╗čÅąĄčéčüčÅ ąĖą╝ą┐čāą╗čīčüąŠą╝ (x==1 ą┐čĆąĖ n==0 ąĖ x==0 ą┐čĆąĖ n!=0), č鹊 ą▓čŗčģąŠą┤ ąĮą░ąĘčŗą▓ą░čÄčé ąĖą╝ą┐čāą╗čīčüąĮčŗą╝ ąŠčéą║ą╗ąĖą║ąŠą╝ čäąĖą╗čīčéčĆą░ h[n].
ążąĖą╗čīčéčĆčŗ ą║ą╗ą░čüčüąĖčäąĖčåąĖčĆčāčÄčéčüčÅ ą┐ąŠ ą┤ą▓čāą╝ čéąĖą┐ą░ą╝, ą▓ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ ąŠčé ąĘąĮą░č湥ąĮąĖčÅ M:
- čéąĖą┐ čäąĖą╗čīčéčĆą░ čü ą║ąŠąĮąĄčćąĮčŗą╝ ąĖą╝ą┐čāą╗čīčüąĮčŗą╝ ąŠčéą║ą╗ąĖą║ąŠą╝, ąÜąśąź-čäąĖą╗čīčéčĆ (Finite Impulse Response, FIR), ą┤ą╗čÅ ąĮąĄą│ąŠ M==0
- čéąĖą┐ čäąĖą╗čīčéčĆą░ čü ą▒ąĄčüą║ąŠąĮąĄčćąĮčŗą╝ ąĖą╝ą┐čāą╗čīčüąĮčŗą╝ ąŠčéą║ą╗ąĖą║ąŠą╝, ąæąśąź-čäąĖą╗čīčéčĆ (Infinite Impulse Response, IIR), ą┤ą╗čÅ ąĮąĄą│ąŠ M!=0
ąĀąĄą░ą╗čīąĮąŠąĄ ąŠčéą╗ąĖčćąĖąĄ čŹčéąĖčģ ą┤ą▓čāčģ čéąĖą┐ąŠą▓ čäąĖą╗čīčéčĆąŠą▓ - ąŠčéčüčāčéčüčéą▓ąĖąĄ (FIR čäąĖą╗čīčéčĆ) ąĖą╗ąĖ ąĮą░ą╗ąĖčćąĖąĄ (IIR čäąĖą╗čīčéčĆ) ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘąĖ čü ą▓čŗčģąŠą┤ą░ ąĮą░ ą▓čģąŠą┤. ążąĖą╗čīčéčĆčŗ IIR ą▓čŗčćąĖčüą╗čÅčÄčéčüčÅ čü čĆąĄą║čāčĆčüąĖąĄą╣, čé. ąĄ. ą┐čĆąĄą┤čŗą┤čāčēąĖąĄ ąĘąĮą░č湥ąĮąĖčÅ (y[n-1]) čāčćą░čüčéą▓čāčÄčé ą▓ ą▓čŗčćąĖčüą╗ąĄąĮąĖąĖ č鹥ą║čāčēąĄą│ąŠ (y[n]) ą▓čŗčģąŠą┤ąĮąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ. ąóąĄčĆą╝ąĖąĮ ą║ąŠąĮąĄčćąĮčŗą╣/ą▒ąĄčüą║ąŠąĮąĄčćąĮčŗą╣ ąŠą┐ąĖčüčŗą▓ą░ąĄčé ą┤ą╗ąĖąĮčā ąŠčéą▓ąĄčéą░ čäąĖą╗čīčéčĆą░ ąĮą░ ą▓čģąŠą┤ąĮąŠą╣ ąĖą╝ą┐čāą╗čīčü (ą┐čĆąĖ ąĖą│ąĮąŠčĆąĖčĆąŠą▓ą░ąĮąĖąĖ čŹčäč乥ą║č鹊ą▓ ą║ą▓ą░ąĮč鹊ą▓ą░ąĮąĖčÅ ą▓ čĆąĄą░ą╗čīąĮąŠą╣ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░). ążąĖą╗čīčéčĆ IIR, čā ą║ąŠč鹊čĆąŠą│ąŠ N==0, ąŠą▒čĆą░ąĘčāąĄčé čüą┐ąĄčåąĖą░ą╗čīąĮčŗą╣ ą║ą╗ą░čüčü čäąĖą╗čīčéčĆą░, ąĮą░ąĘčŗą▓ą░ąĄą╝čŗą╣ "all-pole" čäąĖą╗čīčéčĆ, ąĖą╗ąĖ čäąĖą╗čīčéčĆ, ąĖą╝ąĄčÄčēąĖą╣ č鹊ą╗čīą║ąŠ ą┐ąŠą╗čÄčüčŗ. ąöą╗čÅ ą▒ąŠą╗ąĄąĄ ą┤ąĄčéą░ą╗čīąĮąŠą│ąŠ čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖčÅ čŹčéąĖčģ ą┤ą▓čāčģ ą║ą╗ą░čüčüąŠą▓ čäąĖą╗čīčéčĆąŠą▓ (FIR ąĖ IIR), ąŠą▒čĆą░čēą░ą╣č鹥čüčī ą║ čĆąĄą║ąŠą╝ąĄąĮą┤čāąĄą╝ąŠą╣ ą╗ąĖč鹥čĆą░čéčāčĆąĄ ąĖąĘ čüą┐ąĖčüą║ą░ ą▓ ą║ąŠąĮčåąĄ čüčéą░čéčīąĖ.
ą¦ą░čüč鹊 čåąĖčäčĆąŠą▓čŗąĄ čäąĖą╗čīčéčĆčŗ ąŠą┐ąĖčüčŗą▓ą░čÄčéčüčÅ ą▓ Z-ą┤ąŠą╝ąĄąĮąĄ, ą┤ąŠą╝ąĄąĮąĄ ą║ąŠą╝ą┐ą╗ąĄą║čüąĮąŠą╣ čćą░čüč鹊čéčŗ (ąĮąĄ čüą┐čĆą░čłąĖą▓ą░ą╣č鹥 ą╝ąĄąĮčÅ, čćč鹊 čŹč鹊 čéą░ą║ąŠąĄ). Z-ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ ąŻčĆą░ą▓ąĮąĄąĮąĖčÅ 1 ą┐ąŠą║ą░ąĘą░ąĮąŠ ą▓ ąŻčĆą░ą▓ąĮąĄąĮąĖąĖ 3:
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 3: Z-ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ ąŠčüąĮąŠą▓ąĮąŠą│ąŠ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░
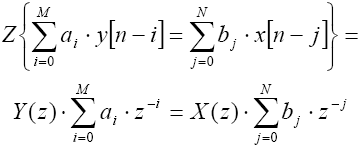
ążčāąĮą║čåąĖčÅ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ H(z) ąŠą▒čŗčćąĮąŠ ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗čÅąĄčéčüčÅ ą┤ą╗čÅ čäąĖą╗čīčéčĆą░, ą┐ąŠčüą║ąŠą╗čīą║čā čŹč鹊 ą┤ą░ąĄčé ą║ąŠą╝ą┐ą░ą║čéąĮąŠąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖąĄ, ąĖ ą┐ąŠąĘą▓ąŠą╗čÅąĄčé ą╗ąĄą│ą║ąŠ ą▓čŗą┐ąŠą╗ąĮąĖčéčī čćą░čüč鹊čéąĮčŗą╣ ą░ąĮą░ą╗ąĖąĘ. ążčāąĮą║čåąĖčÅ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ąĘą░ą┤ą░ąĄčéčüčÅ ą║ą░ą║ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ą╝ąĄąČą┤čā ą▓čŗčģąŠą┤ąŠą╝ ąĖ ą▓čģąŠą┤ąŠą╝ čäąĖą╗čīčéčĆą░ ą▓ Z-ą┤ąŠą╝ąĄąĮąĄ, ą║ą░ą║ ą┐ąŠą║ą░ąĘą░ąĮąŠ ą▓ ąŻčĆą░ą▓ąĮąĄąĮąĖąĖ 4. ą×ą▒čĆą░čéąĖč鹥 ą▓ąĮąĖą╝ą░ąĮąĖąĄ, čćč鹊 čäčāąĮą║čåąĖčÅ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ čÅą▓ą╗čÅąĄčéčüčÅ Z-ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄą╝ ąĖą╝ą┐čāą╗čīčüąĮąŠą│ąŠ ąŠčéą▓ąĄčéą░ čäąĖą╗čīčéčĆą░ h[n].
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 4: čäčāąĮą║čåąĖčÅ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ą┤ą╗čÅ ąŠčüąĮąŠą▓ąĮąŠą│ąŠ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░
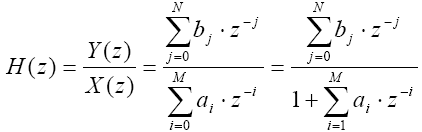
ąÜą░ą║ ą╝ąŠąČąĮąŠ čāą▓ąĖą┤ąĄčéčī, čćąĖčüą╗ąĖč鹥ą╗čī ąŠą┐ąĖčüčŗą▓ą░ąĄčé čćą░čüčéčī feed-forward (ą▒ąĄąĘ ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘąĖ), ą░ ąĘąĮą░ą╝ąĄąĮą░č鹥ą╗čī - čćą░čüčéčī feedback (čü ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘčīčÄ). ąöą╗čÅ ą▒ąŠą╗ąĄąĄ ą┤ąĄčéą░ą╗čīąĮąŠą│ąŠ čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖčÅ Z-ą┤ąŠą╝ąĄąĮą░, ąŠą▒čĆą░čēą░ą╣č鹥čüčī ą║ čĆąĄą║ąŠą╝ąĄąĮą┤čāąĄą╝ąŠą╣ ą╗ąĖč鹥čĆą░čéčāčĆąĄ ąĖąĘ čüą┐ąĖčüą║ą░ ą▓ ą║ąŠąĮčåąĄ čüčéą░čéčīąĖ.
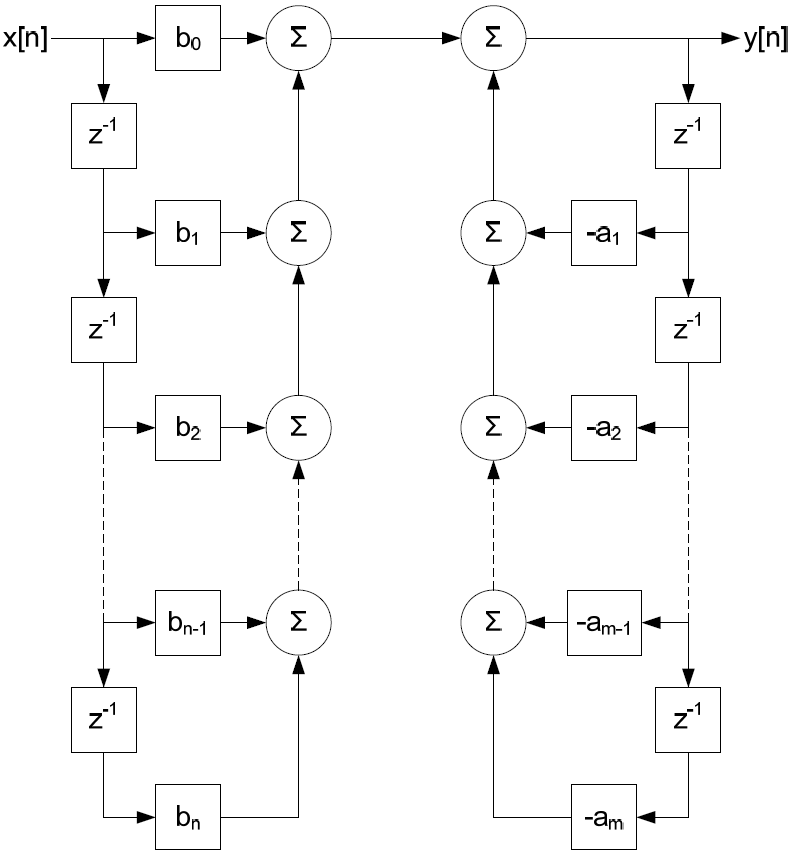
ąöą╗čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░ ą┐ąŠ ąĘą░ą┤ą░ąĮąĮąŠą╣ čäčāąĮą║čåąĖąĖ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ą▓ą░ąČąĮąŠ ąĘąĮą░čéčī, čćč鹊 z ą▓ Z-ą┤ąŠą╝ąĄąĮąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé 菹╗ąĄą╝ąĄąĮčé ąĘą░ą┤ąĄčƹȹ║ąĖ, ąĖ 菹║čüą┐ąŠąĮąĄąĮčéą░ ąĘą░ą┤ą░ąĄčé ą┤ą╗ąĖąĮčā ąĘą░ą┤ąĄčƹȹ║ąĖ ą▓ ąĄą┤ąĖąĮąĖčåą░čģ ą▓čŗą▒ąŠčĆąŠą║ (ą▓ ą┐čĆąŠą╝ąĄąČčāčéą║ą░čģ ą▓čĆąĄą╝ąĄąĮąĖ ą╝ąĄąČą┤čā ą▓čŗą▒ąŠčĆą║ą░ą╝ąĖ). ąĀąĖčüčāąĮąŠą║ 2-1 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čüčģąĄą╝čā čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░ ą▓ ą¤čĆčÅą╝ąŠą╣ ążąŠčĆą╝ąĄ 1.
ąĀąĖčüčāąĮąŠą║ 2-1: ą¤čĆčÅą╝ą░čÅ ążąŠčĆą╝ą░ 1 ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ ąŠčüąĮąŠą▓ąĮąŠą│ąŠ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░.
[3. ąĪąŠąŠą▒čĆą░ąČąĄąĮąĖčÅ, ą┐čĆąĖąĮąĖą╝ą░ąĄą╝čŗąĄ ą▓ąŠ ą▓ąĮąĖą╝ą░ąĮąĖąĄ ą┐čĆąĖ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░]
ąÜąŠą│ą┤ą░ ą┐čĆąŠąĄą║čéąĖčĆčāčÄčé čäąĖą╗čīčéčĆ ąĮą░ ą▓čŗą▒čĆą░ąĮąĮąŠą╣ ą░čĆčģąĖč鹥ą║čéčāčĆąĄ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ (MCU), ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ą┐čĆąĖąĮčÅčéčī ą▓ąŠ ą▓ąĮąĖą╝ą░ąĮąĖąĄ ąĮąĄčüą║ąŠą╗čīą║ąŠ ą╝ąŠą╝ąĄąĮč鹊ą▓. ąØą░ą┐čĆąĖą╝ąĄčĆ:
- č鹊čćąĮąŠčüčéčī (ą║ąŠą╗ąĖč湥čüčéą▓ąŠ ą▒ąĖčé) ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ čüąĖą│ąĮą░ą╗ą░ ąĮą░ ą▓čģąŠą┤ąĄ ąĖ ą▓čŗčģąŠą┤ąĄ ą▒čāą┤ąĄčé ą▓ą╗ąĖčÅčéčī ąĮą░ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą┤ąŠą┐čāčüčéąĖą╝ąŠąĄ čāčüąĖą╗ąĄąĮąĖąĄ čäąĖą╗čīčéčĆą░ ąĖ ąĄą│ąŠ ą┐čĆąŠą┐čāčüą║ąĮčāčÄ čüą┐ąŠčüąŠą▒ąĮąŠčüčéčī (throughput).
- č鹊čćąĮąŠčüčéčī ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ ą▓ą╗ąĖčÅąĄčé ąĮą░ ąŠčéą▓ąĄčé ą┐ąŠ čćą░čüč鹊č鹥, ąÉą¦ąź (frequency response) ąĖ ą┐čĆąŠą┐čāčüą║ąĮčāčÄ čüą┐ąŠčüąŠą▒ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░.
- ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ ą▓ą╗ąĖčÅąĄčé ąĮą░ ą┐čĆąŠą┐čāčüą║ąĮčāčÄ čüą┐ąŠčüąŠą▒ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░.
- ą┤čĆąŠą▒ąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ čéčĆąĄą▒čāčÄčé ąĮąĄą║ąŠč鹊čĆčŗčģ čāčģąĖčēčĆąĄąĮąĖą╣ ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ (ą▓ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░čģ AVR ąŠąĮ ąĖą╝ąĄąĮąĮąŠ čéą░ą║ąŠą╣).
ąŁčéąĖ ąĖ ą┤čĆčāą│ąĖąĄ ą▓ąŠą┐čĆąŠčüčŗ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ąŠą▒čüčāąČą┤ą░čÄčéčüčÅ ą▓ čŹč鹊ą╣ čüąĄą║čåąĖąĖ čüčéą░čéčīąĖ. ąÆ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖąĄ ą┐čĆąĖą▓ąĄą┤ąĄąĮąŠ ą▒čŗčüčéčĆąŠąĄ ąŠą┐ąĖčüą░ąĮąĖąĄ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ AVR ąĖ ą▓ąĖčĆčéčāą░ą╗čīąĮąŠą│ąŠ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, ą┐ąŠč鹊ą╝čā čćč鹊 ąĘąĮą░ąĮąĖčÅ ąŠ ąĮąĖčģ ą▓ą░ąČąĮčŗ ą┤ą╗čÅ ą┐ąŠąĮąĖą╝ą░ąĮąĖčÅ čĆą░ą▒ąŠčéčŗ ą║ąŠą┤ą░ čäąĖą╗čīčéčĆą░.
3.1 ąÉą┐ą┐ą░čĆą░čéąĮčŗą╣ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī, ą▓čüčéčĆąŠąĄąĮąĮčŗą╣ ą▓ AVR
ą¤ąŠčüą║ąŠą╗čīą║čā AVR ąĖą╝ąĄąĄčé 8-ą▒ąĖčéąĮčāčÄ ą░čĆčģąĖč鹥ą║čéčāčĆčā, ą░ą┐ą┐ą░čĆą░čéąĮčŗą╣ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī 8-ą▒ąĖčéąĮčŗą╣, ą░ ą┐čĆąĖ ą┐ąĄčĆąĄą╝ąĮąŠąČąĄąĮąĖąĖ ą┤ą▓čāčģ čćąĖčüąĄą╗ 8 ą▒ąĖčé ąĮą░ 8 ą▒ąĖčé ą┐ąŠą╗čāčćą░ąĄčéčüčÅ čĆąĄąĘčāą╗čīčéą░čé 16 ą▒ąĖčé. ą¤ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ (ą░ą┐ąĮąŠčāčé AVR223) čĆą░ą▒ąŠčéą░ąĄčé ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čéčĆąĄčģ čĆą░ąĘą╗ąĖčćąĮčŗčģ ąĖąĮčüčéčĆčāą║čåąĖą╣ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░: MUL (ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ą░čÅ ąĖąĮčüčéčĆčāą║čåąĖčÅ čāą╝ąĮąŠąČąĄąĮąĖčÅ), MULS (čāą╝ąĮąŠąČąĄąĮąĖąĄ čüąŠ ąĘąĮą░ą║ąŠą╝) ąĖ MULSU (ą┐ąĄčĆąĄą╝ąĮąŠąČąĄąĮąĖąĄ čćąĖčüą╗ą░ čüąŠ ąĘąĮą░ą║ąŠą╝ ąĮą░ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ąŠąĄ).
ąÉą╗ą│ąŠčĆąĖčéą╝ čäąĖą╗čīčéčĆą░ čüąŠčüč鹊ąĖčé ąĖąĘ čüčāą╝ą╝čŗ čĆąĄąĘčāą╗čīčéą░č鹊ą▓ ąĮąĄčüą║ąŠą╗čīą║ąĖčģ čłą░ą│ąŠą▓ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣. ą¤ąĄčĆą▓čŗą╣ čĆąĄąĘčāą╗čīčéą░čé ą▓čŗčćąĖčüą╗čÅąĄčéčüčÅ "ą┐čĆąŠčüčéčŗą╝" (MUL) ą┐ąĄčĆąĄą╝ąĮąŠąČąĄąĮąĖąĄą╝ ą╝ąĄąČą┤čā ą┤ą▓čāą╝čÅ N-ą▒ąĖčéąĮčŗą╝ąĖ čćąĖčüą╗ą░ą╝ąĖ, ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 č湥ą│ąŠ ą┐ąŠą╗čāčćą░ąĄčéčüčÅ 2N-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé. ą¤ąĄčĆąĄą╝ąĮąŠąČąĄąĮąĖąĄ ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ čü ąŠą┤ąĮąĖą╝ ą▒ą░ą╣č鹊ą╝, ą║ąŠč鹊čĆčŗą╣ čāą╝ąĮąŠąČą░ąĄčéčüčÅ ąĮą░ ą║ą░ąČą┤čŗą╣ ąĖąĘ ą╝ąĮąŠąČąĖč鹥ą╗ąĄą╣, ąĖ čĆąĄąĘčāą╗čīčéą░čé čüąŠčģčĆą░ąĮčÅąĄčéčüčÅ 2N-ą▒ąĖčéąĮąŠą╝ "ą░ą║ą║čāą╝čāą╗čÅč鹊čĆąĄ". ąĪą╗ąĄą┤čāčÄčēąĖą╣ čĆąĄąĘčāą╗čīčéą░čé ą▓čŗčćąĖčüą╗čÅąĄčéčüčÅ ąĖ ą┤ąŠą▒ą░ą▓ą╗čÅąĄčéčüčÅ ą▓ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ, č湥ą╝ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖčéčüčÅ čéą░ą║ ąĮą░ąĘčŗą▓ą░ąĄą╝ą░čÅ ąŠą┐ąĄčĆą░čåąĖčÅ multiply-and-accumulate (MAC).
ą¤čĆąĖą╝ąĄčĆčŗ čäąĖą╗čīčéčĆąŠą▓ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ ąĖčüą┐ąŠą╗čīąĘčāčÄčé ą┤ą▓ąĄ čĆą░ąĘą╗ąĖčćąĮčŗąĄ ąŠą┐ąĄčĆą░čåąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ:
muls16x16_24
mac16x16_24
ąŚą┤ąĄčüčī ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ čāą╝ąĮąŠąČąĄąĮąĖąĄ čüąŠ ąĘąĮą░ą║ąŠą╝ ą┤ą▓čāčģ 16-ą▒ąĖčéąĮčŗčģ ąŠą┐ąĄčĆą░ąĮą┤ąŠą▓ čü 24-ą▒ąĖčéąĮčŗą╝ čĆąĄąĘčāą╗čīčéą░č鹊ą╝. ąĀąĄąĘčāą╗čīčéą░čé ąĮąĄ 32-ą▒ąĖčéąĮčŗą╣, ą┐ąŠčüą║ąŠą╗čīą║čā ą▓čģąŠą┤ąĮčŗąĄ ą▓čŗą▒ąŠčĆą║ąĖ ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ ą┐ąŠą┤ąŠą▒čĆą░ąĮčŗ čéą░ą║, čćč鹊 ąĮąĄ ąĖčüą┐ąŠą╗čīąĘčāčÄčé ą▓ąĄčüčī ą┤ąĖą░ą┐ą░ąĘąŠąĮ 16 ą▒ąĖčé.
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 AVR čéą░ą║ąČąĄ ąĖą╝ąĄąĄčé ąĖąĮčüčéčĆčāą║čåąĖąĖ ą┤ą╗čÅ ą┤čĆąŠą▒ąĮčŗčģ ą┐ąĄčĆąĄą╝ąĮąŠąČąĄąĮąĖą╣, ąĮąŠ ąŠąĮąĖ ąĮąĄ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ. ąŚą░ ą┐ąŠą┤čĆąŠą▒ąĮąŠčüčéčÅą╝ąĖ ąŠą▒čĆą░čēą░ą╣č鹥čüčī ą║ ą░ą┐ąĮąŠčāčéčā ŌĆ£AVR201: Using the AVR Hardware MultiplierŌĆØ (AVR201: ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ AVR).
3.2 ąÆąĖčĆčéčāą░ą╗čīąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ AVR
ąŻ AVR ąĮąĄčé ą▓čŗą┤ąĄą╗ąĄąĮąĮąŠą│ąŠ čüą┐ąĄčåąĖą░ą╗čīąĮąŠą│ąŠ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, ą▓ą╝ąĄčüč鹊 ąĮąĄą│ąŠ AVR ą┐ąŠąĘą▓ąŠą╗čÅąĄčé ą╗čÄą▒čŗą╝ ąĖąĘ 32-čģ ą▓ąŠčüčīą╝ąĖą▒ąĖčéąĮčŗčģ čĆąĄą│ąĖčüčéčĆąŠą▓ ąŠą▒čēąĄą│ąŠ ąĮą░ąĘąĮą░č湥ąĮąĖčÅ (GPIO registers) čĆą░ą▒ąŠčéą░čéčī ą▓ č乊čĆą╝ąĄ "ą▓ąĖčĆčéčāą░ą╗čīąĮąŠą│ąŠ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░". ąÆ čŹč鹊ą╣ čüčéą░čéčīąĄ ą▓ąĖčĆčéčāą░ą╗čīąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ ą▒čāą┤ąĄčé ą┐čĆąŠčüč鹊 ąĮą░ąĘčŗą▓ą░ąĄčéčüčÅ "ą░ą║ą║čāą╝čāą╗čÅč鹊čĆąŠą╝". ąóą░ą║ąŠą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ ą▒ąŠą╗ąĄąĄ ą│ąĖą▒ą║ąĖą╣, č湥ą╝ ąŠą▒čŗčćąĮčŗąĄ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆčŗ, ąĖčüą┐ąŠą╗čīąĘčāąĄą╝čŗąĄ ą▓ ą┤čĆčāą│ąĖčģ ą░čĆčģąĖč鹥ą║čéčāčĆą░čģ (čģąŠčéčÅ, ą▓ąŠąĘą╝ąŠąČąĮąŠ ąĖąĮąŠą│ą┤ą░ čĆą░ą▒ąŠčéą░ąĄčé ą╝ąĄą┤ą╗ąĄąĮąĮąĄąĄ).
ąØą░ą┐čĆąĖą╝ąĄčĆ, ąĄčüą╗ąĖ ą┤ą╗čÅ AVR ąĮąĄąŠą▒čģąŠą┤ąĖą╝ 24-ą▒ąĖčéąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ, čćč鹊ą▒čŗ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖčéčī (MUL) ą┤ą▓ąĄ 12-ą▒ąĖčéąĮčŗąĄ ą▓ąĄą╗ąĖčćąĖąĮčŗ, ą║ąŠą╝ą▒ąĖąĮąĖčĆčāčÄčéčüčÅ čéčĆąĖ 8-ą▒ąĖčéąĮčŗčģ GP-čĆąĄą│ąĖčüčéčĆą░ ą▓ ąŠą┤ąĖąĮ 24-ą▒ąĖčéąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ. ąĢčüą╗ąĖ MAC čéčĆąĄą▒čāąĄčé 40-ą▒ąĖčéąĮąŠą│ąŠ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, ą║ąŠą╝ą▒ąĖąĮąĖčĆčāčÄčéčüčÅ ą┐čÅčéčī 8-ą▒ąĖčéąĮčŗčģ čĆąĄą│ąĖčüčéčĆąŠą▓. ąóą░ą║ą░čÅ ą│ąĖą▒ą║ąŠčüčéčī ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░ ąĮąĄ čéčĆąĄą▒čāąĄčé čĆą░ąĘą┤ąĄą╗ąĄąĮąĖčÅ ąŠą┐ąĄčĆą░čåąĖą╣ ąĮą░ čĆąĄąĘčāą╗čīčéą░čéčŗ ąĖ ą┐ąŠą┤čĆąĄąĘčāą╗čīčéą░čéčŗ, ą┐ąĄčĆąĄąĮąŠčüąĖą╝čŗčģ čéčāą┤ą░ ąĖ ąŠą▒čĆą░čéąĮąŠ ą▓ąŠ ą▓čĆąĄą╝čÅ ąŠą┐ąĄčĆą░čåąĖą╣ MAC (ą║ąŠč鹊čĆčŗąĄ čéčĆąĄą▒čāčÄčéčüčÅ, ąĄčüą╗ąĖ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ ąĖą╝ąĄąĄčé čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮčāčÄ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī 32 ąĖą╗ąĖ ą╝ąĄąĮąĄąĄ ą▒ąĖčé).
ąōąĖą▒ą║ąŠčüčéčī ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░ AVR - ą▓ą░ąČąĮčŗą╣ ąĖąĮčüčéčĆčāą╝ąĄąĮčé ą┤ą╗čÅ ąŠą▒čģąŠą┤ą░ ą┐čĆąŠą▒ą╗ąĄą╝ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ą▓ ą░ą╗ą│ąŠčĆąĖčéą╝ą░čģ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ (Fixed Point, FP), ą║ąŠč鹊čĆčŗąĄ ą▒čāą┤čāčé ąŠą▒čüčāąČą┤ąĄąĮčŗ ą┤ą░ą╗ąĄąĄ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ.
3.3 ą¤ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖąĄ ąĘąĮą░č湥ąĮąĖą╣ ą▓ ąŠą┐ąĄčĆą░čåąĖčÅčģ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣.
ą¤ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖąĄ ą╝ąŠąČąĄčé ą┐čĆąŠąĖąĘąŠą╣čéąĖ ą▓ ą┤ą▓čāčģ ą╝ąĄčüčéą░čģ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░ - ą▓ ą┐čĆąŠą╝ąĄąČčāč鹊čćąĮčŗčģ čĆąĄąĘčāą╗čīčéą░čéą░čģ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ ąĖ ąĮą░ ą▓čŗčģąŠą┤ąĄ čäąĖą╗čīčéčĆą░. ą¤ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖąĄ ą▓ ą┐čĆąŠą╝ąĄąČčāč鹊čćąĮčŗčģ čĆąĄąĘčāą╗čīčéą░čéą░čģ ą╝ąŠąČąĄčé ą┐čĆąŠąĖąĘąŠą╣čéąĖ:
- ą┐čĆąĖ ą┐ąĄčĆąĄą╝ąĮąŠąČąĄąĮąĖąĖ ą▓ąĄą╗ąĖčćąĖąĮ čü čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčīčÄ N1 ąĖ N2, ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 ą┐ąŠą╗čāčćąĖčéčüčÅ čĆąĄąĘčāą╗čīčéą░čé ąĖąĘ N1+N2 ą▒ąĖčé.
- čüą╗ąŠąČąĄąĮąĖąĄ ą┤ą▓čāčģ ą▓ąĄą╗ąĖčćąĖąĮ ą╝ąŠąČąĄčé ą▓čŗą┤ą░čéčī čüčāą╝ą╝čā, ą║ąŠč鹊čĆą░čÅ ąĖą╝ąĄąĄčé ąĮą░ 1 ą▒ąĖčé ą▒ąŠą╗čīčłąĄ čĆą░ąĘą╝ąĄčĆ, č湥ą╝ čüą░ą╝čŗą╣ ą▒ąŠą╗čīčłąŠą╣ ą┐ąŠ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ ąŠą┐ąĄčĆą░ąĮą┤ čüą╗ąŠąČąĄąĮąĖčÅ. ąØą░ą┐čĆąĖą╝ąĄčĆ, čĆą░čüčüą╝ąŠčéčĆąĖą╝ ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 5 ą┤ą╗čÅ FIR čäąĖą╗čīčéčĆą░ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░:
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 5: ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠąĄ čāčĆą░ą▓ąĮąĄąĮąĖąĄ ą┤ą╗čÅ čäąĖą╗čīčéčĆą░ FIR 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
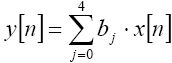
ąÆčŗčģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čäąĖą╗čīčéčĆą░ y[n] čĆą░ą▓ąĮąŠ čüčāą╝ą╝ąĄ ą┐čÅčéąĖ ą┐čĆąŠą╝ąĄąČčāč鹊čćąĮčŗčģ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ. ąĢčüą╗ąĖ ą┐čĆąĄą┤ą┐ąŠą╗ąŠąČąĖčéčī, čćč鹊 ą▓čģąŠą┤ąĮčŗąĄ ą▓čŗą▒ąŠčĆą║ąĖ x[n] ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ bj ąĖą╝ąĄčÄčé ą▓ąĄą╗ąĖčćąĖąĮčŗ 16 ą▒ąĖčé čüąŠ ąĘąĮą░ą║ąŠą╝, ą░ą╗ą│ąŠčĆąĖčéą╝ ą┐ąŠčéčĆąĄą▒čāąĄčé 34-ą▒ąĖčéąĮąŠą│ąŠ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░ - čüą╝. čĆą░čüč湥čé ą▓ ąŻčĆą░ą▓ąĮąĄąĮąĖąĖ 6. ąÆ čŹč鹊ą╝ čāčĆą░ą▓ąĮąĄąĮąĖąĖ N - čéčĆąĄą▒čāąĄą╝ą░čÅ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, K - čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī ąŠą┐ąĄčĆą░ąĮą┤ąŠą▓ (x[n] ąĖ bj) ąĮąĄ čüčćąĖčéą░čÅ ą▒ąĖčéą░ ąĘąĮą░ą║ą░, M - ą║ąŠą╗ąĖč湥čüčéą▓ąŠ čüą╗ą░ą│ą░ąĄą╝čŗčģ (ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ +1). ą×ą┤ąĖąĮ ą┤ąŠą▒ą░ą▓ą╗čÅąĄą╝čŗą╣ ą▒ąĖčé - čŹč鹊 ą▒ąĖčé ąĘąĮą░ą║ą░.
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 6: čéčĆąĄą▒čāąĄą╝ą░čÅ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░ ą┤ą╗čÅ čäąĖą╗čīčéčĆą░ FIR 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
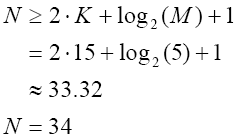
ąÉą║ą║čāą╝čāą╗čÅč鹊čĆ ą┤ą╗čÅ ą┤ą░ąĮąĮąŠą│ąŠ čüą╗čāčćą░čÅ ą┤ąŠą╗ąČąĄąĮ čüąŠčüč鹊čÅčéčī ąĖąĘ 5 ą▒ą░ą╣čé čĆąĄą│ąĖčüčéčĆąŠą▓ GPIO (40 ą▒ąĖčé), čćč鹊ą▒čŗ čüąŠčģčĆą░ąĮąĖčéčī ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčāčÄ ą▓ąĄą╗ąĖčćąĖąĮčā, ą║ąŠč鹊čĆą░čÅ ą╝ąŠąČąĄčé ą▓čüčéčĆąĄčéąĖčéčīčüčÅ ą▓ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅčģ.
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ą┤ą╗čÅ čäąĖą╗čīčéčĆą░ IIR ą▓čŗčģąŠą┤ąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ čäąĖą╗čīčéčĆą░ čāčćą░čüčéą▓čāčÄčé ą▓ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅčģ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░. ąĢčüą╗ąĖ ą▓čŗčģąŠą┤ąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ čäąĖą╗čīčéčĆą░ ąĖą╝ąĄčÄčé ą▒ą×ą╗čīčłčāčÄ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī, č湥ą╝ ą▓čģąŠą┤ąĮčŗąĄ, čĆą░ąĘą╝ąĄčĆ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą┐ąŠą┤ąŠą▒čĆą░ąĮ čü čāč湥č鹊ą╝ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ ą▓čŗčģąŠą┤ą░ čäąĖą╗čīčéčĆą░.
ą¦č鹊ą▒čŗ ąĖąĘą▒ąĄąČą░čéčī ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ąĮą░ čüčéą░ą┤ąĖąĖ ą▓čŗčģąŠą┤ą░ čäąĖą╗čīčéčĆą░, čāčüąĖą╗ąĄąĮąĖąĄ čäąĖą╗čīčéčĆą░ ą┤ąŠą╗ąČąĮąŠ ą▒čŗčéčī ąŠą│čĆą░ąĮąĖč湥ąĮąŠ, čćč鹊ą▒čŗ čüčéą░ą╗ąŠ ą▓ąŠąĘą╝ąŠąČąĮčŗą╝ ą┐čĆąĄą┤čüčéą░ą▓ąĖčéčī čĆąĄąĘčāą╗čīčéą░čé čü ąĘą░ą┤ą░ąĮąĮąŠą╣ č鹊čćąĮąŠčüčéčīčÄ (čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčīčÄ) ą┤ą╗čÅ ą▓čŗčģąŠą┤ą░. ą×ą│čĆą░ąĮąĖč湥ąĮąĖąĄ čāčüąĖą╗ąĄąĮąĖčÅ ą▒čāą┤ąĄčé, ą║ąŠąĮąĄčćąĮąŠ, ąĘą░ą▓ąĖčüąĄčéčī ąŠčé čüą┐ąĄą║čéčĆą░ ąĖ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ (ą┐ąŠ ąŠčéąĮąŠčłąĄąĮąĖčÄ ą║ ą▓čŗčģąŠą┤čā) ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░.
ąĪą░ą╝čŗą╣ ą║ąŠąĮčüąĄčĆą▓ą░čéąĖą▓ąĮčŗą╣ ą║čĆąĖč鹥čĆąĖą╣ ą┤ą╗čÅ č鹊ą│ąŠ, čćč鹊ą▒čŗ ąĖąĘą▒ąĄąČą░čéčī ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ą▓ čüąŠčüč鹊čÅąĮąĖčÅčģ ą▓čŗčģąŠą┤ą░, čüąŠčüč鹊ąĖčé ą▓ č鹊ą╝, čćč鹊ą▒čŗ ą░ą▒čüąŠą╗čÄčéąĮą░čÅ čüčāą╝ą╝ą░ ąĖą╝ą┐čāą╗čīčüąĮčŗčģ ąŠčéą▓ąĄč鹊ą▓ čäąĖą╗čīčéčĆą░, ą┐ąŠą╝ąĮąŠąČąĄąĮąĮą░čÅ ąĮą░ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĮą░ ą▓čģąŠą┤ąĄ ąĮąĄ ą┐čĆąĄą▓čŗčłą░ą╗ą░ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ą▓čŗčģąŠą┤ą░, čüą╝. ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 7.
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 7: ą║ąŠąĮčüąĄčĆą▓ą░čéąĖą▓ąĮčŗą╣ ą║čĆąĖč鹥čĆąĖą╣ ąŠčéčüčāčéčüčéą▓ąĖčÅ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ąĮą░ ą▓čŗčģąŠą┤ąĄ čäąĖą╗čīčéčĆą░.
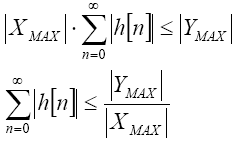
ąĢčüą╗ąĖ ąĖą╝ą┐čāą╗čīčüąĮčŗą╣ ąŠčéą▓ąĄčé ąĮąĄ čāą┤ąŠą▓ą╗ąĄčéą▓ąŠčĆčÅąĄčé čŹč鹊ą╝čā ą║čĆąĖč鹥čĆąĖčÄ, ąŠąĮ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą┐čĆąŠčüč鹊 čāą╝ąĮąŠąČąĄąĮ ąĮą░ čäą░ą║č鹊čĆ, ą║ąŠč鹊čĆčŗą╣ čāą╝ąĄąĮčīčłąĖčé ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čüčāą╝ą╝čŗ.
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ą┤ą╗čÅ čåąĄą╗čŗčģ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ ąĮą░ 1 ą╝ąĄąĮčīčłąĄ, č湥ą╝ ą░ą▒čüąŠą╗čÄčéąĮčŗą╣ ą╝ąĖąĮąĖą╝čāą╝ ąŠčéčĆąĖčåą░č鹥ą╗čīąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ. ą¤čĆąĄą┤ą┐ąŠą╗ąŠąČąĖą╝, čćč鹊 ą▓čģąŠą┤ ąĖą╝ąĄąĄčé čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī M ą▒ąĖčé ąĖ ą▓čŗčģąŠą┤ ąĖą╝ąĄąĄčé čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī N ą▒ąĖčé, ą▓ čŹč鹊ą╝ čüą╗čāčćą░ąĄ ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 8 ą┐ąŠą║ą░ąČąĄčé ą║čĆąĖč鹥čĆąĖą╣ ą┤ą╗čÅ ąĮą░ąĖčģčāą┤čłąĄą│ąŠ čüčåąĄąĮą░čĆąĖčÅ.
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 8: "ąĮą░ąĖčģčāą┤čłąĖą╣ čüą╗čāčćą░ą╣" ą║ąŠąĮčüąĄčĆą▓ą░čéąĖą▓ąĮąŠą│ąŠ ą║čĆąĖč鹥čĆąĖčÅ ą┤ą╗čÅ čåąĄą╗čŗčģ čüąŠ ąĘąĮą░ą║ąŠą╝.
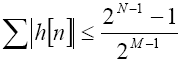
ąźąŠčéčÅ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ čŹč鹊ą│ąŠ ą║čĆąĖč鹥čĆąĖčÅ ą│ą░čĆą░ąĮčéąĖčĆčāąĄčé ąŠčéčüčāčéčüčéą▓ąĖąĄ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ, ąĄą│ąŠ ąĮąĄą┤ąŠčüčéą░č鹊ą║ - čüčāčēąĄčüčéą▓ąĄąĮąĮąŠąĄ čüąĮąĖąČąĄąĮąĖąĄ čāčüąĖą╗ąĄąĮąĖčÅ čäąĖą╗čīčéčĆą░. ąźą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ ą╝ąŠą│čāčé ą▒čŗčéčī čéą░ą║ąĖą╝ąĖ, čćč鹊 čŹč鹊čé ą║čĆąĖč鹥čĆąĖą╣ ą▒čāą┤ąĄčé čüą╗ąĖčłą║ąŠą╝ ą┐ąĄčüčüąĖą╝ąĖčüčéąĖč湥ąĮ.
ąöčĆčāą│ąŠą╣ ąŠą▒čēąĖą╣ ą║čĆąĖč鹥čĆąĖą╣, ą║ąŠč鹊čĆčŗą╣ ą╗čāčćčłąĄ ą┐ąŠą┤čģąŠą┤ąĖčé ą┤ą╗čÅ čāąĘą║ąŠą┐ąŠą╗ąŠčüąĮčŗčģ čüąĖą│ąĮą░ą╗ąŠą▓ (čéą░ą║ąĖčģ, ą║ą░ą║ čüąĖąĮčāčüąŠąĖą┤ą░ą╗čīąĮčŗą╣ čüąĖą│ąĮą░ą╗), čüąŠčüč鹊ąĖčé ą▓ č鹊ą╝, čćč鹊 ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ čāčüąĖą╗ąĄąĮąĖąĄ čäąĖą╗čīčéčĆą░, čāą╝ąĮąŠąČąĄąĮąĮąŠąĄ ąĮą░ ą░ą▒čüąŠą╗čÄčéąĮąŠąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░, ąĮąĄ ą╝ąŠąČąĄčé ą┐čĆąĄą▓čŗčüąĖčéčī ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ą▓čŗčģąŠą┤ą░. ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 9 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čŹč鹊čé ą║čĆąĖč鹥čĆąĖą╣.
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 9: ą║čĆąĖč鹥čĆąĖą╣ ą┤ą╗čÅ čāčüčéčĆą░ąĮąĄąĮąĖčÅ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ą┐čĆąĖ čāąĘą║ąŠą┐ąŠą╗ąŠčüąĮčŗčģ čüąĖą│ąĮą░ą╗ą░čģ.

ąśą╝ąĄąĮąĮąŠ čŹč鹊čé ą║čĆąĖč鹥čĆąĖą╣ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┤ą╗čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ: čü ąŠą┤ąĖąĮą░ą║ąŠą▓ąŠą╣ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčīčÄ ą┤ą╗čÅ ą▓čģąŠą┤ą░ ąĖ ą▓čŗčģąŠą┤ą░ čāčüąĖą╗ąĄąĮąĖąĄ čā čäąĖą╗čīčéčĆą░ ąĮąĄ ą┤ąŠą╗ąČąĮąŠ ą┐čĆąĄą▓čŗčłą░čéčī 0 dB (ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé ą┐ąĄčĆąĄą┤ą░čćąĖ ąĮąĄ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą▒ąŠą╗čīčłąĄ 1).
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ąŠą│čĆą░ąĮąĖč湥ąĮąĖąĄ čāčüąĖą╗ąĄąĮąĖčÅ ąĘą░ą▓ąĖčüąĖčé ąŠčé čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░, ą┐ąŠčŹč鹊ą╝čā čü ą┐ąŠą╝ąŠčēčīčÄ ąĮąĄą║ąŠč鹊čĆąŠą│ąŠ 菹║čüą┐ąĄčĆąĖą╝ąĄąĮčéąĖčĆąŠą▓ą░ąĮąĖčÅ ą╝ąŠąČąĮąŠ ąĮą░ą╣čéąĖ ąŠą┐čéąĖą╝ą░ą╗čīąĮčŗą╣ ą╗ąĖą╝ąĖčé.
3.4 ą£ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓.
ąöčĆčāą│ąŠą╣ ą▓ą░ąČąĮčŗą╣ ą▓ąŠą┐čĆąŠčü - ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ ąĮą░ ą░čĆčģąĖč鹥ą║čéčāčĆąĄ, ąĖčüą┐ąŠą╗čīąĘčāčÄčēąĄą╣ čćąĖčüą╗ą░ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣ (Fixed Point, FP). FP ą▓ąŠą▓čüąĄ ąĮąĄ ąŠąĘąĮą░čćą░ąĄčé č鹊čé čäą░ą║čé, čćč鹊 ą▓čüąĄ čćąĖčüą╗ą░ ąŠą▒čÅąĘą░č鹥ą╗čīąĮąŠ ą┤ąŠą╗ąČąĮčŗ ą▒čŗčéčī čåąĄą╗čŗą╝ąĖ - ą║ą░ą║ čāąČąĄ ą▒čŗą╗ąŠ čāą║ą░ąĘą░ąĮąŠ, ą┤ąŠčüčéčāą┐ąĮąŠ čéą░ą║ąČąĄ ą┤čĆąŠą▒ąĮąŠąĄ FP čāą╝ąĮąŠąČąĄąĮąĖąĄ. ą×ą┤ąĮą░ą║ąŠ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ č鹊ą╗čīą║ąŠ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮčŗąĄ čāą╝ąĮąŠąČąĄąĮąĖčÅ, čéą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝ čüą┤ąĄą╗ą░ąĮ č乊ą║čāčü ąĮą░ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čü ą┐ąŠą╝ąŠčēčīčÄ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ čåąĄą╗čŗčģ čćąĖčüąĄą╗.
ą×ą▒čŗčćąĮąŠ ą┤ą╗čÅ ą▒ąŠą╗ąĄąĄ č鹊čćąĮąŠą│ąŠ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖčÅ čćąĖčüą╗ą░ ąŠąĮąŠ ą┤ąŠą╗ąČąĮąŠ ąĖą╝ąĄčéčī ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą▓ąŠąĘą╝ąŠąČąĮąŠąĄ čćąĖčüą╗ąŠ ą▒ąĖčé. ąöą╗čÅ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖčÅ ą┤čĆąŠą▒ąĮčŗčģ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ ą▓ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮčŗčģ čāą╝ąĮąŠąČąĄąĮąĖčÅčģ ą┐čĆąŠą▒ą╗ąĄą╝ą░ čüą▓ąŠą┤ąĖčéčüčÅ ą║ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÄ ą▓čüąĄčģ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čüą░ą╝čŗą╝ ą▒ąŠą╗čīčłąĖą╝ ąŠą▒čēąĖą╝ ą╝ąĮąŠąČąĖč鹥ą╗ąĄą╝, ą║ąŠč鹊čĆčŗą╣ ąĮąĄ ą▓čŗąĘčŗą▓ą░ąĄčé ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖą╣ ą▓ ąĖčģ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖąĖ. ąŁč鹊 ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ čéą░ą║ąČąĄ ą┐čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ ąĖ ą║ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčā a0, čü ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄą╝ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ ą▓čŗčģąŠą┤ą░ (ą┐ąŠ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠčüčéąĖ) ą┤ą╗čÅ ą┐ąŠą╗čāč湥ąĮąĖčÅ ą║ąŠčĆčĆąĄą║čéąĮąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ (ąŠčüąŠą▒ąĄąĮąĮąŠ ą║ą░čüą░ąĄčéčüčÅ čäąĖą╗čīčéčĆąŠą▓ IIR). ą¤ąŠčüą║ąŠą╗čīą║čā ą░ą┐ą┐ą░čĆą░čéąĮąŠąĄ ą┤ąĄą╗ąĄąĮąĖąĄ ąĮąĄą┤ąŠčüčéčāą┐ąĮąŠ, čäą░ą║č鹊čĆ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą▓ č乊čĆą╝ąĄ 2k, čéą░ą║ ą║ą░ą║ ą┤ąĄą╗ąĄąĮąĖąĄ ąĖ čāą╝ąĮąŠąČąĄąĮąĖąĄ čü ąŠčüąĮąŠą▓ą░ąĮąĖąĄą╝ 2 ą╗ąĄą│ą║ąŠ čĆąĄą░ą╗ąĖąĘčāąĄčéčüčÅ čüą┤ą▓ąĖą│ą░ą╝ąĖ. ą¤čĆąĖąĮčåąĖą┐ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ ąĖ ą┐ąŠčüą╗ąĄą┤čāčÄčēąĄą│ąŠ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ ą┐ąŠą║ą░ąĘą░ąĮ ą▓ ąŻčĆą░ą▓ąĮąĄąĮąĖąĖ 10.
ąŻčĆą░ą▓ąĮąĄąĮąĖąĄ 10: ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ čü ą┐ąŠčüą╗ąĄą┤čāčÄčēąĖą╝ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄą╝ ą▓ąĮąĖąĘ čĆąĄąĘčāą╗čīčéą░čéą░.
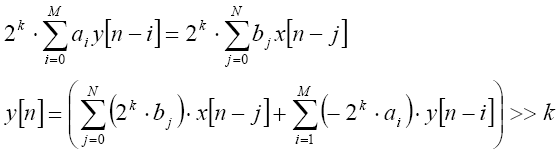
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ą▒ąĖčé ąĘąĮą░ą║ą░ (čüą░ą╝čŗą╣ čüčéą░čĆčłąĖą╣ ą▒ąĖčé) ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī čüąŠčģčĆą░ąĮąĄąĮ ą┐čĆąĖ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĖ ą▓ąĮąĖąĘ (čüą┤ą▓ąĖą│ąĄ ąĮą░ K čĆą░ąĘ ą▓ą┐čĆą░ą▓ąŠ). ą¤čĆąŠčēąĄ ą▓čüąĄą│ąŠ ą┤ą╗čÅ čŹč鹊ą╣ čåąĄą╗ąĖ ą┐čĆąĖą╝ąĄąĮąĖčéčī ąĖąĮčüčéčĆčāą║čåąĖčÄ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░ ASR (ą░čĆąĖčäą╝ąĄčéąĖč湥čüą║ąĖą╣ čüą┤ą▓ąĖą│ ą▓ą┐čĆą░ą▓ąŠ).
ąØą░ą┐čĆąĖą╝ąĄčĆ, ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ bj = {0.9001,-0.6500,0.3000}. ąĢčüą╗ąĖ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ 16-ą▒ąĖčéąĮąŠąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖąĄ čćąĖčüąĄą╗, č鹊 ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ ą┤ąŠą╗ąČąĮčŗ ą▒čŗčéčī ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ [-215..(215-1)] = [-32768..32767]. ą×ą▒čŗčćąĮąŠ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé čü čüą░ą╝čŗą╝ ą▒ąŠą╗čīčłąĖą╝ ą░ą▒čüąŠą╗čÄčéąĮčŗą╝ ąĘąĮą░č湥ąĮąĖąĄą╝ ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčé ąŠą│čĆą░ąĮąĖč湥ąĮąĖąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠą│ąŠ ą╝ąĮąŠąČąĖč鹥ą╗čÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ. ą▓ ąĮą░čłąĄą╝ čüą╗čāčćą░ąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčŗą╣ ą╝ąĮąŠąČąĖč鹥ą╗čī ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▒ąĄąĘ ą╗čÄą▒ąŠą│ąŠ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ čĆą░ą▓ąĄąĮ 215. ą×ą║čĆčāą│ą╗ąĖą▓ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ, ą┐ąŠą╗čāčćąĖą╝ ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 ąĘąĮą░č湥ąĮąĖčÅ {29494,-21299,9830} ąĖ ą┐čĆąĖą▒ą╗ąĖąĘąĖč鹥ą╗čīąĮčāčÄ ąŠčłąĖą▒ą║čā ąŠą║čĆčāą│ą╗ąĄąĮąĖčÅ ą┐čĆąĖ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĖ ą▓ąĮąĖąĘ {1.5*10-5, 6.1*10-6, 1.2*10-5}.
ą×ą┐čéąĖą╝ąĖąĘą░čåąĖčÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ ą▓ąŠąĘą╝ąŠąČąĮą░, ąĄčüą╗ąĖ čäą░ą║č鹊čĆ K ą┐čĆąĄą▓čŗčłą░ąĄčé čćąĖčüą╗ąŠ 8, čāą╝ąĮąŠąČąĄąĮąĮąŠąĄ ąĮą░ čåąĄą╗ąŠąĄ čćąĖčüą╗ąŠ (1, 2, 3, ..). ąÆ čŹč鹊ą╝ čüą╗čāčćą░ąĄ ą┐čĆąŠą│čĆą░ą╝ą╝ą░ ą┐čĆąĖ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĖ ą▓ąĮąĖąĘ ą╝ąŠąČąĄčé ą┐čĆąŠčüč鹊 ąŠčéą▒čĆą░čüčŗą▓ą░čéčī ą╝ą╗ą░ą┤čłąĖąĄ ą▒ą░ą╣čéčŗ čĆąĄąĘčāą╗čīčéą░čéą░ (1, 2, 3, .. ą▒ą░ą╣čéą░). ą¤čĆąĖą╝ąĄčĆ ą┐ąŠą║ą░ąĘą░ąĮ ąĮą░ ąĀąĖčüčāąĮą║ąĄ 3-1, ą│ą┤ąĄ 32-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī čüą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮ ą▓ąĮąĖąĘ ą▓ 2^18 čĆą░ąĘ (čé. ąĄ. čüą┤ą▓ąĖąĮčāčé ą▓ą┐čĆą░ą▓ąŠ 18 čĆą░ąĘ). ąŁč鹊 ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ ą┐čāč鹥ą╝ čüą┤ą▓ąĖą│ą░ čüčéą░čĆčłąĖčģ 16-čéąĖ ą▒ąĖčé č鹊ą╗čīą║ąŠ ą┤ą▓ą░ čĆą░ąĘą░ ą▓ą┐čĆą░ą▓ąŠ (ą┐čĆąĖ čŹč鹊ą╝ ą╝ą╗ą░ą┤čłąĖąĄ 16 ą▒ąĖčé ą┐čĆąŠčüč鹊 ąĮąĄ ą┐čĆąĖąĮąĖą╝ą░čÄčéčüčÅ ą▓ąŠ ą▓ąĮąĖą╝ą░ąĮąĖąĄ).
ąĀąĖčüčāąĮąŠą║ 3-1: ąŠą┐čéąĖą╝ąĖąĘą░čåąĖčÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ (čüąĄčĆčŗą╝ ą┐ąŠą╝ąĄč湥ąĮčŗ ąĮąĄąĖčüą┐ąŠą╗čīąĘčāąĄą╝čŗąĄ ą▒ąĖčéčŗ)

ąŁčäč乥ą║čé ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ
ą£ąŠąČąĮąŠ ąĘą░ą┤ą░čéčīčüčÅ ą▓ąŠą┐čĆąŠčüąŠą╝, ą┐ąŠč湥ą╝čā ą║ą░ąČą┤čŗą╣ čĆą░ąĘ ą╝čŗ ą┤ąŠą▒ą░ą▓ą╗čÅąĄą╝ ą▒ąĖčéčŗ, čćč鹊ą▒čŗ ąĖąĘą▒ąĄąČą░čéčī ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ą▓ ą┐ąŠą┤čĆąĄąĘčāą╗čīčéą░čéą░čģ, ą░ ąĘą░č鹥ą╝ ŌĆ£ą▓čŗą▒čĆą░čüčŗą▓ą░ąĄą╝ ąĖčģŌĆØ, čćč鹊ą▒čŗ ą▓ą╝ąĄčüčéąĖčéčī čĆąĄąĘčāą╗čīčéą░čé ą▓ čāą║ą░ąĘą░ąĮąĮąŠąĄ čĆą░ąĘčĆąĄčłąĄąĮąĖąĄ. ą×ą▒čŖčÅčüąĮąĄąĮąĖąĄ čŹč鹊ą│ąŠ "ą┐ą░čĆą░ą┤ąŠą║čüą░" čüą╗ąĄą┤čāčÄčēąĄąĄ - ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗąĄ ą▒ąĖčéčŗ ąĮą░ą╝ ąĮčāąČąĮčŗ, čćč鹊ą▒čŗ ą┐ąŠą┤ą┤ąĄčƹȹ░čéčī č鹊čćąĮąŠčüčéčī ą┐čĆąĖ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅčģ, ą░ čäąĖą╗čīčéčĆ ąĖą╝ąĄąĄčé ąĄą┤ąĖąĮąĖčćąĮąŠąĄ čāčüąĖą╗ąĄąĮąĖąĄ, ą┐čĆąĖ čŹč鹊ą╝ ąĄą│ąŠ ą▓čŗčģąŠą┤ąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ čüąĖą│ąĮą░ą╗ą░ ą┤ąŠą╗ąČąĮčŗ ąĖąĮč鹥čĆą┐čĆąĄčéąĖčĆąŠą▓ą░čéčīčüčÅ ą║ą░ą║ čåąĄą╗čŗąĄ čćąĖčüą╗ą░.
ąöą╗čÅ čäąĖą╗čīčéčĆąŠą▓ čü ąĄą┤ąĖąĮąĖčćąĮčŗą╝ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą╝ ą┐ąĄčĆąĄą┤ą░čćąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ (ai, bj) ą▒čāą┤čāčé ą┤čĆąŠą▒ąĮčŗą╝ąĖ čćąĖčüą╗ą░ą╝ąĖ, ą╝ąĄąĮčīčłąĖą╝ąĖ, č湥ą╝ ąĄą┤ąĖąĮąĖčåą░. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ą┤ąŠą╝ąĮąŠąČąĄąĮąĖąĄ ą┐čĆąĖ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĖ ą┐čĆąŠčüč鹊 ą┤ąŠą▒ą░ą▓ą╗čÅąĄčé ą▒ąĖčéčŗ, ą║ąŠč鹊čĆčŗąĄ ą▒čāą┤čāčé ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅčéčī ą┤čĆąŠą▒ąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ. ąĪčāą╝ą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ, ąŠą┤ąĮą░ą║ąŠ, ą┤ąŠą▒ą░ą▓ąĖčé ą▒ąĖčéčŗ, ą║ąŠč鹊čĆčŗąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅčÄčé ą▒ąŠą╗ąĄąĄ ą▓čŗčüąŠą║ąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ. ąØąŠ ąĖąĘ-ąĘą░ ąĄą┤ąĖąĮąĖčćąĮąŠą│ąŠ čāčüąĖą╗ąĄąĮąĖčÅ čäąĖą╗čīčéčĆą░, čŹčéąĖ ą▒ąĖčéčŗ ąĮąĖą║ąŠą│ą┤ą░ ąĮąĄ ą▒čāą┤čāčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ą▓ čĆąĄąĘčāą╗čīčéą░č鹥: ą▓čŗčģąŠą┤ čäąĖą╗čīčéčĆą░ ąĮąĄ ą┐ąŠą╗čāčćąĖčé ą░ą▒čüąŠą╗čÄčéąĮčāčÄ ą▓ąĄą╗ąĖčćąĖąĮčā čüąĖą│ąĮą░ą╗ą░ ą▒ąŠą╗čīčłąĄ, č湥ą╝ ą▓ąĄą╗ąĖčćąĖąĮą░ čüąĖą│ąĮą░ą╗ą░ ąĮą░ ą▓čģąŠą┤ąĄ, čćč鹊 ą┐ąŠąĘą▓ąŠą╗čÅąĄčé ą▓čŗčģąŠą┤čā ą▒čŗčéčī ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĮčŗą╝ čü č鹥ą╝ ąČąĄ čüą░ą╝čŗą╝ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮčŗą╝ ą┤ąĖą░ą┐ą░ąĘąŠąĮąŠą╝, ą║ą░ą║ ąĖ ą▓čģąŠą┤.
ą£ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ ą▓ąĮąĖąĘ ą┐čĆąŠčüč鹊 čāą┤ą░ą╗čÅąĄčé ą┤čĆąŠą▒ąĮčāčÄ čćą░čüčéčī čĆąĄąĘčāą╗čīčéą░čéą░, ąŠčüčéą░ą▓ą╗čÅčÅ č鹊ą╗čīą║ąŠ čåąĄą╗čāčÄ čćą░čüčéčī čü čéčĆąĄą▒čāąĄą╝ąŠą╣ č鹊čćąĮąŠčüčéčīčÄ (ą║ąŠą╗ąĖč湥čüčéą▓ąŠą╝ ą▒ąĖčé). ą»čüąĮąŠ, čćč鹊 čŹč鹊 čéą░ą║ąČąĄ ąŠąĘąĮą░čćą░ąĄčé - č鹊čćąĮąŠčüčéčī čāą╝ąĄąĮčīčłą░ąĄčéčüčÅ. ąŁč鹊 ą▓ą░ąČąĮąŠ ą┤ą╗čÅ IIR-čäąĖą╗čīčéčĆąŠą▓, čéą░ą║ ą║ą░ą║ čā ąĮąĖčģ ąĄčüčéčī ąŠą▒čĆą░čéąĮą░čÅ čüą▓čÅąĘčī. ąĢčüą╗ąĖ čŹčäč乥ą║čé ąŠčé ą┐ąŠč鹥čĆąĖ č鹊čćąĮąŠčüčéąĖ ąĘą┤ąĄčüčī čüąŠąĘą┤ą░ąĄčé ą┐čĆąŠą▒ą╗ąĄą╝čā, č鹊 ą┐ąŠč鹥čĆčÅ č鹊čćąĮąŠčüčéąĖ ą╝ąŠąČąĄčé ą▒čŗčéčī čāą╝ąĄąĮčīčłąĄąĮą░ ą┤ą▓čāą╝čÅ čüą┐ąŠčüąŠą▒ą░ą╝ąĖ:
- čüą┤ąĄą╗ą░čéčī čāčüąĖą╗ąĄąĮąĖąĄ čäąĖą╗čīčéčĆą░ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčŗą╝, ą┐čĆąĖ čŹč鹊ą╝ ą▓čŗčģąŠą┤ ą▒čāą┤ąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī ą▓ąĄčüčī ą┤ąŠčüčéčāą┐ąĮčŗą╣ ą┤ąĖą░ą┐ą░ąĘąŠąĮ ąĘąĮą░č湥ąĮąĖą╣.
- čāą▓ąĄą╗ąĖčćąĖčéčī ąŠą┤ąĮąŠą▓čĆąĄą╝ąĄąĮąĮąŠ ąĖ č鹊čćąĮąŠčüčéčī ą▓čŗčģąŠą┤ą░ ąĖ čāčüąĖą╗ąĄąĮąĖąĄ čäąĖą╗čīčéčĆą░.
ąĢčüą╗ąĖ ą┐čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ ą▓č鹊čĆąŠą╣ ą╝ąĄč鹊ą┤, č鹊 ą┐ąŠčüą╗ąĄą┤ąĮąĖą╣ čäą░ą║č鹊čĆ ą╝ąŠąČąĄčé ą▓ą╗ąĖčÅčéčī ąĮą░ čĆą░ąĘą╝ąĄčĆ ą║ąŠą┤ą░ ąĖ ą┐čĆąŠą┐čāčüą║ąĮčāčÄ čüą┐ąŠčüąŠą▒ąĮąŠčüčéčī, čéą░ą║ ą║ą░ą║ ą╝ąŠąČąĄčé ą┐ąŠčéčĆąĄą▒ąŠą▓ą░čéčīčüčÅ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ čāą▓ąĄą╗ąĖč湥ąĮąĮąŠą│ąŠ čĆą░ąĘą╝ąĄčĆą░.
ąŻą╝ąĄąĮčīčłąĄąĮąĮą░čÅ č鹊čćąĮąŠčüčéčī čü čåąĄą╗čīčÄ ą┐ąŠą▓čŗčłąĄąĮąĖčÅ ą┐čĆąŠą┐čāčüą║ąĮąŠą╣ čüą┐ąŠčüąŠą▒ąĮąŠčüčéąĖ
ą¦č鹊ą▒čŗ čāčüą║ąŠčĆąĖčéčī čĆą░ą▒ąŠčéčā ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░čåąĖąĖ, ą╝ąŠąČąĄčé ą┐ąŠčéčĆąĄą▒ąŠą▓ą░čéčīčüčÅ čāą╝ąĄąĮčīčłąĖčéčī č鹊čćąĮąŠčüčéčī ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ ąĖ/ąĖą╗ąĖ ą▓čģąŠą┤ąĮčŗčģ ą▓čŗą▒ąŠčĆąŠą║ čüąĖą│ąĮą░ą╗ą░, čćč鹊 ą┐ąŠąĘą▓ąŠą╗ąĖčé čāą╝ąĄąĮčīčłąĖčéčī čĆą░ąĘą╝ąĄčĆ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░. ąŻą╝ąĄąĮčīčłąĄąĮąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ ąŠąĘąĮą░čćą░ąĄčé, čćč鹊 ą░ą╗ą│ąŠčĆąĖčéą╝ ą┐ąŠčéčĆąĄą▒čāąĄčé ą╝ąĄąĮčīčłąĄ ąŠą┐ąĄčĆą░čåąĖą╣ ąĮą░ čāą╝ąĮąŠąČąĄąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ čäąĖą╗čīčéčĆą░ ąĖ ą▓čŗą▒ąŠčĆą║ąĖ. ą×ą┤ąĮą░ą║ąŠ, ą┐čĆąĄąČą┤ąĄ č湥ą╝ čāą╝ąĄąĮčīčłą░čéčī č鹊čćąĮąŠčüčéčī, ąĮčāąČąĮąŠ ą┐čĆąĖąĮčÅčéčī ą▓ąŠ ą▓ąĮąĖą╝ą░ąĮąĖąĄ ą┤ą▓ą░ ą╝ąŠą╝ąĄąĮčéą░:
- čāą╝ąĄąĮčīčłąĄąĮąĖąĄ č鹊čćąĮąŠčüčéąĖ ą▓čģąŠą┤ąĮčŗčģ ą▓čŗą▒ąŠčĆąŠą║ ąŠąĘąĮą░čćą░ąĄčé ą┤ąŠą▒ą░ą▓ą╗ąĄąĮąĖąĄ čłčāą╝ą░ ą▓ čüąĖčüč鹥ą╝čā, čćč鹊 ąŠą▒čŗčćąĮąŠ ąĮąĄąČąĄą╗ą░č鹥ą╗čīąĮąŠ.
- čāą╝ąĄąĮčīčłąĄąĮąĖąĄ č鹊čćąĮąŠčüčéąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ ąŠąĘąĮą░čćą░ąĄčé, čćč鹊 ąĮčāąČąĮčāčÄ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║čā čäąĖą╗čīčéčĆą░ ą┐ąŠą╗čāčćąĖčéčī ą▒čāą┤ąĄčé čüą╗ąŠąČąĮąĄąĄ.
ąöčĆčāą│ąĖąĄ ą╝ąĄč鹊ą┤čŗ ą┐ąŠą▓čŗčłąĄąĮąĖčÅ ą┐čĆąŠą┐čāčüą║ąĮąŠą╣ čüą┐ąŠčüąŠą▒ąĮąŠčüčéąĖ čüą╝. ą▓ čĆą░ąĘą┤ąĄą╗ąĄ "ą×ą┐čéąĖą╝ąĖąĘą░čåąĖčÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░".
[4. ąĀąĄą░ą╗ąĖąĘą░čåąĖčÅ čäąĖą╗čīčéčĆą░]
ą¤čĆąĖą╝ąĄčĆčŗ čäąĖą╗čīčéčĆąŠą▓ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ čĆą░ąĘčĆą░ą▒ąŠčéą░ąĮčŗ ąĖ čüą║ąŠą╝ą┐ąĖą╗ąĖčĆąŠą▓ą░ąĮčŗ ą▓ čüčĆąĄą┤ąĄ ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆą░ IAR EWAVR ą▓ąĄčĆčüąĖąĖ 5.03A.
ąÜąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ ą▓čŗčćąĖčüą╗ąĄąĮčŗ čü ą┐ąŠą╝ąŠčēčīčÄ čüą┐ąĄčåąĖą░ą╗čīąĮąŠą│ąŠ ą┐čĆąŠą│čĆą░ą╝ą╝ąĮąŠą│ąŠ ąŠą▒ąĄčüą┐ąĄč湥ąĮąĖčÅ. ąöą╗čÅ čŹč鹊ą│ąŠ ąĖą╝ąĄąĄčéčüčÅ ą╝ąĮąŠąČąĄčüčéą▓ąŠ ą┐čĆąŠą│čĆą░ą╝ą╝, ąĮą░čćąĖąĮą░čÅ ąŠčé ą┤ąŠčĆąŠą│ąĖčģ čéąĖą┐ą░ Matlab, ą║ąŠąĮčćą░čÅ ą▒ąĄčüą┐ą╗ą░čéąĮčŗą╝ąĖ ą░ą┐ą┐ą╗ąĄčéą░ą╝ąĖ Java, ą┤ąŠčüčéčāą┐ąĮčŗą╝ąĖ č湥čĆąĄąĘ web. ąĪą┐ąĖčüąŠą║ web-čüą░ą╣č鹊ą▓, ą║ąŠč鹊čĆčŗąĄ ąĖą╝ąĄčÄčé ą┤ąĄą╗ąŠ čü č鹥ą╝ąŠą╣ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅą╝ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░, ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗ąĄąĮ ą▓ ą╗ąĖč鹥čĆą░čéčāčĆąĮąŠą╝ čüą┐ąĖčüą║ąĄ ą▓ ą║ąŠąĮčåąĄ čüčéą░čéčīąĖ. ąÉą╗čīč鹥čĆąĮą░čéąĖą▓ąŠą╣ ą╝ąŠąČąĄčé ą▒čŗčéčī ą▓čŗčćąĖčüą╗ąĄąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ "čéčĆčāą┤ąĮčŗą╝" ą┐čāč鹥ą╝ - ą▓čĆčāčćąĮčāčÄ. ą£ąĄč鹊ą┤čŗ ą┤ą╗čÅ čĆą░čüč湥čéą░ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ (ąĖ ą┤ąŠčüčéąĖąČąĄąĮąĖčÅ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéąĖ čŹčéąĖčģ čäąĖą╗čīčéčĆąŠą▓) ąŠą┐ąĖčüą░ąĮčŗ ą▓ [1] ąĖ [2].
ąÆ ą┐čĆąĖą╝ąĄčĆą░čģ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮčŗ ą┤ą▓ą░ čäąĖą╗čīčéčĆą░ - čäąĖą╗čīčéčĆ ą▓ąĄčĆčģąĮąĖčģ čćą░čüč鹊čé (High Pass, HP) FIR-čäąĖą╗čīčéčĆ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░, ąĖ ą┐ąŠą╗ąŠčüąŠą▓ąŠą╣ čäąĖą╗čīčéčĆ (Band Pass, BP) IIR-čäąĖą╗čīčéčĆ 2-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░. ąÆ ąŠą▒ąĄąĖčģ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅčģ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ 10-ą▒ąĖčéąĮčŗąĄ čüąŠ ąĘąĮą░ą║ąŠą╝ ąŠčéčüč湥čéčŗ čüąĖą│ąĮą░ą╗ą░ ąĮą░ ą▓čģąŠą┤ąĄ (čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī ąÉą”ą¤ AVR 10 ą▒ąĖčé). FIR-čäąĖą╗čīčéčĆ ąĖčüą┐ąŠą╗čīąĘčāąĄčé 13-ą▒ąĖčéąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čüąŠ ąĘąĮą░ą║ąŠą╝, IIR-čäąĖą╗čīčéčĆ ąĖčüą┐ąŠą╗čīąĘčāąĄčé 12-ą▒ąĖčéąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čüąŠ ąĘąĮą░ą║ąŠą╝. ąŁč鹊 čéčĆąĄą▒čāąĄčé ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠą│ąŠ čĆą░ąĘą╝ąĄčĆą░ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░ 24 ą▒ąĖčéą░.
ążąĖą╗čīčéčĆčŗ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮčŗ ąĮą░ ą░čüčüąĄą╝ą▒ą╗ąĄčĆąĄ ą┐ąŠ čüąŠąŠą▒čĆą░ąČąĄąĮąĖčÅą╝ čŹčäč乥ą║čéąĖą▓ąĮąŠčüčéąĖ. ąĀąĄą░ą╗ąĖąĘą░čåąĖčÅ ą▓čŗą┐ąŠą╗ąĮąĄąĮą░ čéą░ą║, čćč鹊 čäčāąĮą║čåąĖąĖ čäąĖą╗čīčéčĆą░ ą╝ąŠąČąĮąŠ ą▓čŗąĘčŗą▓ą░čéčī ąĖąĘ ą║ąŠą┤ą░ ąĮą░ C. ą¤ąĄčĆąĄą┤ ą▓čŗąĘąŠą▓ąŠą╝ čäčāąĮą║čåąĖą╣ čäąĖą╗čīčéčĆą░ čéčĆąĄą▒čāąĄčéčüčÅ ąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░čéčī čāąĘą╗čŗ čäąĖą╗čīčéčĆą░ (ą┐ą░ą╝čÅčéčī ąĖ 菹╗ąĄą╝ąĄąĮčéčŗ ąĘą░ą┤ąĄčƹȹ║ąĖ) - ąĖąĮą░č湥 ąĮą░čćą░ą╗čīąĮčŗąĄ čāčüą╗ąŠą▓ąĖčÅ ą┤ą╗čÅ čĆą░ą▒ąŠčéčŗ čäąĖą╗čīčéčĆą░ ą▒čāą┤čāčé ąĮąĄąĖąĘą▓ąĄčüčéąĮčŗ. ąöą╗čÅ ąŠą▒ąŠąĖčģ čäąĖą╗čīčéčĆąŠą▓ ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą┐čĆąĖą╝ąĄčĆ ą║ąŠą┤ą░ ąĮą░ C, ąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆčāčÄčēąĄą│ąŠ ąĖ ą▓čŗąĘčŗą▓ą░čÄčēąĄą│ąŠ ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗ąĄąĮąĮčŗąĄ čäčāąĮą║čåąĖąĖ čäąĖą╗čīčéčĆą░.
ąÆčüąĄ ą┐ą░čĆą░ą╝ąĄčéčĆčŗ, čéčĆąĄą▒čāąĄą╝čŗąĄ ą┤ą╗čÅ čäąĖą╗čīčéčĆą░čåąĖąĖ, ą┐ąĄčĆąĄą┤ą░čÄčéčüčÅ ą▓ąŠ ą▓čĆąĄą╝čÅ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ, ą┐ąŠčŹč鹊ą╝čā čäčāąĮą║čåąĖąĖ ą╝ąŠą│čāčé ą▒čŗčéčī ą┐ąŠą▓č鹊čĆąĮąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮčŗ ą┤ą╗čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ą▒ąŠą╗ąĄąĄ č湥ą╝ ąŠą┤ąĮąŠą│ąŠ čäąĖą╗čīčéčĆą░ ą▒ąĄąĘ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ ąĘą░čéčĆą░čé ą╝ąĄčüčéą░ ą┐ąŠą┤ ą║ąŠą┤. ąŁč鹊 ą╝ąŠąČąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ą┤ą╗čÅ ą║ą░čüą║ą░ą┤ąĮąŠą│ąŠ čüąŠąĄą┤ąĖąĮąĄąĮąĖčÅ čäąĖą╗čīčéčĆąŠą▓ - čćą░čüč鹊 ąĮąĄčüą║ąŠą╗čīą║ąŠ čäąĖą╗čīčéčĆąŠą▓ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░ ą▓ą║ą╗čÄčćą░čÄčéčüčÅ ą┤čĆčāą│ ąĘą░ ą┤čĆčāą│ąŠą╝ (ą▓čŗčģąŠą┤ ąŠą┤ąĮąŠą│ąŠ čäąĖą╗čīčéčĆą░ čüąŠ ą▓čģąŠą┤ąŠą╝ ą┤čĆčāą│ąŠą│ąŠ) ą┤ą╗čÅ ą┐ąŠą╗čāč湥ąĮąĖčÅ čäąĖą╗čīčéčĆą░ ą▒ąŠą╗ąĄąĄ ą▓čŗčüąŠą║ąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░. ą×ą┤ąĮą░ą║ąŠ, čéą░ą║ ą║ą░ą║ ą▓čŗčģąŠą┤ ą║ą░ąČą┤ąŠą│ąŠ ąĖąĘ čäąĖą╗čīčéčĆąŠą▓ ą▓ ą║ą░čüą║ą░ą┤ąĄ ą╝ą░čüčłčéą░ą▒ąĖčĆčāąĄčéčüčÅ ą▓ąĮąĖąĘ ą┐ąĄčĆąĄą┤ ą┐ąŠą┐ą░ą┤ą░ąĮąĖąĄą╝ ąĮą░ ą▓čģąŠą┤ ą┤čĆčāą│ąŠą│ąŠ čäąĖą╗čīčéčĆą░, č鹊 ąĮą░ ą▓čŗčģąŠą┤ąĄ čĆąĄąĘčāą╗čīčéąĖčĆčāčÄčēąĄą│ąŠ čäąĖą╗čīčéčĆą░ ą╝ąŠąČąĄčé ąŠą║ą░ąĘą░čéčīčüčÅ čüąŠą▓čüąĄą╝ ąĮąĄ č鹊, čćč鹊 ąŠąČąĖą┤ą░ą╗ąŠčüčī. ąŁč鹊 ą┐čĆąŠąĖčüčģąŠą┤ąĖčé ą┐ąŠč鹊ą╝čā, čćč鹊 č鹥čĆčÅąĄčéčüčÅ č鹊čćąĮąŠčüčéčī ą╝ąĄąČą┤čā ą║ą░čüą║ą░ą┤ą░ą╝ąĖ čäąĖą╗čīčéčĆąŠą▓. ąĢčüč鹥čüčéą▓ąĄąĮąĮąŠ, čŹčäč乥ą║čé čŹč鹊ą│ąŠ čüčéą░ąĮąŠą▓ąĖčéčüčÅ ą▒ąŠą╗ąĄąĄ čÅą▓ąĮčŗą╝ čü čāą▓ąĄą╗ąĖč湥ąĮąĖąĄą╝ ą║ąŠą╗ąĖč湥čüčéą▓ą░ ąĘą▓ąĄąĮčīąĄą▓ ą▓ ą║ą░čüą║ą░ą┤ąĮąŠą╝ čäąĖą╗čīčéčĆąĄ.
ąĀąĄą░ą╗ąĖąĘą░čåąĖčÅ čäąĖą╗čīčéčĆąŠą▓ čüą┤ąĄą╗ą░ąĮą░ čü č乊ą║čāčüąŠą╝ ąĮą░ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖąĄ, ą┐ąŠčüą║ąŠą╗čīą║čā ąŠč湥ąĮčī ą▓ą░ąČąĮą░ ą▓čŗčüąŠą║ą░čÅ ą┐čĆąŠą┐čāčüą║ąĮą░čÅ čüą┐ąŠčüąŠą▒ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░. ąĪą╝. čĆą░ąĘą┤ąĄą╗ "ą×ą┐čéąĖą╝ąĖąĘą░čåąĖčÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░", ą│ą┤ąĄ čĆą░ąĘą╝ąĄčēąĄąĮčŗ čüąŠą▓ąĄčéčŗ ą┐ąŠ čāą╝ąĄąĮčīčłąĄąĮąĖčÄ čĆą░ąĘą╝ąĄčĆą░ ą║ąŠą┤ą░, čāą▓ąĄą╗ąĖč湥ąĮąĖčÄ ą┐čĆąŠą┐čāčüą║ąĮąŠą╣ čüą┐ąŠčüąŠą▒ąĮąŠčüčéąĖ, 菹║ąŠąĮąŠą╝ąĖąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ą┐ą░ą╝čÅčéąĖ.
4.1 FIR-čäąĖą╗čīčéčĆ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
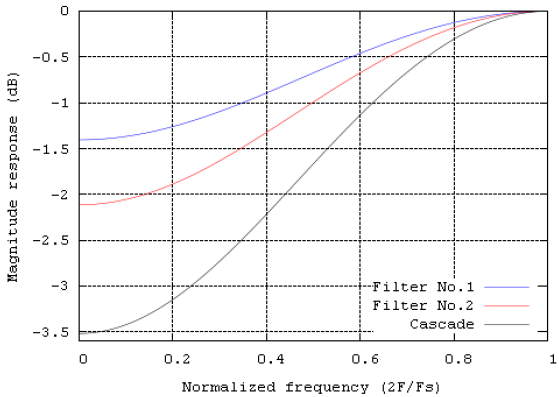
ą¦č鹊ą▒čŗ ą┐čĆąŠą┤ąĄą╝ąŠąĮčüčéčĆąĖčĆąŠą▓ą░čéčī č鹥čģąĮąĖą║čā ą║ą░čüą║ą░ą┤ąĖčĆąŠą▓ą░ąĮąĖčÅ, čŹč鹊čé čäąĖą╗čīčéčĆ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮ ą┐čāč鹥ą╝ čüąŠąĄą┤ąĖąĮąĄąĮąĖčÅ ą┤ą▓čāčģ HP čäąĖą╗čīčéčĆąŠą▓ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░. ą×ą▒ą░ čäąĖą╗čīčéčĆą░ čüą┤ąĄą╗ą░ąĮčŗ ą┐ąŠ č鹥čģąĮąĖą║ąĄ ąŠą║ąĮą░, ąŠą┐ąĖčüą░ąĮąĮąŠą╣ ą▓ [1], ą┐čĆąĖą╝ąĄąĮąĄąĮąŠ ąŠą║ąĮąŠ ąźąĄą╝ą╝ąĖąĮą│ą░ (Hamming window). ą¤ą░čĆą░ą╝ąĄčéčĆčŗ čäąĖą╗čīčéčĆą░ ą┐ąŠą║ą░ąĘą░ąĮčŗ ą▓ ąóą░ą▒ą╗ąĖčåąĄ 4-1. ąĀąĖčüčāąĮąŠą║ 4-1 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą░ą╝ą┐ą╗ąĖčéčāą┤ąĮčāčÄ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║čā ąŠą▒ąŠąĖčģ čäąĖą╗čīčéčĆąŠą▓ ą┐ąŠ ąŠčéą┤ąĄą╗čīąĮąŠčüčéąĖ, ąĖ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║čā ąĖčģ ą║ą░čüą║ą░ą┤ąĖčĆąŠą▓ą░ąĮąĖčÅ.
ąóą░ą▒ą╗ąĖčåą░ 4-1: ą┐ą░čĆą░ą╝ąĄčéčĆčŗ HP FIR-čäąĖą╗čīčéčĆą░ 2-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
ążąĖą╗čīčéčĆ
|
ą¤ąŠčĆčÅą┤ąŠą║
|
ąĪčĆąĄąĘ
|
ąÜąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ (b0,b1,b2)
|
ą£ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ
|
ąĪą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ (b0,b1,b2) |
| 1 |
2 |
0.4 |
-0.0373, 0.9253, -0.0373 |
212 |
-153, 3790, -153 |
| 2 |
2 |
0.6 |
-0.0540, 0.8920, -0.0540 |
212 |
-222, 3653, -222 |
ąĀąĖčüčāąĮąŠą║ 4-1: ąÉą¦ąź FIR-čäąĖą╗čīčéčĆąŠą▓
ą¤ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ čäąĖą╗čīčéčĆąŠą▓ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮčŗ ąĮą░ ą░čüčüąĄą╝ą▒ą╗ąĄčĆąĄ ą┤ą╗čÅ ą┐ąŠą╗čāč湥ąĮąĖčÅ čŹčäč乥ą║čéąĖą▓ąĮąŠą│ąŠ ą║ąŠą┤ą░. ą×ą┤ąĮą░ą║ąŠ ą┐ą░čĆą░ą╝ąĄčéčĆčŗ čäąĖą╗čīčéčĆą░ ąĖ čāąĘą╗čŗ čäąĖą╗čīčéčĆą░ ą┐čĆąĄą┤ą▓ą░čĆąĖč鹥ą╗čīąĮąŠ (ą┤ąŠ ą▓čŗąĘąŠą▓ą░ čäčāąĮą║čåąĖąĖ čäąĖą╗čīčéčĆą░čåąĖąĖ) ą┤ąŠą╗ąČąĮčŗ ą▒čŗčéčī ą┐čĆąŠąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮčŗ ą┐čĆąŠą│čĆą░ą╝ą╝ąŠą╣ ąĮą░ čÅąĘčŗą║ąĄ C. ąĪčéčĆčāą║čéčāčĆą░ čüąŠą┤ąĄčƹȹĖčé ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ ąĖ čāąĘą╗čŗ čäąĖą╗čīčéčĆą░, ą║ąŠč鹊čĆčŗąĄ ąĘą░ą┤ą░čÄčéčüčÅ ą┤ą╗čÅ ą║ą░ąČą┤ąŠą│ąŠ čäąĖą╗čīčéčĆą░ ąŠčéą┤ąĄą╗čīąĮąŠ. ąĪčéčĆčāą║čéčāčĆčŗ ąĘą░ą┤ą░ąĮčŗ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝:
struct FIR_filter
{
int filterNodes [FILTER_ORDER]; //ą┐ą░ą╝čÅčéčī ą┤ą╗čÅ čāąĘą╗ąŠą▓ čäąĖą╗čīčéčĆą░
int filterCoefficients[FILTER_ORDER+1]; //ą┐ą░ą╝čÅčéčī ą┤ą╗čÅ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░
} filter04 = {0,0, B10, B11, B12}, //ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÅ 1-ą│ąŠ čäąĖą╗čīčéčĆą░
filter06 = {0,0, B20, B21, B22}; //ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÅ 2-ą│ąŠ čäąĖą╗čīčéčĆą░
ą£ą░čüčüąĖą▓ filterNodes ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą║ą░ą║ ą▒čāč乥čĆ FIFO, ą▓ ą║ąŠč鹊čĆąŠą╝ čüąŠčģčĆą░ąĮčÅčÄčéčüčÅ ą┐čĆąĄą┤čŗą┤čāčēąĖąĄ ąĘąĮą░č湥ąĮąĖčÅ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░. ą£ą░čüčüąĖą▓ filterCoefficients ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ feedforward-ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ (bj) čäąĖą╗čīčéčĆą░. ą¤ąŠčüą╗ąĄ č鹊ą│ąŠ, ą║ą░ą║ čäąĖą╗čīčéčĆ ą┐čĆąŠąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮ, ą╝ąŠąČąĄčé ą▒čŗčéčī ą▓čŗąĘą▓ą░ąĮą░ čäčāąĮą║čåąĖčÅ čäąĖą╗čīčéčĆą░. ążčāąĮą║čåąĖčÅ čäąĖą╗čīčéčĆą░ ąĘą░ą┤ą░ąĮą░ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝:
int FIR2(struct FIR_filter *myFilter, int newSample);
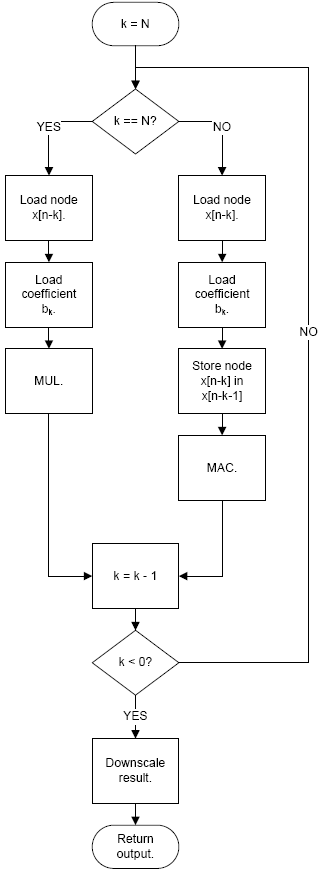
ąĪąĮą░čćą░ą╗ą░ čäčāąĮą║čåąĖčÅ ą║ąŠą┐ąĖčĆčāąĄčé čāą║ą░ąĘą░č鹥ą╗čī ąĮą░ čüčéčĆčāą║čéčāčĆčā FIR_filter ą▓ Z-čĆąĄą│ąĖčüčéčĆ, ą┐ąŠčüą║ąŠą╗čīą║čā ąŠąĮ ą╝ąŠąČąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ąĮąĄą┐čĆčÅą╝ąŠą╣ (indirect) ą░ą┤čĆąĄčüą░čåąĖąĖ ą┤ą░ąĮąĮčŗčģ, ąĮą░ą┐čĆąĖą╝ąĄčĆ ą┤ą╗čÅ ąŠą┐ąĄčĆą░čåąĖą╣ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čāą║ą░ąĘą░č鹥ą╗čÅ. ąŚą░č鹥ą╝ ąŠčüąĮąŠą▓ąĮąŠą╣ ą░ą╗ą│ąŠčĆąĖčéą╝ ą│ąŠč鹊ą▓ ą║ ąĘą░ą┐čāčüą║čā. ąÆčŗą▒ąŠčĆą║ąĖ (čāąĘą╗čŗ čäąĖą╗čīčéčĆą░) ąĘą░ą│čĆčāąČą░čÄčéčüčÅ ąĖ čāą╝ąĮąŠąČą░čÄčéčüčÅ (ąĖąĮčüčéčĆčāą║čåąĖąĄą╣ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░ MUL) čü čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĖą╝ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ą╝ąĖ. ąĀąĄąĘčāą╗čīčéą░čéčŗ ą┤ąŠą▒ą░ą▓ą╗čÅčÄčéčüčÅ ą▓ 24-ą▒ąĖčéąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ. ąÜąŠą│ą┤ą░ ą▓čüąĄ ą▓čŗą▒ąŠčĆą║ąĖ ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čāą╝ąĮąŠąČąĄąĮčŗ ąĖ čüąŠčģčĆą░ąĮąĄąĮčŗ (multiplied-and-accumulated, ąŠą┐ąĄčĆą░čåąĖčÅ MAC), čĆąĄąĘčāą╗čīčéą░čé ą╝ą░čüčłčéą░ą▒ąĖčĆčāąĄčéčüčÅ ą▓ąĮąĖąĘ ąĖ ą▓ąŠąĘą▓čĆą░čēą░ąĄčéčüčÅ. ą¤čĆąŠčåąĄčüčü ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ą╝ąŠąČąĮąŠ čāą▓ąĖą┤ąĄčéčī ąĮą░ ąĀąĖčüčāąĮą║ąĄ 4-2, ą║ąŠč鹊čĆčŗą╣ ąŠą┐ąĖčüčŗą▓ą░ąĄčé ą┤ąĄą╣čüčéą▓ąĖčÅ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░ FIR.
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ąĮąĄčüą╝ąŠčéčĆčÅ ąĮą░ č鹊, čćč鹊 ą┤ąĖą░ą│čĆą░ą╝ą╝ą░ ąĮą░ ąĀąĖčüčāąĮą║ąĄ 4-2 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą░ą╗ą│ąŠčĆąĖčéą╝, čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąĮčŗą╣ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čåąĖą║ą╗ąŠą▓, ąĮą░ čüą░ą╝ąŠą╝ ą┤ąĄą╗ąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮ ą╗ąĖąĮąĄą╣ąĮčŗą╝ ą║ąŠą┤ąŠą╝ (ą┤ą╗čÅ čāą▓ąĄą╗ąĖč湥ąĮąĖčÅ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ). ą”ąĖą║ą╗ ąĮą░ ą┤ąĖą░ą│čĆą░ą╝ą╝ąĄ ą┐čĆąŠčüč鹊 ą┐čĆąĖą╝ąĄąĮąĄąĮ ą┤ą╗čÅ čāą╗čāčćčłąĄąĮąĖčÅ čćąĖčéą░ąĄą╝ąŠčüčéąĖ ą░ą╗ą│ąŠčĆąĖčéą╝ą░.
ąĀąĖčüčāąĮąŠą║ 4-2: Generic (čéčĆą░ą┤ąĖčåąĖąŠąĮąĮčŗą╣) ą░ą╗ą│ąŠčĆąĖčéą╝ FIR-čäąĖą╗čīčéčĆą░
ąÜą░ą║ čüąŠąŠą▒čēą░ą╗ąŠčüčī čĆą░ąĮąĄąĄ, ą┤ą▓ą░ čäąĖą╗čīčéčĆą░ ą▓ą║ą╗čÄč湥ąĮčŗ ą║ą░čüą║ą░ą┤ąĮąŠ. ąÆ ą╝ąŠą┤čāą╗ąĄ ąĮą░ čÅąĘčŗą║ąĄ C čŹč鹊 ą┤ąĄą╗ą░ąĄčéčüčÅ ą┐čĆąŠčüč鹊 ą┐čāč鹥ą╝ ą┐ąĄčĆąĄą┤ą░čćąĖ čäąĖą╗čīčéčĆčā 1 č湥čĆąĄąĘ ą░čĆą│čāą╝ąĄąĮčé ą▓čģąŠą┤ąĮąŠą╣ ą▓čŗą▒ąŠčĆą║ąĖ, ąĖ ąĘą░č鹥ą╝ ą┐čāč鹥ą╝ ą┐ąĄčĆąĄą┤ą░čćąĖ čäąĖą╗čīčéčĆčā 2 ą▓ ą║ą░č湥čüčéą▓ąĄ ą▓čģąŠą┤ąĮąŠą│ąŠ ą░čĆą│čāą╝ąĄąĮčéą░ čĆąĄąĘčāą╗čīčéą░čéą░ čäąĖą╗čīčéčĆą░ 1. ąÜą░ąČą┤čŗą╣ čĆą░ąĘ ą▓čŗąĘčŗą▓ą░ąĄčéčüčÅ čéą░ ąČąĄ čüą░ą╝ą░čÅ čäčāąĮą║čåąĖčÅ - ąĖ ą┤ą╗čÅ čäąĖą╗čīčéčĆą░ 1, ąĖ ą┤ą╗čÅ čäąĖą╗čīčéčĆą░ 2.
4.1.1 ąĪą║ąŠčĆąŠčüčéčī čĆą░ą▒ąŠčéčŗ FIR-čäąĖą╗čīčéčĆą░
ąóą░ą▒ą╗ąĖčåą░ 4-2 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖąĄ ąŠą┤ąĮąŠą│ąŠ ąĘą▓ąĄąĮą░ - FIR-čäąĖą╗čīčéčĆą░ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░. ąŚąĮą░č湥ąĮąĖąĄ čüč湥čéčćąĖą║ą░ ą▓ čéą░ą▒ą╗ąĖčåąĄ ą┐ąŠą║ą░ąĘčŗą▓ą░čÄčé ąĘą░čéčĆą░čéčŗ ą▓čĆąĄą╝ąĄąĮąĖ (ą▓ čåąĖą║ą╗ą░čģ čÅą┤čĆą░ AVR) ąĮą░ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░ (ąŠą┐ąĄčĆą░čåąĖąĖ MUL ąĖ MAC, ąŠą▒ąĮąŠą▓ą╗ąĄąĮąĖąĄ čāąĘą╗ąŠą▓), ą░ čéą░ą║ąČąĄ ąĮą░ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčāčÄ ąŠą▒čĆą░ą▒ąŠčéą║čā ą┐čĆąĖ ąĘą░ą▓ąĄčĆčłąĄąĮąĖąĖ čäčāąĮą║čåąĖąĖ (ą▓ą║ą╗čÄčćą░čÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ ą▓ąĮąĖąĘ). ąÆčĆąĄą╝čÅ, ąĘą░čéčĆą░č湥ąĮąĮąŠąĄ ąĮą░ ą▓čŗąĘąŠą▓čŗ (call) ąĖ ą▓ąŠąĘą▓čĆą░čé ąĖąĘ čäčāąĮą║čåąĖąĖ (return), ą▓ čéą░ą▒ą╗ąĖčåąĄ ąĮąĄ čāčćąĖčéčŗą▓ą░ąĄčéčüčÅ.
ąóą░ą▒ą╗ąĖčåą░ 4-2: ąĘą░čéčĆą░čéčŗ ą┐čĆąŠčåąĄčüčüąŠčĆąĮąŠą│ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ąĮą░ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ FIR-čäąĖą╗čīčéčĆą░ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░.
ąśąĮčüčéčĆčāą║čåąĖą╣ (čäąĖą╗čīčéčĆą░čåąĖčÅ + ą┤ąŠą┐. čĆą░čüčģąŠą┤čŗ)
|
ą”ąĖą║ą╗ąŠą▓ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ (čäąĖą╗čīčéčĆą░čåąĖčÅ + ą┤ąŠą┐. čĆą░čüčģąŠą┤čŗ) |
ąŁčäč乥ą║čéąĖą▓ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░ (ą║ąŠą╗ąĖč湥čüčéą▓ąŠ čåąĖą║ą╗ąŠą▓ čäąĖą╗čīčéčĆą░ ą▓ ą┐ąĄčĆąĄčüč湥č鹥 ąĮą░ ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░)
|
| 50+10 |
76+10 |
38 |
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ą┐ąŠčĆčÅą┤ą║ą░ čäąĖą╗čīčéčĆą░ ą╝ąŠąČąĄčé ą┐čĆąĖąĮčāą┤ąĖčéčī ą║ ąĖąĘą╝ąĄąĮąĄąĮąĖčÄ čĆą░ąĘą╝ąĄčĆą░ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, čćč鹊 ąĖąĘą╝ąĄąĮąĖčé ą║ąŠą╗ąĖč湥čüčéą▓ąŠ ąĘą░čéčĆą░čćąĖą▓ą░ąĄą╝čŗčģ ąĖąĮčüčéčĆčāą║čåąĖą╣/čåąĖą║ą╗ąŠą▓ ą┐čĆąŠčåąĄčüčüąŠčĆą░. ąŁčäč乥ą║čéąĖą▓ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░ ą▓ ą┐ąĄčĆąĄčüč湥č鹥 ąĮą░ ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ (ą┐ąŠčüą╗ąĄą┤ąĮąĖą╣ čüč鹊ą╗ą▒ąĄčå čéą░ą▒ą╗ąĖčåčŗ) čéą░ą║ąČąĄ ą┐ąŠą╝ąĄąĮčÅąĄčéčüčÅ.
4.2 IIR-čäąĖą╗čīčéčĆ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
ąöą╗čÅ čŹč鹊ą╣ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ą┐čĆąĖą╝ąĄąĮąĄąĮ ą┐ąŠą╗ąŠčüąŠą▓ąŠą╣ (Band Pass, BP) IIR-čäąĖą╗čīčéčĆ ąæą░čéč鹥čĆą▓ąŠčĆčéą░. ą¤ą░čĆą░ą╝ąĄčéčĆčŗ čäąĖą╗čīčéčĆą░ ą┐ąŠą║ą░ąĘą░ąĮčŗ ą▓ ąóą░ą▒ą╗ąĖčåąĄ 4-3, ąÉą¦ąź ąĮą░ ąĀąĖčüčāąĮą║ąĄ 4-3.
ąóą░ą▒ą╗ąĖčåą░ 4-4: ą┐ą░čĆą░ą╝ąĄčéčĆčŗ IIR-čäąĖą╗čīčéčĆą░ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░
| ą¤ąŠčĆčÅą┤ąŠą║ |
ąĪčĆąĄąĘ
|
ąÜąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ (b0,b1,b2;a0,a1,a2)
|
ą£ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ
|
ąĪą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĮčŗąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ(b0,b1,b2;a0,a1,a2) |
| 2 |
0.45 -
0.55 |
0.1367, 0.0000, -0.1367;
1.0000, 0.0000, 0.7265 |
211 |
280, 0, -280;
2048, 0, 1488 |
ą¤ąŠčüą║ąŠą╗čīą║čā ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé a0 ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčé ą╝ąĮąŠąČąĖč鹥ą╗čī ą┤ą╗čÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ ą▓čŗčģąŠą┤ą░ čäąĖą╗čīčéčĆą░, ąŠąĮ ąĮąĄ ąĘą░ą┤ą░ąĮ ą▓ ą║ąŠą┤ąĄ ąĮą░ čÅąĘčŗą║ąĄ C, ą░ ą┐čĆąŠčüč鹊 ąĘą░ą┤ą░ąĮ ą▓ ą║ąŠą┤ąĄ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░ ą┤ą╗čÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ.
ąĀąĖčüčāąĮąŠą║ 4-3: ąÉą¦ąź IIR-čäąĖą╗čīčéčĆą░ 2-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░

ąĪčéčĆčāą║čéčāčĆą░ čüąŠą┤ąĄčƹȹĖčé ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ ąĖ čāąĘą╗čŗ čäąĖą╗čīčéčĆą░. ążąĖą╗čīčéčĆ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą┐čĆąŠąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮ ą┐ąĄčĆąĄą┤ č鹥ą╝, ą║ą░ą║ ą▒čāą┤ąĄčé ą▓čŗąĘą▓ą░ąĮą░ čäčāąĮą║čåąĖčÅ čäąĖą╗čīčéčĆą░. ąĪčéčĆčāą║čéčāčĆą░ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮą░ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝:
struct IIR_filter
{
int filterNodesX[FILTER_ORDER]; //čāąĘą╗čŗ čäąĖą╗čīčéčĆą░, čéčāčé čüąŠčģčĆą░ąĮčÅčÄčéčüčÅ ą▓čģąŠą┤ąĮčŗąĄ ą▓čŗą▒ąŠčĆą║ąĖ x(n-k)
int filterNodesY[FILTER_ORDER]; //čāąĘą╗čŗ čäąĖą╗čīčéčĆą░, čéčāčé čüąŠčģčĆą░ąĮčÅčÄčéčüčÅ ą▓čŗčģąŠą┤ąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ y(n-k)
int filterCoefficientsB[FILTER_ORDER+1]; //feedforward ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ (bj)
int filterCoefficientsA[FILTER_ORDER]; //feedback ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ (ai)
} filter04_06 = {0,0,0,0, B0, B1, B2, A1, A2}; //ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÅ čäąĖą╗čīčéčĆą░
ą£ą░čüčüąĖą▓čŗ filterNodesX ąĖ filterNodesY ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ ą║ą░ą║ ą▒čāč乥čĆčŗ FIFO, čüąŠčģčĆą░ąĮčÅčÄčēąĖąĄ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ ą▓čģąŠą┤ąĮčŗąĄ ąĖ ą▓čŗčģąŠą┤ąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ čüąĖą│ąĮą░ą╗ą░ čäąĖą╗čīčéčĆą░. ą£ą░čüčüąĖą▓čŗ filterCoefficientsB ąĖ filterCoefficientsA ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ ą┤ą╗čÅ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ feed-forward ąĖ feedback. ą¤ąŠčüą╗ąĄ ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ą▓čŗąĘą▓ą░ąĮą░ čäčāąĮą║čåąĖčÅ čäąĖą╗čīčéčĆą░. ążčāąĮą║čåąĖčÅ čäąĖą╗čīčéčĆą░ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮą░ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝:
int IIR2(struct IIR_filter *myFilter, int newSample);
ąĪąĮą░čćą░ą╗ą░ čäčāąĮą║čåąĖčÅ ą║ąŠą┐ąĖčĆčāąĄčé čāą║ą░ąĘą░č鹥ą╗čī ąĮą░ čüčéčĆčāą║čéčāčĆčā čäąĖą╗čīčéčĆą░ ą▓ Z-čĆąĄą│ąĖčüčéčĆ, ą┐ąŠčüą║ąŠą╗čīą║čā ąŠąĮ ą╝ąŠąČąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ąĮąĄą┐čĆčÅą╝ąŠą╣ (indirect) ą░ą┤čĆąĄčüą░čåąĖąĖ ą┤ą░ąĮąĮčŗčģ, ąĮą░ą┐čĆąĖą╝ąĄčĆ ą┤ą╗čÅ ąŠą┐ąĄčĆą░čåąĖą╣ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čāą║ą░ąĘą░č鹥ą╗čÅ. ąŚą░č鹥ą╝ ąŠčüąĮąŠą▓ąĮąŠą╣ ą░ą╗ą│ąŠčĆąĖčéą╝ ą│ąŠč鹊ą▓ ą║ ąĘą░ą┐čāčüą║čā. ąÆčŗą▒ąŠčĆą║ąĖ ą▓čģąŠą┤ą░ ąĖ ą┤ą░ąĮąĮčŗąĄ ą▓čŗčģąŠą┤ą░ (čāąĘą╗čŗ čäąĖą╗čīčéčĆą░) ąĘą░ą│čĆčāąČą░čÄčéčüčÅ ąĖ čāą╝ąĮąŠąČą░čÄčéčüčÅ čü čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĖą╝ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ą╝ąĖ. ąĀąĄąĘčāą╗čīčéą░čéčŗ ą┤ąŠą▒ą░ą▓ą╗čÅčÄčéčüčÅ ą▓ 24-ą▒ąĖčéąĮčŗą╣ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆ. ąÜąŠą│ą┤ą░ ą▓čüąĄ ą▓čŗą▒ąŠčĆą║ąĖ ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čāą╝ąĮąŠąČąĄąĮčŗ ąĖ čüąŠčģčĆą░ąĮąĄąĮčŗ (multiplied-and-accumulated, ąŠą┐ąĄčĆą░čåąĖčÅ MAC), čāąĘą╗čŗ čäąĖą╗čīčéčĆą░ ą▓ FIFO-ą▒čāč乥čĆąĄ ąŠą▒ąĮąŠą▓ą╗ąĄąĮčŗ, čĆąĄąĘčāą╗čīčéą░čé ą╝ą░čüčłčéą░ą▒ąĖčĆčāąĄčéčüčÅ ą▓ąĮąĖąĘ ąĖ ą▓ąŠąĘą▓čĆą░čēą░ąĄčéčüčÅ. ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 čĆąĄąĘčāą╗čīčéą░čé ą▓ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆąĄ ą╝ą░čüčłčéą░ą▒ąĖčĆčāąĄčéčüčÅ ą▓ąĮąĖąĘ ą┐ąĄčĆąĄą┤ čüąŠčģčĆą░ąĮąĄąĮąĖąĄą╝ ąĄą│ąŠ ą▓ čā[n-1] čÅč湥ą╣ą║ąĄ ą▒čāč乥čĆą░ FIFO. ą¤čĆąŠčåąĄčüčü ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ą╝ąŠąČąĮąŠ čāą▓ąĖą┤ąĄčéčī ąĮą░ ąĀąĖčüčāąĮą║ąĄ 4-4, ą║ąŠč鹊čĆčŗą╣ ąŠą┐ąĖčüčŗą▓ą░ąĄčé ą┤ąĄą╣čüčéą▓ąĖčÅ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░ IIR.
ąĀąĖčüčāąĮąŠą║ 4-4: Generic (čéčĆą░ą┤ąĖčåąĖąŠąĮąĮčŗą╣) ą░ą╗ą│ąŠčĆąĖčéą╝ IIR-čäąĖą╗čīčéčĆą░

ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ąĮąĄčüą╝ąŠčéčĆčÅ ąĮą░ č鹊, čćč鹊 ą┤ąĖą░ą│čĆą░ą╝ą╝ą░ ąĮą░ ąĀąĖčüčāąĮą║ąĄ 4-4 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą░ą╗ą│ąŠčĆąĖčéą╝, čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąĮčŗą╣ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čåąĖą║ą╗ąŠą▓, ąĮą░ čüą░ą╝ąŠą╝ ą┤ąĄą╗ąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮ ą╗ąĖąĮąĄą╣ąĮčŗą╝ ą║ąŠą┤ąŠą╝ (ą┤ą╗čÅ čāą▓ąĄą╗ąĖč湥ąĮąĖčÅ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ). ą”ąĖą║ą╗ ąĮą░ ą┤ąĖą░ą│čĆą░ą╝ą╝ąĄ ą┐čĆąŠčüč鹊 ą┐čĆąĖą╝ąĄąĮąĄąĮ ą┤ą╗čÅ čāą╗čāčćčłąĄąĮąĖčÅ čćąĖčéą░ąĄą╝ąŠčüčéąĖ ą░ą╗ą│ąŠčĆąĖčéą╝ą░.
4.2.1 ąĪą║ąŠčĆąŠčüčéčī čĆą░ą▒ąŠčéčŗ IIR-čäąĖą╗čīčéčĆą░
ąóą░ą▒ą╗ąĖčåą░ 4-4 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖąĄ IIR-čäąĖą╗čīčéčĆą░ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░. ąŚąĮą░č湥ąĮąĖąĄ čüč湥čéčćąĖą║ą░ ą▓ čéą░ą▒ą╗ąĖčåąĄ ą┐ąŠą║ą░ąĘčŗą▓ą░čÄčé ąĘą░čéčĆą░čéčŗ ą▓čĆąĄą╝ąĄąĮąĖ (ą▓ čåąĖą║ą╗ą░čģ čÅą┤čĆą░ AVR) ąĮą░ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ čäąĖą╗čīčéčĆą░ (ąŠą┐ąĄčĆą░čåąĖąĖ MUL ąĖ MAC, ąŠą▒ąĮąŠą▓ą╗ąĄąĮąĖąĄ čāąĘą╗ąŠą▓), ą░ čéą░ą║ąČąĄ ąĮą░ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčāčÄ ąŠą▒čĆą░ą▒ąŠčéą║čā ą┐čĆąĖ ąĘą░ą▓ąĄčĆčłąĄąĮąĖąĖ čäčāąĮą║čåąĖąĖ (ą▓ą║ą╗čÄčćą░čÅ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĄ ą▓ąĮąĖąĘ). ąÆčĆąĄą╝čÅ, ąĘą░čéčĆą░č湥ąĮąĮąŠąĄ ąĮą░ ą▓čŗąĘąŠą▓čŗ (call) ąĖ ą▓ąŠąĘą▓čĆą░čé ąĖąĘ čäčāąĮą║čåąĖąĖ (return), ą▓ čéą░ą▒ą╗ąĖčåąĄ ąĮąĄ čāčćąĖčéčŗą▓ą░ąĄčéčüčÅ.
ąóą░ą▒ą╗ąĖčåą░ 4-4: ąĘą░čéčĆą░čéčŗ ą┐čĆąŠčåąĄčüčüąŠčĆąĮąŠą│ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ąĮą░ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ IIR-čäąĖą╗čīčéčĆą░ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░.
ąśąĮčüčéčĆčāą║čåąĖą╣ (čäąĖą╗čīčéčĆą░čåąĖčÅ + ą┤ąŠą┐. čĆą░čüčģąŠą┤čŗ)
|
ą”ąĖą║ą╗ąŠą▓ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ (čäąĖą╗čīčéčĆą░čåąĖčÅ + ą┤ąŠą┐. čĆą░čüčģąŠą┤čŗ) |
ąŁčäč乥ą║čéąĖą▓ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░ (ą║ąŠą╗ąĖč湥čüčéą▓ąŠ čåąĖą║ą╗ąŠą▓ čäąĖą╗čīčéčĆą░ ą▓ ą┐ąĄčĆąĄčüč湥č鹥 ąĮą░ ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░)
|
| 86+8 |
132+8 |
66 |
ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ą┐ąŠčĆčÅą┤ą║ą░ čäąĖą╗čīčéčĆą░ ą╝ąŠąČąĄčé ą┐čĆąĖąĮčāą┤ąĖčéčī ą║ ąĖąĘą╝ąĄąĮąĄąĮąĖčÄ čĆą░ąĘą╝ąĄčĆą░ ą░ą║ą║čāą╝čāą╗čÅč鹊čĆą░, čćč鹊 ąĖąĘą╝ąĄąĮąĖčé ą║ąŠą╗ąĖč湥čüčéą▓ąŠ ąĘą░čéčĆą░čćąĖą▓ą░ąĄą╝čŗčģ ąĖąĮčüčéčĆčāą║čåąĖą╣/čåąĖą║ą╗ąŠą▓ ą┐čĆąŠčåąĄčüčüąŠčĆą░. ąŁčäč乥ą║čéąĖą▓ąĮąŠčüčéčī čäąĖą╗čīčéčĆą░ ą▓ ą┐ąĄčĆąĄčüč湥č鹥 ąĮą░ ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ (ą┐ąŠčüą╗ąĄą┤ąĮąĖą╣ čüč鹊ą╗ą▒ąĄčå čéą░ą▒ą╗ąĖčåčŗ) čéą░ą║ąČąĄ ą┐ąŠą╝ąĄąĮčÅąĄčéčüčÅ.
[5. ą×ą┐čéąĖą╝ąĖąĘą░čåąĖčÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆą░]
ążąĖą╗čīčéčĆčŗ, čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąĮčŗąĄ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ ą▓ ą║ą░č湥čüčéą▓ąĄ ą┐čĆąĖą╝ąĄčĆą░, čüą┤ąĄą╗ą░ąĮčŗ čŹčäč乥ą║čéąĖą▓ąĮąŠ, ąŠą┤ąĮą░ą║ąŠ ąĄčüčéčī ąĄčēąĄ čĆąĄąĘąĄčĆą▓čŗ ą┤ą╗čÅ čāą▓ąĄą╗ąĖč湥ąĮąĖčÅ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ. ą¤čĆąĖčćąĖąĮą░ ą▓ č鹊ą╝, čćč鹊 čäąĖą╗čīčéčĆčŗ ą▓ ą┐čĆąĖą╝ąĄčĆą░čģ čāąĮąĖą▓ąĄčĆčüą░ą╗čīąĮčŗ, ą░ ą║ąŠąĮą║čĆąĄčéąĮą░čÅ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ čāąĘą║ąŠčüą┐ąĄčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮąĮčŗčģ čäąĖą╗čīčéčĆąŠą▓ ą╝ąŠąČąĄčé ą▒čŗčéčī čüą┤ąĄą╗ą░ąĮą░ ą▒ąŠą╗ąĄąĄ ąŠą┐čéąĖą╝ą░ą╗čīąĮąŠ. ąöą░ą╗ąĄąĄ ąŠą┐ąĖčüą░ąĮčŗ ą┐čāčéąĖ ą┤ą╗čÅ ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĖ čäąĖą╗čīčéčĆąŠą▓ ą┐ąŠ čĆą░ąĘą╝ąĄčĆčā ą║ąŠą┤ą░ ąĖ/ąĖą╗ąĖ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÄ.
5.1 ąŻą╝ąĄąĮčīčłąĄąĮąĖąĄ ąŠą▒čŖąĄą╝ą░ ą║ąŠą┤ą░ ąĖ čāą▓ąĄą╗ąĖč湥ąĮąĖąĄ ą┐čĆąŠą┐čāčüą║ąĮąŠą╣ čüą┐ąŠčüąŠą▒ąĮąŠčüčéąĖ
ą×ą┤ąĖąĮ ąĖąĘ ą┐čāč鹥ą╣ ąŠą┤ąĮąŠą▓čĆąĄą╝ąĄąĮąĮąŠą│ąŠ čāą╝ąĄąĮčīčłąĄąĮąĖčÅ ąŠą▒čŖąĄą╝ą░ ą║ąŠą┤ą░ ąĖ čāą▓ąĄą╗ąĖč湥ąĮąĖčÅ ą┐čĆąŠą┐čāčüą║ąĮąŠą╣ čüą┐ąŠčüąŠą▒ąĮąŠčüčéąĖ - ąĮčāąČąĮąŠ čāą▒ąĄą┤ąĖčéčīčüčÅ ą▓ č鹊ą╝, čćč鹊 ą▓čŗą┐ąŠą╗ąĮčÅčÄčéčüčÅ č鹊ą╗čīą║ąŠ ąĮąĄąŠą▒čģąŠą┤ąĖą╝čŗąĄ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ. ąÉčüčüąĄą╝ą▒ą╗ąĄčĆąĮčŗą╣ ą║ąŠą┤ ą┤ą╗čÅ čäąĖą╗čīčéčĆąŠą▓, čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąĮčŗą╣ ą▓ ą┐čĆąĖą╝ąĄčĆą░čģ ąĖąĘ čüčéą░čéčīąĖ, čüą┤ąĄą╗ą░ąĮ čéą░ą║, čćč鹊 ąŠąĮ ą▒čāą┤ąĄčé čĆą░ą▒ąŠčéą░čéčī čü ą╗čÄą▒čŗą╝ ąĮą░ą▒ąŠčĆąŠą╝ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čäąĖą╗čīčéčĆą░. ą×ą┤ąĮą░ą║ąŠ IIR-čäąĖą╗čīčéčĆ ą▓č鹊čĆąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░ ąĖą╝ąĄąĄčé ą┤ą▓ą░ ąĮčāą╗ąĄą▓čŗčģ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░. ąŻą╝ąĮąŠąČąĄąĮąĖąĄ ąĖ ą┐ąŠčüą╗ąĄą┤čāčÄčēąĄąĄ ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄ čü ąĮčāą╗ąĄą▓čŗą╝ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ą╝ąĖ ą╝ąŠąČąĄčé ą▒čŗčéčī, ą║ąŠąĮąĄčćąĮąŠ, ąŠą┐čāčēąĄąĮąŠ - čćč鹊 ąĮąĖą║ą░ą║ ąĮąĄ ą┐ąŠą▓ą╗ąĖčÅąĄčé ąĮą░ čĆą░ą▒ąŠčéčā čäąĖą╗čīčéčĆą░, ąĮąŠ čāą▓ąĄą╗ąĖčćąĖčé ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖąĄ ąĖ čāą╝ąĄąĮčīčłąĖčé čĆą░ąĘą╝ąĄčĆ ą║ąŠą┤ą░.
5.2 ąŻą╝ąĄąĮčīčłąĄąĮąĖąĄ čĆą░ąĘą╝ąĄčĆą░ ą║ąŠą┤ą░
ąŻą╝ąĄąĮčīčłąĄąĮąĖąĄ čĆą░ąĘą╝ąĄčĆą░ ą║ąŠą┤ą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ą┤ąŠčüčéąĖą│ąĮčāč鹊 ą┐čāč鹥ą╝ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ MAC ą║ą░ą║ ą▓čŗąĘąŠą▓ą░ čäčāąĮą║čåąĖąĖ, ą▓ą╝ąĄčüč鹊 čŹč鹊ą╣ ąŠą┐ąĄčĆą░čåąĖąĖ, ą▓čŗą┐ąŠą╗ąĮąĄąĮąĮąŠą╣ ą║ą░ą║ ą╝ą░ą║čĆąŠčü. ą×ą┤ąĮą░ą║ąŠ čŹč鹊 čāą┤ą░čĆąĖčé ą┐čĆąŠ ą┐čĆąŠą┐čāčüą║ąĮąŠą╣ čüą┐ąŠčüąŠą▒ąĮąŠčüčéąĖ, čéą░ą║ ą║ą░ą║ ąĮą░ ą║ą░ąČą┤čŗą╣ ą▓čŗąĘąŠą▓ ąĖ ą▓ąŠąĘą▓čĆą░čé ąĖąĘ čäčāąĮą║čåąĖąĖ čéčĆą░čéčÅčéčüčÅ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗąĄ čåąĖą║ą╗čŗ ą┐čĆąŠčåąĄčüčüąŠčĆą░.
ąöčĆčāą│ąŠą╣ ą┐čāčéčī čāą╝ąĄąĮčīčłąĄąĮąĖčÅ ąŠą▒čŖąĄą╝ą░ ą║ąŠą┤ą░ - čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ čäąĖą╗čīčéčĆąŠą▓ ą▓čŗčüąŠą║ąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░ čü ą┐ąŠą╝ąŠčēčīčÄ ą║ą░čüą║ą░ą┤ąĖčĆąŠą▓ą░ąĮąĖčÅ čäąĖą╗čīčéčĆąŠą▓ ą╝ąĄąĮčīčłąĄą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░, ą║ą░ą║ ą┐čĆąŠą┤ąĄą╝ąŠąĮčüčéčĆąĖčĆąŠą▓ą░ąĮąŠ ąĮą░ FIR-čäąĖą╗čīčéčĆąĄ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░. ąźąŠčéčÅ, ą║ą░ą║ ąŠčéą╝ąĄčćą░ą╗ąŠčüčī čĆą░ąĮąĄąĄ, čŹč鹊 čāą╝ąĄąĮčīčłąĖčé č鹊čćąĮąŠčüčéčī čäąĖą╗čīčéčĆą░ ąĖąĘ-ąĘą░ ą┐čĆąŠą╝ąĄąČčāč鹊čćąĮąŠą│ąŠ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓ąĮąĖąĘ ąĮą░ ą║ą░ąČą┤ąŠą╝ ą║ą░čüą║ą░ą┤ąĄ. ąÜčĆąŠą╝ąĄ č鹊ą│ąŠ, ąĮąĄ ą┐ąŠą╗čāčćąĖčéčüčÅ ą▓čŗą┐ąŠą╗ąĮąĖčéčī ąŠą┐čéąĖą╝ąĖąĘą░čåąĖčÄ ą┐čāč鹥ą╝ ą┐čĆąŠą┐čāčüą║ą░ MAC-ąŠą┐ąĄčĆą░čåąĖą╣ ąĮą░ ąĮčāą╗ąĄą▓čŗčģ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░čģ, čéą░ą║ ą║ą░ą║ čŹč鹊 ą▓ąŠąĘą╝ąŠąČąĮąŠ ąĮąĄ ą┤ą╗čÅ ą▓čüąĄčģ čĆąĄą░ą╗ąĖąĘą░čåąĖą╣ čäąĖą╗čīčéčĆą░.
5.3 ąŻą╝ąĄąĮčīčłąĄąĮąĖąĄ čĆą░ąĘą╝ąĄčĆą░ ąĖčüą┐ąŠą╗čīąĘčāąĄą╝ąŠą╣ ą┐ą░ą╝čÅčéąĖ (RAM)
ąÜąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čäąĖą╗čīčéčĆą░ ą▓ ąŠą▒ąŠąĖčģ ą┐čĆąĖą╝ąĄčĆą░čģ čĆąĄą░ą╗ąĖąĘą░čåąĖą╣ čĆą░ąĘą╝ąĄčēą░čÄčéčüčÅ ą▓ SRAM. ą¤čĆąŠčüč鹊ą╣ ą┐čāčéčī čāą╝ąĄąĮčīčłąĄąĮąĖčÅ ą┐ą░ą╝čÅčéąĖ - čĆą░ąĘą╝ąĄčēąĄąĮąĖąĄ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ ą▓ FLASH ąĖ ą▓čŗą▒ąŠčĆą║ą░ ąĖčģ ą┐ąŠ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠčüčéąĖ. ąŁč鹊 ą┐ąŠč鹥ąĮčåąĖą░ą╗čīąĮąŠ ą┐ąŠčćčéąĖ ąĮą░ą┐ąŠą╗ąŠą▓ąĖąĮčā čāą╝ąĄąĮčīčłąĖčé čĆą░čüčģąŠą┤ ą┐ą░ą╝čÅčéąĖ ą┤ą╗čÅ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ čäąĖą╗čīčéčĆą░, ą┐ąŠčüą║ąŠą╗čīą║čā ąĮą░ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ čéčĆą░čéąĖčéčüčÅ ą┐ąŠčćčéąĖ čüč鹊ą╗čīą║ąŠ ąČąĄ ą┐ą░ą╝čÅčéąĖ, ą║ą░ą║ ąĖ ąĮą░ čāąĘą╗čŗ (ą┐čĆąĄą┤čŗą┤čāčēąĖąĄ čüąŠčüč鹊čÅąĮąĖčÅ ą▓čģąŠą┤ą░ ąĖ ą▓čŗčģąŠą┤ą░) čäąĖą╗čīčéčĆą░.
[ąŚą░č湥ą╝ ą▓čüąĄ čŹč鹊? (ą× č湥ą╝ ą▓ąŠąŠą▒čēąĄ čéčāčé ą│ąŠą▓ąŠčĆąĖčéčüčÅ?..)]
ąĢčüą╗ąĖ ąÆčŗ ą┤ąŠčćąĖčéą░ą╗ąĖ čüčéą░čéčīčÄ ą┤ąŠ ą║ąŠąĮčåą░ (ąĮą░ą┐ąŠą╝ąĮčÄ, čćč鹊 čŹč鹊 ą░ą┐ąĮąŠčāčé Atmel AVR223), č鹊 ąĘąĮą░čćąĖčé, čćč鹊 ąÆą░čü ą▓ ąĮąĄą║ąŠč鹊čĆąŠą╣ čüč鹥ą┐ąĄąĮąĖ ąĖąĮč鹥čĆąĄčüčāąĄčé čåąĖčäčĆąŠą▓ą░čÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░ čüąĖą│ąĮą░ą╗ąŠą▓ (ą”ą×ąĪ). ąĢčüą╗ąĖ ąČąĄ ąÆčŗ ą┐ąŠčćčéąĖ ą▓čüąĄ ą┐ąŠąĮčÅą╗ąĖ ą▓ čŹč鹊ą╣ čüčéą░čéčīąĄ (čÅ, ąĮą░ą┐čĆąĖą╝ąĄčĆ, ąĮąĄ ą┐ąŠąĮčÅą╗ č鹊ą╗čīą║ąŠ Z-ą┤ąŠą╝ąĄąĮ, Z-ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ ąĖ ą▓čüąĄ, čćč鹊 čü čŹčéąĖą╝ čüą▓čÅąĘą░ąĮąŠ), č鹊 ąÆčŗ čĆą░ąĮčīčłąĄ čāąČąĄ ąĖąĮč鹥čĆąĄčüąŠą▓ą░ą╗ąĖčüčī ą”ą×ąĪ, ąĖ ąĮąĄą╝ąĮąŠą│ąŠ ąĘąĮą░ą║ąŠą╝čŗ čü ąŠą▒čēąĖą╝ąĖ ą┐čĆąĖąĮčåąĖą┐ą░ą╝ąĖ, ąĮąŠ ąĮąĄ ą▓ąĖą┤ąĄą╗ąĖ čĆąĄą░ą╗čīąĮąŠą│ąŠ čüą┐ąŠčüąŠą▒ą░ ą▓čŗą┐ąŠą╗ąĮąĖčéčī ą║ą░ą║čāčÄ-ąĮąĖą▒čāą┤čī (ą┤ą░ąČąĄ čüą░ą╝čāčÄ ą┐čĆąŠčüčéčāčÄ) ąĘą░ą┤ą░čćčā ą”ą×ąĪ. ą¤ąŠąĘą┤čĆą░ą▓ą╗čÅčÄ! ąóąĄą┐ąĄčĆčī čā ąÆą░čü ą▓ čĆčāą║ą░čģ ą│ąŠč鹊ą▓čŗą╣ ąĖąĮčüčéčĆčāą╝ąĄąĮčé, čģąŠčĆąŠčłą░čÅ č鹊čćą║ą░ ą┤ą╗čÅ čüčéą░čĆčéą░ čüąŠąĘą┤ą░ąĮąĖčÅ čüą▓ąŠąĖčģ čüąŠą▒čüčéą▓ąĄąĮąĮčŗčģ ą┐čĆąŠą│čĆą░ą╝ą╝. ą¦ąĄą╝ ą╝ąĮąĄ ą▒ąŠą╗čīčłąĄ ą▓čüąĄą│ąŠ ą┐ąŠąĮčĆą░ą▓ąĖą╗čüčÅ ą░ą┐ąĮąŠčāčé AVR223 - ą┤ą░ąĄčéčüčÅ ą▓ čüąČą░č鹊ą╝ ą▓ąĖą┤ąĄ ąĖą╝ąĄąĮąĮąŠ č鹊, čćč鹊 ąĮčāąČąĮąŠ ą┤ą╗čÅ ąĮą░čćą░ą╗ą░ - ą┐čĆąŠčüč鹊 ą▒ąĄčĆąĖ ąĖ ą┤ąĄą╗ą░ą╣ (ą┐čĆąĖč湥ą╝ ą╝ąŠąČąĮąŠ ą┤ąĄą╗ą░čéčī ąĮąĄ č鹊ą╗čīą║ąŠ ąĮą░ AVR, ąĄčüą╗ąĖ ąŠčüąĮąŠą▓ąĮąŠą╣ ą┐čĆąĖąĮčåąĖą┐ ą┐ąŠąĮčÅč鹥ąĮ).
ąÆ ąĘą░ą║ą╗čÄč湥ąĮąĖąĄ čģąŠčćčā ą┐čĆąĖą▓ąĄčüčéąĖ ąĮąĄčüą║ąŠą╗čīą║ąŠ čüąŠąŠą▒čĆą░ąČąĄąĮąĖą╣ ą┐ąŠ ą┐ąŠą▓ąŠą┤čā ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗ąĄąĮąĮąŠą╣ ą▓ ą░ą┐ąĮąŠčāč鹥 AVR223 ąĖąĮč乊čĆą╝ą░čåąĖąĖ - ą║ą░ą║ ąĮą░ ąŠčüąĮąŠą▓ąĄ ąĮąĄčæ čüą┤ąĄą╗ą░čéčī čüą▓ąŠą╣ čüąŠą▒čüčéą▓ąĄąĮąĮčŗą╣ DSP-čäąĖą╗čīčéčĆ. ąÆčüąĄ ąĮą░ ą┐čĆąĖą╝ąĄčĆąĄ č鹊ą╣ ąČąĄ ą┐ą╗ą░čéč乊čĆą╝čŗ AVR, ą║ąŠč鹊čĆą░čÅ ąĖ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄčéčüčÅ ą▓ čüčéą░čéčīąĄ.
1. ąĪąĮą░čćą░ą╗ą░ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ą┐ąŠąĮčÅčéčī - č湥ą│ąŠ ą╝čŗ ą╝ąŠąČąĄą╝, ąĖ č湥ą│ąŠ ąĮąĄ ą╝ąŠąČąĄą╝. ąóąŠ ąĄčüčéčī ą║ą░ą║čāčÄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčāčÄ ą┐ąŠą╗ąŠčüčā čćą░čüč鹊čé ą╝čŗ čüą╝ąŠąČąĄą╝ ąŠą▒čĆą░ą▒ąŠčéą░čéčī, ąĖ ą║ą░ą║ąŠą╣ ą┐ąŠčĆčÅą┤ąŠą║ čäąĖą╗čīčéčĆą░ ą┐čĆąĖ čŹč鹊ą╝ ą╝ąŠąČąĮąŠ ą┐čĆąĖą╝ąĄąĮąĖčéčī (ą┐čĆąĖ č鹊ą╣ ąČąĄ čüą░ą╝ąŠą╣ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ čüąĖą│ąĮą░ą╗ą░ 10 ą▒ąĖčé, čćč鹊 ą┐čĆąĖą╝ąĄąĮąĄąĮą░ ą▓ ą┐čĆąĖą╝ąĄčĆą░čģ). ą¤ąŠąĮčÅčéąĮąŠ, čćč鹊 č湥ą╝ ą▓čŗčłąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ čĆą░ą▒ąŠčćą░čÅ čćą░čüč鹊čéą░, ą║ąŠč鹊čĆčāčÄ ą╝čŗ ą╝ąŠąČąĄą╝ ą┐čĆąŠą┐čāčüčéąĖčéčī č湥čĆąĄąĘ čäąĖą╗čīčéčĆ, č鹥ą╝ čäąĖą╗čīčéčĆ ą║ą░č湥čüčéą▓ąĄąĮąĮąĄąĄ, ąĖ č鹥ą╝ ą┐čĆąŠčēąĄ ą┤ąĄą╗ą░čéčī ą┐čĆąĄą┤ą▓ą░čĆąĖč鹥ą╗čīąĮčāčÄ ą░ąĮą░ą╗ąŠą│ąŠą▓čāčÄ čäąĖą╗čīčéčĆą░čåąĖčÄ (ąŠą▒ čŹč鹊ą╝ ą┐ąŠąĘąČąĄ). ą×čé ą┐ąŠčĆčÅą┤ą║ą░ čäąĖą╗čīčéčĆą░ ąĘą░ą▓ąĖčüąĖčé ą║čĆčāčéąĖąĘąĮą░ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ čäąĖą╗čīčéčĆą░, čé. ąĄ. ąĮą░čüą║ąŠą╗čīą║ąŠ čģąŠčĆąŠčłąŠ čäąĖą╗čīčéčĆ ąŠčüą╗ą░ą▒ą╗čÅąĄčé ąĮąĄąĮčāąČąĮčŗą╣ čüąĖą│ąĮą░ą╗ (ą┤ą╗čÅ čāą┐čĆąŠčēąĄąĮąĖčÅ ą┐ąŠą║ą░ ąĮąĄ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝ ą┤čĆčāą│ąĖąĄ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ čäąĖą╗čīčéčĆą░ čéąĖą┐ą░ ą│čĆčāą┐ą┐ąŠą▓ąŠą╣ ąĘą░ą┤ąĄčƹȹ║ąĖ, čäą░ąĘąŠčćą░čüč鹊čéąĮąŠą╣ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ ąĖ čé. ą┐.). ąśčüčģąŠą┤čÅ ąĖąĘ ą┐čĆąĄą┤ą┐ąŠą╗ąŠąČąĄąĮąĖčÅ, čćč鹊 ą║ą▓ą░čĆčå čā ąĮą░čü ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą▓ąŠąĘą╝ąŠąČąĮčŗą╣ ą┤ą╗čÅ AVR 20 ą£ąōčå, ą┐ąŠ čéą░ą▒ą╗ąĖčåą░ą╝ 4-2 ąĖ 4-4 ą╝ąŠąČąĮąŠ ą┐ąŠą┤čüčćąĖčéą░čéčī ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą▓ąŠąĘą╝ąŠąČąĮčāčÄ čćą░čüč鹊čéčā ą▓čŗą▒ąŠčĆąŠą║ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░, ą║ąŠč鹊čĆčāčÄ ą╝čŗ čāčüą┐ąĄąĄą╝ ąŠą▒čĆą░ą▒ąŠčéą░čéčī. ąØą░ą┐čĆąĖą╝ąĄčĆ, čā ąĮą░čü FIR-čäąĖą╗čīčéčĆ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░ (čé. ąĄ. ą┤ą▓ą░ FIR-čäąĖą╗čīčéčĆą░ 2-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░, čüąŠąĄą┤ąĖąĮąĄąĮąĮčŗąĄ ą▓ čåąĄą┐ąŠčćą║čā - ąĖą╝ąĄąĮąĮąŠ čéą░ą║, ą║ą░ą║ ąŠą┐ąĖčüčŗą▓ą░ąĄčéčüčÅ ą▓ čüčéą░čéčīąĄ). ąóąŠą│ą┤ą░ ą┐ąŠą╗čāčćą░ąĄčéčüčÅ, čćč鹊 ą┐ąŠą╗ąĮčŗą╣ ą┐čĆąŠčģąŠą┤ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ čäąĖą╗čīčéčĆą░ ąĘą░ą╣ą╝ąĄčé (ą┐ąŠ ąóą░ą▒ą╗ąĖčåąĄ 4-2), čü čāč湥č鹊ą╝ ą▓čŗąĘąŠą▓ą░ ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ FIR
2 + 76 + 10 + 2 = 90 čåąĖą║ą╗ąŠą▓.
ąĢčüą╗ąĖ čāč湥čüčéčī ąĄčēąĄ ą▓čĆąĄą╝čÅ ąĮą░ čćč鹥ąĮąĖąĄ čĆąĄąĘčāą╗čīčéą░č鹊ą▓ čü ąÉą”ą¤ ąĖ ą▓čĆąĄą╝čÅ ąĮą░ ąŠą▒čĆą░ą▒ąŠčéą║čā ą┐čĆąĄčĆčŗą▓ą░ąĮąĖčÅ (ą▓ čĆąĄą░ą╗čīąĮąŠą╝ ą┐čĆąĖą╗ąŠąČąĄąĮąĖąĖ ą┐čĆąĖą┤ąĄčéčüčÅ čćąĖčéą░čéčī ąÉą”ą¤ ą▓ ąŠą▒čĆą░ą▒ąŠčéčćąĖą║ąĄ čéą░ą╣ą╝ąĄčĆą░, ąĖ ąĮą░ą▓ąĄčĆąĮąŠąĄ čéą░ą╝ ąČąĄ ą┤ąĄą╗ą░čéčī ą▓čŗąĘąŠą▓ čäčāąĮą║čåąĖąĖ FIR), č鹊 ą│čĆčāą▒ąŠ ą┐čĆąĖą┤ąĄčéčüčÅ ą┤ąŠą▒ą░ą▓ąĖčéčī ąĄčēąĄ 10 čåąĖą║ą╗ąŠą▓. ąśč鹊ą│ąŠ, ąĖą╝ąĄąĄą╝ 90+10=100 čåąĖą║ą╗ąŠą▓ čÅą┤čĆą░, ą║ąŠč鹊čĆčŗąĄ ąĘą░ąĮąĖą╝ą░ąĄčé ąŠą▒čĆą░ą▒ąŠčéą║ą░ ąŠą┤ąĮąŠą╣ ą▓čŗą▒ąŠčĆą║ąĖ ąÉą”ą¤. ą¦č鹊 čŹč鹊 ąŠąĘąĮą░čćą░ąĄčé? ąŁč鹊 ą║ą░ą║ čĆą░ąĘ ąĖ ąĄčüčéčī ąŠą│čĆą░ąĮąĖč湥ąĮąĖąĄ ą┐ąŠ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą▓ąŠąĘą╝ąŠąČąĮąŠą╣ čćą░čüč鹊č鹥 ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ čüąĖčüč鹥ą╝čŗ Fs, ą║ąŠč鹊čĆą░čÅ ą║ą░ą║ čĆą░ąĘ ąĖ ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčé ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčāčÄ čćą░čüč鹊čéčā čüąĖą│ąĮą░ą╗ą░, ą║ąŠč鹊čĆčāčÄ ą╝ąŠąČąĄčé ą┐čĆąŠą┐čāčüčéąĖčéčī č湥čĆąĄąĘ čüąĄą▒čÅ čäąĖą╗čīčéčĆ (ą┐ąŠ č鹥ąŠčĆąĄą╝ąĄ ąÜąŠč鹥ą╗čīąĮąĖą║ąŠą▓ą░ Fs/2).
ąśčéą░ą║, ąŠčüčéą░ąĄčéčüčÅ č鹊ą╗čīą║ąŠ ą▓čŗčćąĖčüą╗ąĖčéčī čŹčéčā ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠ ą▓ąŠąĘą╝ąŠąČąĮčāčÄ čćą░čüč鹊čéčā ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ Fs, ąĖ č鹊ą│ą┤ą░ čüčĆą░ąĘčā čüčéą░ąĮąĄčé ą┐ąŠąĮčÅčéąĮąŠ, čćč鹊 ą╝čŗ ą╝ąŠąČąĄą╝, ą░ čćč鹊 ąĮąĄčé. ą»ą┤čĆąŠ AVR čĆą░ą▒ąŠčéą░ąĄčé ąĮą░ čćą░čüč鹊č鹥 20 ą£ąōčå, čé. ąĄ. ą▓ čüąĄą║čāąĮą┤čā ą▓čŗą┐ąŠą╗ąĮčÅąĄčé 20000000 čåąĖą║ą╗ąŠą▓. ąŻ ąĮą░čü ą┐čĆąŠą║čĆčāčéą║ą░ čäąĖą╗čīčéčĆą░ ąĘą░ąĮąĖą╝ą░ąĄčé 100 čåąĖą║ą╗ąŠą▓, čé. ąĄ. ąĘą░ čüąĄą║čāąĮą┤čā ą╝čŗ ą╝ąŠąČąĄą╝ čüą┤ąĄą╗ą░čéčī 20000000/100 = 200000 ą┐čĆąŠą║čĆčāč鹊ą║, čé. ąĄ. čćą░čüč鹊čéą░ ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ Fs čā ąĮą░čü ą╝ąŠąČąĄčé ą▒čŗčéčī 200000 ąōčå, ąĖą╗ąĖ 200 ą║ąōčå. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ą╝čŗ ą╝ąŠąČąĄą╝ ą┐čĆąŠą┐čāčüą║ą░čéčī č湥čĆąĄąĘ čäąĖą╗čīčéčĆ čćą░čüč鹊čéčŗ ą┤ąŠ 100000 ą║ąōčå. ąŚą▓čāčćąĖčé, ą║ąŠąĮąĄčćąĮąŠ, ą║čĆčāč鹊, ąŠą┤ąĮą░ą║ąŠ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ą┐ąŠą╝ąĮąĖčéčī, čćč鹊 čŹč鹊 ą┐ąŠą┤čüč湥čé ą┤ą╗čÅ ąĖą┤ąĄą░ą╗čīąĮąŠą│ąŠ čüą╗čāčćą░čÅ - ą║ąŠą│ą┤ą░ AVR čā ąĮą░čü ąĮąĖč湥ą│ąŠ, ą║čĆąŠą╝ąĄ čĆą░čüč湥čéą░ čäąĖą╗čīčéčĆą░, ąĮąĄ ą┤ąĄą╗ą░ąĄčé, ą░ čéą░ą║ ą▓ čĆąĄą░ą╗čīąĮąŠą╣ ąČąĖąĘąĮąĖ, čāą▓čŗ, ąĮąĄ ą▒čŗą▓ą░ąĄčé. ąÆąĄą┤čī ąĮą░ą┤ąŠ ąĄčēąĄ ąĖ ąŠą┐čĆą░čłąĖą▓ą░čéčī ą┤ą░čéčćąĖą║ąĖ, ą║ąĮąŠą┐ą║ąĖ, ą╝ąĖą│ą░čéčī čüą▓ąĄč鹊ą┤ąĖąŠą┤ą░ą╝ąĖ ąĖ ą▓ąŠąŠą▒čēąĄ ą▓čŗą┐ąŠą╗ąĮčÅčéčī ą║ą░ą║ąŠą╣-ąĮąĖą║ą░ą║ąŠą╣ ąŠą▒čēąĖą╣ č乊ąĮąŠą▓čŗą╣ ą░ą╗ą│ąŠčĆąĖčéą╝. ąÆ ąĖč鹊ą│ąĄ ą┐čĆąĖą╝ąĄčĆąĮąŠ ą┐ąŠą╗čāčćąĖą╝ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčāčÄ Fs ąŠą║ąŠą╗ąŠ 100 ą║ąōčå, čé. ąĄ. ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčŗą╣ ą▓čģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗ - ą┤ąŠ 50 ą║ąōčå. ąÆčüąĄ čĆą░ą▓ąĮąŠ čćč鹊-č鹊 čüą╗ąĖčłą║ąŠą╝ ą║čĆčāč鹊...
ąĢčüą╗ąĖ ą▓ą┤čĆčāą│ ąĘą░čģąŠčéąĖą╝ čäąĖą╗čīčéčĆ ąĮąĄ 4-ą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░, ą░ 8-ą│ąŠ, č鹊 ą┐ąŠąĮčÅčéąĮąŠ, čćč鹊 ą▓čüąĄ ą░ą▓č鹊ą╝ą░čéąĖč湥čüą║ąĖ čāčģčāą┤čłą░ąĄčéčüčÅ ą▓ ą┤ą▓ą░ čĆą░ąĘą░ - ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ Fs 50 ą║ąōčå, ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ ą▓čģąŠą┤ąĮą░čÅ čćą░čüč鹊čéą░ 25 ą║ąōčå ąĖ čéą░ą║ ą┤ą░ą╗ąĄąĄ. ąØą░ą┤ąĄčÄčüčī, č鹥ą┐ąĄčĆčī ąÆčŗ ą▓ čüąŠčüč鹊čÅąĮąĖąĖ ąŠčåąĄąĮąĖčéčī ą▓ąŠąĘą╝ąŠąČąĮąŠčüčéąĖ čåąĖčäčĆąŠą▓ąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ąĮą░ AVR.
2. ąØąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ąĮąĄ ąĘą░ą▒čŗą▓ą░čéčī ą▓ą░ąČąĮąŠąĄ čāčüą╗ąŠą▓ąĖąĄ - ąĮąĖ ą▓ ą║ąŠąĄą╝ čüą╗čāčćą░ąĄ ąĮąĄą╗čīąĘčÅ ąĮą░ ą▓čģąŠą┤ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░ ą┐ąŠą┤ą░ą▓ą░čéčī čćą░čüč鹊čéčŗ ą▓čŗčłąĄ č湥ą╝ Fs/2, ąĖąĮą░č湥 čŹč鹊 čćčĆąĄą▓ą░č鹊 ą│čĆčāą▒čŗą╝ąĖ ąŠčłąĖą▒ą║ą░ą╝ąĖ ą▓ čĆą░ą▒ąŠč鹥 čäąĖą╗čīčéčĆą░ (ąĮąĄ čüą┐čĆą░čłąĖą▓ą░ą╣č鹥 ą╝ąĄąĮčÅ, ą┐ąŠč湥ą╝čā - ą▓ čāą╝ąĮčŗčģ ą║ąĮąĖąČą║ą░čģ ą▓čüąĄ ąĮą░ą┐ąĖčüą░ąĮąŠ). ą¦č鹊ą▒čŗ ą▓čŗą┐ąŠą╗ąĮąĖčéčī čŹč鹊 čāčüą╗ąŠą▓ąĖąĄ, ąĮą░ ą▓čģąŠą┤ąĄ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░ ą▓čüąĄą│ą┤ą░ čüčéą░ą▓čÅčé ą┐čĆąĄą┤ą▓ą░čĆąĖč鹥ą╗čīąĮčŗą╣ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗą╣ čäąĖą╗čīčéčĆ ąĮąĖąĘą║ąŠą╣ čćą░čüč鹊čéčŗ čü čćą░čüč鹊č鹊ą╣ čüčĆąĄąĘą░ Fs/2 ąĖą╗ąĖ ąĮąĖąČąĄ (čģąŠčéčÅ ą▒čŗ ą┐čĆąŠčüčéčāčÄ RC-čåąĄą┐ąŠčćą║čā). ąśąĮą░č湥 - ąĮąĖą║ą░ą║. ąÜą░ą║ą░čÅ ąĖčĆąŠąĮąĖčÅ - čćč鹊ą▒čŗ čåąĖčäčĆąŠą▓ąŠą╣ čäąĖą╗čīčéčĆ čĆą░ą▒ąŠčéą░ą╗, ąĮą░ ąĄą│ąŠ ą▓čģąŠą┤ąĄ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ąŠą▒čÅąĘą░č鹥ą╗čīąĮąŠ čüčéą░čĆčŗą╣ ą┤ąŠą▒čĆčŗą╣ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗą╣ čäąĖą╗čīčéčĆ... ą¤ąŠąĮčÅčéąĮąŠ, čćč鹊 č湥ą╝ ą╝ąĄąĮčīčłąĄ čćą░čüč鹊čéą░ čüčĆąĄąĘą░ ą░ąĮą░ą╗ąŠą│ąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░ ą┐ąŠ ąŠčéąĮąŠčłąĄąĮąĖčÄ ą║ Fs/2, č鹥ą╝ ąĮą░ą┤ąĄąČąĮąĄąĄ ą▒čāą┤ąĄčé ą┐ąŠą┤ą░ą▓ą╗ąĄąĮąĖąĄ ą┐ą░čĆą░ąĘąĖčéąĮčŗčģ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ čüąĖą│ąĮą░ą╗ą░, ąĖ č鹥ą╝ čüąĖą╗čīąĮąĄąĄ ą╝ąŠąČąĮąŠ čāą┐čĆąŠčüčéąĖčéčī čüčģąĄą╝čā ą░ąĮą░ą╗ąŠą│ąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░. ą¤ąŠčŹč鹊ą╝čā ąĄčüą╗ąĖ čģąŠčéąĖą╝ čüąŠą▓čüąĄą╝ ą┐čĆąŠčüčéčāčÄ čüčģąĄą╝čā, č鹊 ą┐ąŠą╗ąŠčüą░ ą┤ąŠą┐čāčüčéąĖą╝ąŠą│ąŠ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ čāą╝ąĄąĮčīčłą░ąĄčéčüčÅ ąĄčēąĄ ą▒ąŠą╗čīčłąĄ - ą▓ ą┤ą▓ą░, ą▓ č湥čéčŗčĆąĄ čĆą░ąĘą░ ą┐ąŠ ąŠčéąĮąŠčłąĄąĮąĖčÄ ą║ Fs/2. ąÆ ąĖą┤ąĄą░ą╗ąĄ ą▓čģąŠą┤ąĮąŠą╣ čäąĖą╗čīčéčĆ ą┤ąŠą╗ąČąĄąĮ ąŠčüą╗ą░ą▒ą╗čÅčéčī čüąĖą│ąĮą░ą╗ ą▓ ą┐ą░čĆą░ąĘąĖčéąĮąŠą╝ ą┤ą╗čÅ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ą┤ąŠ čāčĆąŠą▓ąĮčÅ ąĄą┤ąĖąĮąĖčåčŗ ą╝ą╗ą░ą┤čłąĄą│ąŠ čĆą░ąĘčĆčÅą┤ą░ ąÉą”ą¤ (čé. ąĄ. ą┤ą╗čÅ 10-ą▒ąĖčéąĮąŠą│ąŠ ąÉą”ą¤ ą▓čģąŠą┤ąĮąŠą╣ čäąĖą╗čīčéčĆ ą┤ąŠą╗ąČąĄąĮ ą┤ą░ą▓ą░čéčī ąŠčüą╗ą░ą▒ą╗ąĄąĮąĖąĄ ąĮąĄąĮčāąČąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ ą▓ 210 čĆą░ąĘ, ąĖą╗ąĖ 60 ą┤ąæ). ąó. ąĄ. čĆąĄą░ą╗čīąĮąŠ ąĮą░ čćą░čüč鹊č鹥 ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ 100 ą║ąōčå čāą┤ąŠą▒ąĮąŠ ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░čéčī čćą░čüč鹊čéčŗ ąĮąĄ ą▓čŗčłąĄ 4..8 ą║ąōčå, ąĖąĮą░č湥 ą┐čĆąĖą┤ąĄčéčüčÅ ą│ąŠčĆąŠą┤ąĖčéčī čüą╗ąŠąČąĮčŗąĄ ą╝ąĮąŠą│ąŠčüčéčāą┐ąĄąĮčćą░čéčŗąĄ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗąĄ čäąĖą╗čīčéčĆčŗ... ąØčā ąĖ ąĘą░čüą░ą┤ą░. ąóąĄą┐ąĄčĆčī ą┐ąŠąĮčÅčéąĮąŠ, ą┐ąŠč湥ą╝čā AVR ąĄčēąĄ ąĮąĄ "čāą▒ąĖą╣čåą░" ą║ą╗ą░čüčüąĖč湥čüą║ąĖčģ ą┤ąŠčĆąŠą│čāčēąĖčģ DSP - ąĘą░ ą▓čüąĄ ąĮą░ą┤ąŠ ą┐ą╗ą░čéąĖčéčī, čĆąŠąĘąŠą▓čŗąĄ ąŠčćą║ąĖ čüąĮčÅčéčŗ. ąóą░ą║ čćč鹊 AVR ą▓ čåąĖčäčĆąŠą▓ąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ - ą▓ąŠą▓čüąĄ ąĮąĄ ą┐ą░ąĮą░čåąĄčÅ ąŠčé ą▓čüąĄčģ ą┐čĆąŠą▒ą╗ąĄą╝, ąĮąŠ AVR ą▓ą┐ąŠą╗ąĮąĄ ą╝ąŠąČąĄčé ąĮą░ą╣čéąĖ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄ ą▓ čĆą░ą┤ąĖąŠą╗čÄą▒ąĖč鹥ą╗čīčüą║ąŠą╣ ą┐čĆą░ą║čéąĖą║ąĄ ą┤ą╗čÅ ą│čĆčāą▒ąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ąĘą▓čāą║ą░ (10 ą▒ąĖčé ąĮąĄ ą░čģčéąĖ ą║ą░ą║ą░čÅ č鹊čćąĮąŠčüčéčī) ąĖą╗ąĖ - čćč鹊 ąĄčēąĄ ą╗čāčćčłąĄ - ą┤ą╗čÅ ą┤ąĄą║ąŠą┤ąĖčĆąŠą▓ą░ąĮąĖčÅ čüąĖą│ąĮą░ą╗ąŠą▓ č鹥ą╗ąĄčāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ.
ąöą╗čÅ čĆą░čüč湥čéą░ ą▓čģąŠą┤ąĮčŗčģ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓ ą╝ąŠąČąĮąŠ ą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ą│ąŠč鹊ą▓čŗą╝ąĖ ąĖąĮčüčéčĆčāą╝ąĄąĮčéą░ą╝ąĖ - č鹥ą╝ ąČąĄ Matlab ąĖą╗ąĖ, čćč鹊 ąĄčēąĄ ą╗čāčćčłąĄ, ąŠąĮą╗ą░ą╣ąĮ čāčéąĖą╗ąĖčéą░ą╝ąĖ ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ WEBENCH ąŠčé National Semiconductor (čüą╝. [7]).
3. ąöą╗čÅ čāąĘą║ąŠčüą┐ąĄčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮąĮčŗčģ čäąĖą╗čīčéčĆąŠą▓ ą╝ąŠąČąĮąŠ ą┐čĆąĖą╝ąĄąĮąĖčéčī ą┤ą░ąČąĄ ąŠą┤ąĮąŠą▒ąĖčéąĮąŠąĄ ą░ąĮą░ą╗ąŠą│ąŠą▓ąŠ-čåąĖčäčĆąŠą▓ąŠąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖąĄ (čü ą┐ąŠą╝ąŠčēčīčÄ ą║ąŠą╝ą┐ą░čĆą░č鹊čĆą░). ąØą░ą┐čĆąĖą╝ąĄčĆ, čéą░ą║ąŠąĄ čĆąĄčłąĄąĮąĖąĄ ą▓ą┐ąŠą╗ąĮąĄ ą┐ąŠą┤čģąŠą┤ąĖčé ą┤ą╗čÅ č鹊ąĮą░ą╗čīąĮčŗčģ ą┤ąĄą║ąŠą┤ąĄčĆąŠą▓ (DTMF ąĖ čé. ą┐.). ą¤čĆąĖ čŹč鹊ą╝ ą║ąŠą┤ ą╝ąŠąČąĮąŠ čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ąŠą┐čéąĖą╝ąĖąĘąĖčĆąŠą▓ą░čéčī ą┐ąŠą┤ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ ą║ąŠąĮą║čĆąĄčéąĮąŠą╣ ąĘą░ą┤ą░čćąĖ - ąĮą░ą┐čĆąĖą╝ąĄčĆ, ą▓ čüą╗čāčćą░ąĄ ą┤ąĄą║ąŠą┤ąĄčĆą░ DTMF ą┐čĆąŠčüčćąĖčéčŗą▓ą░čéčī čüčĆą░ąĘčā 8 ą┐ąŠą╗ąŠčüąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓ ą┤ą╗čÅ č鹊ąĮą░ą╗čīąĮčŗčģ čćą░čüč鹊čé.
ąöą╗čÅ čĆą░čüč湥čéą░ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓ (ai, bj) ą╝ąŠąČąĮąŠ ąŠą┐čÅčéčī-čéą░ą║ąĖ ą┐čĆąĖą╝ąĄąĮąĖčéčī ąŠąĮą╗ą░ą╣ąĮ-ąĖąĮčüčéčĆčāą╝ąĄąĮčéčŗ (čüą╝. [4], [5], [6], [9]).
[ąĪčüčŗą╗ą║ąĖ]
1. ŌĆ£Discrete-Time signal processingŌĆØ, A. V. Oppenheimer & R. W. Schafer. Prentice-Hall International Inc. 1989. ISBN 0-13-216771-9
2. ŌĆ£Introduction to Signal ProcessingŌĆØ, S. J. Orfanidis, Prentice Hall International Inc., 1996. ISBN 0-13-240334-X
3. FIR filter design, http://www.iowegian.com/scopefir.htm
4. FIR filter design, http://www.dsptutor.freeuk.com/FIRFilterDesign/FIRFiltDes102.html
5. FIR filter design, http://www.dsptutor.freeuk.com/KaiserFilterDesign/KaiserFilterDesign.html
6. FIR and IIR filter design, http://www-users.cs.york.ac.uk/~fisher/mkfilter/
7. WEBENCH® Designer Tools site:national.com.
8. ą¤čĆąŠąĄą║čéąĖčĆąŠą▓ą░ąĮąĖąĄ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓ site:model.exponenta.ru.
9. ą×ąĮą╗ą░ą╣ąĮ čĆą░čüč湥čé čäąĖą╗čīčéčĆąŠą▓ čĆą░ąĘąĮąŠą│ąŠ ą▓ąĖą┤ą░ (ą░ą┐ą┐ą╗ąĄčé JAVA) - ąæą░čéč鹥čĆą▓ąŠčĆčé, ą¦ąĄą▒čŗčłąĄą▓, 菹╗ą╗ąĖą┐čéąĖč湥čüą║ąĖą╣, ąæąĄčüčüąĄą╗čī, ąÜą░ą╣ąĘąĄčĆ.
10. ąÆ ą░čĆčģąĖą▓ąĄ: ąÉ.ąæ. ąĪąĄčĆą│ąĖąĄąĮą║ąŠ. ą”ąĖčäčĆąŠą▓ą░čÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░ čüąĖą│ąĮą░ą╗ąŠą▓. ąśąĘą┤. ą¤ąĖč鹥čĆ, ąŻč湥ą▒ąĮąĖą║ ą┤ą╗čÅ ą▓čāąĘąŠą▓, 2002 ą│., ISBN 5-318-00666-3. ąÉą╣čäąĖč湥čĆ ąŁ.ąĪ., ąöąČąĄčĆą▓ąĖčü ąæ.ąŻ. ą”ąĖčäčĆąŠą▓ą░čÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░ čüąĖą│ąĮą░ą╗ąŠą▓: ą┐čĆą░ą║čéąĖč湥čüą║ąĖą╣ ą┐ąŠą┤čģąŠą┤. 2004 ą│. ISBN 7-8459-0710-1 ąĖ ą╝ąĮąŠą│ąĖąĄ ą┤čĆčāą│ąĖąĄ ą║ąĮąĖą│ąĖ ą┐ąŠ čåąĖčäčĆąŠą▓ąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ čüąĖą│ąĮą░ą╗ąŠą▓.
11. ąśčüčģąŠą┤ąĮąĖą║ąĖ ą┐čĆąĖą╝ąĄčĆąŠą▓ ąĖąĘ ą░ą┐ąĮąŠčāčéą░ AVR223 čü ą┐ąĄčĆąĄą▓ąĄą┤ąĄąĮąĮčŗą╝ąĖ ąĮą░ čĆčāčüčüą║ąĖą╣ čÅąĘčŗą║ ą║ąŠą╝ą╝ąĄąĮčéą░čĆąĖčÅą╝ąĖ. ąś ąĄčēąĄ ąĮąĄčüą║ąŠą╗čīą║ąŠ ą╗čāčćčłąĖčģ, ą║ą░ą║ ą╝ąĮąĄ ą║ą░ąČąĄčéčüčÅ, ą║ąĮąĖąČąĄą║ ą┐ąŠ ą”ą×ąĪ.
12. Kaiser window FIR filter design site:mathworks.com. |

ąÜąŠą╝ą╝ąĄąĮčéą░čĆąĖąĖ
microsin: ąĄčüą╗ąĖ ą┐ąŠą┐ą░ą┤ąĄčéčüčÅ čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĖą╣ ą░ą┐ąĮąŠčāčé, č鹊 ąĄą│ąŠ ą┐ąĄčĆąĄą▓ąŠą┤ ą▓ ą▓ąĖą┤ąĄ čüčéą░čéčīąĖ ąŠą▒čÅąĘą░č鹥ą╗čīąĮąŠ ą┐ąŠčÅą▓ąĖčéčüčÅ. ąØąŠ čāą▓čŗ... ą¤ąŠą║ą░ ąĄčüčéčī č鹊ą╗čīą║ąŠ ą░ą┐ąĮąŠčāčé ą┤ą╗čÅ PIC AN542, ą║ąŠč鹊čĆčŗą╣ ąĮąĄ ąĮą░čüč鹊ą╗čīą║ąŠ ąĖąĮč鹥čĆąĄčüąĄąĮ ą┤ą╗čÅ ą┐ąĄčĆąĄą▓ąŠą┤ą░.
microsin: ą┤ą╗čÅ ą╗čÄą▒ąŠą╣ čåąĖčäčĆąŠą▓ąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ ąĘą▓čāą║ą░. ąØą░ą┐čĆąĖą╝ąĄčĆ, ąÆą░ą╝ ąĮčāąČąĮąŠ ą▓čŗą┤ąĄą╗ąĖčéčī ąĖąĘ čüąĖą│ąĮą░ą╗ą░, ąĘą░ą│čĆčÅąĘąĮąĄąĮąĮąŠą│ąŠ čłčāą╝ą░ą╝ąĖ, čüąĖą│ąĮą░ą╗ čü ąĖąĘą▓ąĄčüčéąĮąŠą╣ ąÆą░ą╝ čćą░čüč鹊č鹊ą╣. ąŁč鹊 ą║ą░ą║ čĆą░ąĘ ąĖ ą╝ąŠąČąĄčé čåąĖčäčĆąŠą▓ąŠą╣ čäąĖą╗čīčéčĆ - ą▓čŗą┤ąĄą╗ąĖčéčī ąŠą┤ąĖąĮ ą┤ąĖą░ą┐ą░ąĘąŠąĮ čüą┐ąĄą║čéčĆą░ ąĖ ąŠčüą╗ą░ą▒ąĖčéčī ą┤čĆčāą│ąŠą╣. ąŁč鹊 ą┐čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ čéą░ą║ąČąĄ ą▓ č鹊ąĮą░ą╗čīąĮąŠą╝ č鹥ą╗ąĄčāą┐čĆą░ą▓ą╗ąĄąĮąĖąĖ (ąĮą░ą┐čĆąĖą╝ąĄčĆ, č鹊čé ąČąĄ DTMF), čĆą░čüą┐ąŠąĘąĮą░ą▓ą░ąĮąĖąĖ čüąĖą│ąĮą░ą╗ąŠą▓ ąŠčéą▒ąŠčÅ ąÉąóąĪ (PBX). ą£ąŠąČąĮąŠ, ąĮą░ą┐čĆąĖą╝ąĄčĆ, čüą┤ąĄą╗ą░čéčī čĆą░ąĘą┤ąĄą╗ąĄąĮąĖąĄ ą║ą░ąĮą░ą╗ąŠą▓ ą┤ą╗čÅ čåą▓ąĄč鹊ą╝čāąĘčŗą║ąĖ.
RSS ą╗ąĄąĮčéą░ ą║ąŠą╝ą╝ąĄąĮčéą░čĆąĖąĄą▓ čŹč鹊ą╣ ąĘą░ą┐ąĖčüąĖ