|
ąŚą┤ąĄčüčī ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą┐ąĄčĆąĄą▓ąŠą┤ ą░ą┐ąĮąŠčāčéą░ AVR221: Discrete PID controller on tinyAVR and megaAVR devices [1] (ą┤ąĖčüą║čĆąĄčéąĮčŗą╣ ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ PID ąĮą░ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░čģ čüąĄčĆąĖą╣ tinyAVR ąĖ megaAVR).
ąÆąŠąĘą╝ąŠąČąĮąŠčüčéąĖ ąŠą┐ąĖčüą░ąĮąĮąŠą│ąŠ ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░:
ŌĆó ą¤čĆąŠčüč鹊ą╣ ą┤ąĖčüą║čĆąĄčéąĮčŗą╣ (čåąĖčäčĆąŠą▓ąŠą╣) ą░ą╗ą│ąŠčĆąĖčéą╝ PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░
ŌĆó ą£ąŠąČąĮąŠ čĆąĄą░ą╗ąĖąĘąŠą▓ą░čéčī ąĮą░ ą▓čüąĄčģ ą╝ąŠą┤ąĄą╗čÅčģ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓ AVR
ŌĆó ążčāąĮą║čåąĖčÅ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ PID ąĖčüą┐ąŠą╗čīąĘčāąĄčé 534 ą▒ą░ą╣čéą░ ą┐ą░ą╝čÅčéąĖ ą┐čĆąŠą│čĆą░ą╝ą╝ (FLASH) ąĖ čéčĆąĄą▒čāąĄčé 877 čåąĖą║ą╗ąŠą▓ CPU (ą┐čĆąĖą╝ąĄąĮąĄąĮ ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆ IAR, ą▓ą║ą╗čÄč湥ąĮą░ ąŠą┐čéąĖą╝ąĖąĘą░čåąĖčÅ ą┐ąŠ čĆą░ąĘą╝ąĄčĆčā ą║ąŠą┤ą░)
[1 ąöą╗čÅ č湥ą│ąŠ ąĮčāąČąĄąĮ PID-čĆąĄą│čāą╗čÅč鹊čĆ?]
ąŁč鹊čé ą░ą┐ąĮąŠčāčé ąŠą┐ąĖčüčŗą▓ą░ąĄčé ą┐čĆąŠčüčéčāčÄ čĆąĄą░ą╗ąĖąĘą░čåąĖčÄ ą┤ąĖčüą║čĆąĄčéąĮąŠą│ąŠ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠ-ąĖąĮč鹥ą│čĆą░ą╗čīąĮąŠ-ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠą│ąŠ (ą┤ąŠčüą╗ąŠą▓ąĮčŗą╣ ą┐ąĄčĆąĄą▓ąŠą┤ Proportional-Integral-Derivative, PID) ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░.
ąÜąŠą│ą┤ą░ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ą┐čĆąĖą╝ąĄąĮąĖčéčī čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖąĄ ą▓čŗčģąŠą┤ą░ čüąĖčüč鹥ą╝čŗ, ąŠčéčüą╗ąĄąČąĖą▓ą░čÅ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ąŠą┐ąŠčĆąĮąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ ąĖą╗ąĖ čüąŠčüč鹊čÅąĮąĖčÅ, ą╝ąŠąČąĄčé ą┐ąŠčéčĆąĄą▒ąŠą▓ą░čéčīčüčÅ ąĮąĄą║ąĖą╣ ą░ą╗ą│ąŠčĆąĖčéą╝ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ. ą¤čĆąĖą╝ąĄčĆąŠą╝ čéą░ą║ąĖčģ ą┐čĆąĖą╗ąŠąČąĄąĮąĖą╣ ą╝ąŠąČąĄčé čüą╗čāąČąĖčéčī čāą┐čĆą░ą▓ą╗ąĄąĮąĖąĄ ą╝ąŠč鹊čĆąŠą╝, ą┐ąŠą┤ą┤ąĄčƹȹĖą▓ą░ąĮąĖąĄ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ ą▓ ą┐ąĄčćąĖ, čüčéą░ą▒ąĖą╗ąĖąĘą░čåąĖčÅ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ, ą┤ą░ą▓ą╗ąĄąĮąĖčÅ, ą┐ąŠč鹊ą║ą░ ąČąĖą┤ą║ąŠčüčéąĖ, čüą║ąŠčĆąŠčüčéąĖ, čāčüą║ąŠčĆąĄąĮąĖčÅ ąĖą╗ąĖ ą┤čĆčāą│ąĖčģ ąĘąĮą░č湥ąĮąĖą╣. ą×ą┤ąĮąĖą╝ ąĖąĘ čéą░ą║ąĖčģ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ čÅą▓ą╗čÅąĄčéčüčÅ PID, ą║ąŠč鹊čĆčŗą╣ ą╝ąŠąČąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ ą┤ą╗čÅ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą╗čÄą▒ąŠą╣ ąĖąĘą╝ąĄčĆčÅąĄą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮąŠą╣, ą║ąŠą│ą┤ą░ ąŠąĮą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ąĘą░čéčĆąŠąĮčāčéą░ ą┐čĆąĖ ą╝ą░ąĮąĖą┐čāą╗ąĖčĆąŠą▓ą░ąĮąĖąĖ ą┤čĆčāą│ąĖą╝ąĖ ą┐ąĄčĆąĄą╝ąĄąĮąĮčŗą╝ąĖ ą┐čĆąŠčåąĄčüčüą░.
ąŚą░ ą▓čüąĄ ą▓čĆąĄą╝čÅ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ąŠčüčī ą╝ąĮąŠą│ąŠ čĆąĄčłąĄąĮąĖą╣ ą┤ą╗čÅ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, ąĮąŠ ą▓ čüčĆą░ą▓ąĮąĄąĮąĖąĖ čüąŠ ą▓čüąĄą╝ąĖ PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ ą┐ąŠą╗čāčćąĖą╗ čĆąĄą┐čāčéą░čåąĖčÄ "ąĖąĮą┤čāčüčéčĆąĖą░ą╗čīąĮąŠą│ąŠ čüčéą░ąĮą┤ą░čĆčéą░" ąĖąĘ-ąĘą░ čüą▓ąŠąĄą╣ ą┐čĆąŠčüč鹊čéčŗ ąĖ čģąŠčĆąŠčłąĄą│ąŠ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ. ą¦č鹊ą▒čŗ ą┐ąŠą╗čāčćąĖčéčī ą▒ąŠą╗čīčłąĄ ąĖąĮč乊čĆą╝ą░čåąĖąĖ ą┐ąŠ ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ą╝ PID ąĖčģ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖčÄ, ąŠą▒čĆą░čéąĖč鹥čüčī ą║ ą┤čĆčāą│ąĖą╝ ąĖčüč鹊čćąĮąĖą║ą░ą╝, ąĮą░ą┐čĆąĖą╝ąĄčĆ ą║ ą║ąĮąĖą│ąĄ "PID Controllers" K. J. Astrom & T. Hagglund (1995).
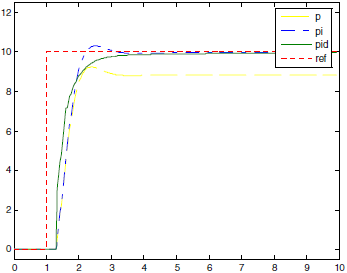
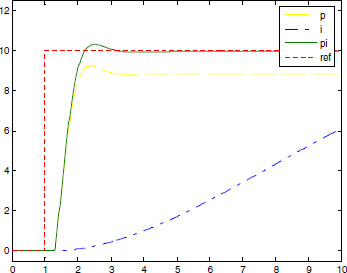
ąĀąĖčü. 1-1. ąóąĖą┐ąĖčćąĮčŗą╣ ąŠčéą║ą╗ąĖą║ PID-čĆąĄą│čāą╗čÅč鹊čĆą░ ąĮą░ čüą║ą░čćą║ąŠąŠą▒čĆą░ąĘąĮąŠąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ą▓čģąŠą┤ąĮąŠą╣ ąŠą┐ąŠčĆąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ.
ą¤čĆąĖą╝ąĄčćą░ąĮąĖąĄ ą║ čĆąĖčü. 1-1: ref - ą▓čģąŠą┤ąĮąŠąĄ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠąĄ ą▓ąŠąĘą┤ąĄą╣čüčéą▓ąĖąĄ, pi - ąŠčéą║ą╗ąĖą║ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠ-ąĖąĮč鹥ą│čĆą░ą╗čīąĮąŠą│ąŠ čĆąĄą│čāą╗čÅč鹊čĆą░, p - ąŠčéą║ą╗ąĖą║ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠą│ąŠ čĆąĄą│čāą╗čÅč鹊čĆą░, pid - ąŠčéą║ą╗ąĖą║ PID-čĆąĄą│čāą╗čÅč鹊čĆą░.
[2 PID-čĆąĄą│čāą╗čÅč鹊čĆ]
ąØą░ čĆąĖčü. 2-1 čüčģąĄą╝ą░čéąĖčćąĮąŠ ą┐ąŠą║ą░ąĘą░ąĮą░ čüąĖčüč鹥ą╝ą░ čü PID-čĆąĄą│čāą╗čÅč鹊čĆąŠą╝. PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ čüčĆą░ą▓ąĮąĖą▓ą░ąĄčé ąĖąĘą╝ąĄčĆąĄąĮąĮčāčÄ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝čāčÄ ą▓ąĄą╗ąĖčćąĖąĮčā y čü ąŠą┐ąŠčĆąĮčŗą╝ ąĘąĮą░č湥ąĮąĖąĄ y0. ąĀą░ąĘąĮąŠčüčéčī (ąĖą╗ąĖ ąŠčłąĖą▒ą║ą░) e ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░ąĄčéčüčÅ ą┤ą╗čÅ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ąĮąŠą▓ąŠą│ąŠ ą▓čģąŠą┤ąĮąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ ą┤ą╗čÅ čüąĖčüč鹥ą╝čŗ u. ąŁč鹊 ą▓čģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ą┐čŗčéą░ąĄčéčüčÅ ą┐ąŠą┤čüčéčĆąŠąĖčéčī ąĖąĘą╝ąĄčĆčÅąĄą╝čāčÄ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝čāčÄ ą▓ąĄą╗ąĖčćąĖąĮčā čéą░ą║, čćč鹊ą▒čŗ ąŠąĮą░ ą▓ąĄčĆąĮčāą╗ą░čüčī ą▓ ąĮčāąČąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ, čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĄąĄ ąŠą┐ąŠčĆąĮąŠą╝čā. ą¤ąŠą╗čāčćą░ąĄčéčüčÅ čüčģąĄą╝ą░ čü ąĘą░ą╝ą║ąĮčāčéčŗą╝ čåąĖą║ą╗ąŠą╝ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ (čāą┐čĆą░ą▓ą╗ąĄąĮąĖąĄ čü ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘčīčÄ).
ąÉą╗čīč鹥čĆąĮą░čéąĖą▓ąŠą╣ čüčģąĄą╝ąĄ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ čü ąĘą░ą╝ą║ąĮčāč鹊ą╣ ą┐ąĄčéą╗ąĄą╣ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ čÅą▓ą╗čÅąĄčéčüčÅ čüčģąĄą╝ą░ ąŠčéą║čĆčŗč鹊ą│ąŠ čåąĖą║ą╗ą░ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ (ą▒ąĄąĘ ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘąĖ). ąóą░ą║ą░čÅ čüčģąĄą╝ą░ ą┐čĆąŠčēąĄ, ąĮąŠ ą▓ąŠ ą╝ąĮąŠą│ąĖčģ čüą╗čāčćą░čÅčģ čÅą▓ą╗čÅąĄčéčüčÅ ąĮąĄčāą┤ąŠą▓ą╗ąĄčéą▓ąŠčĆąĖč鹥ą╗čīąĮąŠą╣, ąĖ ąĄčæ čćą░čüč鹊 ąĮąĄą▓ąŠąĘą╝ąŠąČąĮąŠ čĆąĄą░ą╗ąĖąĘąŠą▓ą░čéčī ąĖąĘ-ąĘą░ čüą▓ąŠą╣čüčéą▓ čüą░ą╝ąŠą╣ čüąĖčüč鹥ą╝čŗ. ą¤čāč鹥ą╝ ą┤ąŠą▒ą░ą▓ą╗ąĄąĮąĖčÅ ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘąĖ ą┐ąŠ ą▓čģąŠą┤čā čüąĖčüč鹥ą╝čŗ ą╝ąŠąČąĮąŠ čāą╗čāčćčłąĖčéčī ą║ą░č湥čüčéą▓ąŠ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĖ ą┤ą░ąČąĄ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖąĄ.
ąĀąĖčü. 2-1. ąŻą┐čĆą░ą▓ą╗ąĄąĮąĖąĄ čü ąŠą▒čĆą░čéąĮąŠą╣ čüą▓čÅąĘčīčÄ, čü ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄą╝ PID-čĆąĄą│čāą╗čÅč鹊čĆą░.
ąÜčĆąŠą╝ąĄ č鹊ą│ąŠ, ą▓ ąŠčéą╗ąĖčćąĖąĄ ąŠčé ą┐čĆąŠčüčéčŗčģ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ ą╝ąŠąČąĄčé čāą┐čĆą░ą▓ą╗čÅčéčī ą▓čģąŠą┤ąĮčŗą╝ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą╝ u, ąŠčüąĮąŠą▓čŗą▓ą░čÅčüčī ąĮą░ ąĖčüč鹊čĆąĖąĖ ąĖ čüą║ąŠčĆąŠčüčéąĖ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅ ąŠą┐ąŠčĆąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ y0. ąŁč鹊 ą┤ą░ąĄčé ą┐ąŠą▓čŗčłąĄąĮąĖąĄ č鹊čćąĮąŠčüčéąĖ ąĖ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéąĖ ą▓ ą╝ąĄč鹊ą┤ąĄ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ (čüą╝. čĆąĖčü. 1-1, ą│ą┤ąĄ ą▓ąĖą┤ąĮąŠ, čćč鹊 PID-čĆąĄą│čāą╗čÅč鹊čĆ ą┤ą░ąĄčé ą╝ąĄąĮčīčłąĄ ą║ąŠą╗ąĄą▒ą░ąĮąĖą╣ ą┐čĆąĖ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĮąĖąĖ ą▓čŗčģąŠą┤ąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ).
ą×čüąĮąŠą▓ąĮą░čÅ ąĖą┤ąĄčÅ čüąŠčüč鹊ąĖčé ą▓ č鹊ą╝, ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ čćąĖčéą░ąĄčé čüąŠčüč鹊čÅąĮąĖąĄ ą║ą░ą║ąŠą│ąŠ-č鹊 čüąĄąĮčüąŠčĆą░. ąŚą░č鹥ą╝ ąŠąĮ ą▓čŗčćąĖčéą░ąĄčé ąĖąĘą╝ąĄčĆąĄąĮąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĖąĘ ąŠą┐ąŠčĆąĮąŠą│ąŠ, ąĖ ąĖąĘ čŹč鹊ą│ąŠ ą┐ąŠą╗čāčćą░ąĄčéčüčÅ ąĘąĮą░č湥ąĮąĖąĄ ąŠčłąĖą▒ą║ąĖ. ąŁčéą░ ąŠčłąĖą▒ą║ą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ąŠą▒čĆą░ą▒ąŠčéą░ąĮą░ čéčĆąĄą╝čÅ čüą┐ąŠčüąŠą▒ą░ą╝ąĖ:
ŌĆó ąŠčéčüą╗ąĄąČąĖą▓ą░ąĮąĖąĄ č鹥ą║čāčēąĄą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ, ąĖčüą┐ąŠą╗čīąĘčāčÅ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠąĄ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖąĄ
ŌĆó ą▓ąŠčüčüčéą░ąĮąŠą▓ą╗ąĄąĮąĖąĄ ąĮą░ ąŠčüąĮąŠą▓ąĄ ą┐čĆąĄą┤čŗą┤čāčēąĄą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ, ąĖčüą┐ąŠą╗čīąĘčāčÅ ąĖąĮč鹥ą│čĆąĖčĆąŠą▓ą░ąĮąĖąĄ
ŌĆó ą┐čĆąĄą┤čüą║ą░ąĘčŗą▓ą░čÅ ą▒čāą┤čāčēąĄąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĮą░ ąŠčüąĮąŠą▓ąĄ ą┤ąĖčäč乥čĆąĄąĮčåąĖčĆąŠą▓ą░ąĮąĖčÅ.
ąØą░ čĆąĖčü. 2-2 ą┐ąŠą║ą░ąĘą░ąĮą░ ą▒ąŠą╗ąĄąĄ ą┐ąŠą┤čĆąŠą▒ąĮą░čÅ čüčģąĄą╝ą░ PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░, ą│ą┤ąĄ Tp, Ti, ąĖ Td ąŠą▒ąŠąĘąĮą░čćą░čÄčé ą║ąŠąĮčüčéą░ąĮčéčŗ ą▓čĆąĄą╝ąĄąĮąĖ ą┤ą╗čÅ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠą│ąŠ, ąĖąĮč鹥ą│čĆą░ą╗čīąĮąŠą│ąŠ ąĖ ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠą│ąŠ čāčüą╗ąŠą▓ąĖą╣ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ.
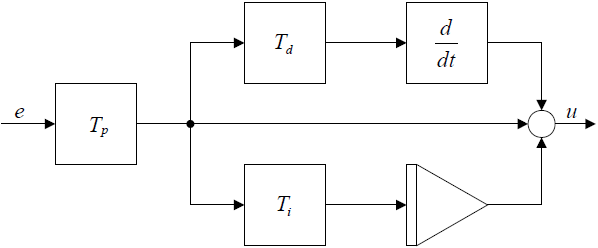
ąĀąĖčü. 2-2. ąĪčģąĄą╝ą░ ą▓ąĮčāčéčĆąĄąĮąĮąĄą│ąŠ čāčüčéčĆąŠą╣čüčéą▓ą░ PID-čĆąĄą│čāą╗čÅč鹊čĆą░.
2.1 ą¤čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮą░čÅ čüąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ PID-čĆąĄą│čāą╗čÅč鹊čĆą░
ą¤čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠąĄ čāčüą╗ąŠą▓ąĖąĄ (P) ą┐ąŠą┤ą░ąĄčé ąĮą░ ą▓čģąŠą┤ čüąĖčüč鹥ą╝čŗ ąĘąĮą░č湥ąĮąĖąĄ, ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠąĄ ąŠčłąĖą▒ą║ąĄ. ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ č鹊ą╗čīą║ąŠ P-čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą┤ą░ąĄčé ą┐ąŠčüč鹊čÅąĮąĮčāčÄ ąŠčłąĖą▒ą║čā ą▓ąŠ ą▓čüąĄčģ čüą╗čāčćą░čÅčģ ą║čĆąŠą╝ąĄ č鹥čģ, ą║ąŠą│ą┤ą░ čāą┐čĆą░ą▓ą╗čÅčÄčēąĖą╣ ą▓čģąŠą┤ čüąĖčüč鹥ą╝čŗ čĆą░ą▓ąĄąĮ 0, ąĖ ą▓čŗčģąŠą┤ąĮąŠąĄ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čĆą░ą▓ąĮąŠ čéčĆąĄą▒čāąĄą╝ąŠą╝čā. ąØą░ čĆąĖčüčāąĮą║ąĄ 2-3 čüčéą░čéąĖč湥čüą║ą░čÅ ąŠčłąĖą▒ą║ą░ ą┐ąŠčÅą▓ą╗čÅąĄčéčüčÅ ą┐ąŠčüą╗ąĄ č鹊ą│ąŠ, ą║ą░ą║ ąĖąĘą╝ąĄąĮąĖą╗ąŠčüčī čéčĆąĄą▒čāąĄą╝ąŠąĄ (ąŠą┐ąŠčĆąĮąŠąĄ, reference, ref) ąĘąĮą░č湥ąĮąĖąĄ. ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čüą╗ąĖčłą║ąŠą╝ ą▒ąŠą╗čīčłąŠą│ąŠ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ P-čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ (Tp) ą▓ PID-čĆąĄą│čāą╗čÅč鹊čĆąĄ ą┤ąĄą╗ą░ąĄčé čüąĖčüč鹥ą╝čā čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ąĮąĄčüčéą░ą▒ąĖą╗čīąĮąŠą╣.
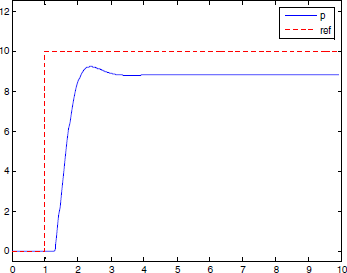
ąĀąĖčü. 2-3. ą×čéą║ą╗ąĖą║ P-čĆąĄą│čāą╗čÅč鹊čĆą░ ąĮą░ čüą║ą░čćą║ąŠąŠą▒čĆą░ąĘąĮąŠąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ąŠą┐ąŠčĆąĮąŠą│ąŠ ą┐ą░čĆą░ą╝ąĄčéčĆą░.
2.2 ąśąĮč鹥ą│čĆą░ą╗čīąĮą░čÅ čüąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ PID-čĆąĄą│čāą╗čÅč鹊čĆą░
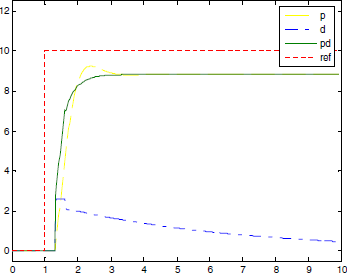
ąśąĮč鹥ą│čĆą░ą╗čīąĮąŠąĄ čāčüą╗ąŠą▓ąĖąĄ (I) ą▓čŗą┤ą░ąĄčé ąĮą░ ą▓čģąŠą┤ čüąĖčüč鹥ą╝čŗ ąĘąĮą░č湥ąĮąĖąĄ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, ąĘą░ą▓ąĖčüčÅčēąĄąĄ ąŠčé čüčāą╝ą╝čŗ ą┐čĆąĄą┤čŗą┤čāčēąĖčģ ąŠčłąĖą▒ąŠą║. ąĪčāą╝ą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ ąŠčłąĖą▒ąŠą║ ą▒čāą┤ąĄčé ą┐čĆąŠą┤ąŠą╗ąČą░čéčīčüčÅ, ą┐ąŠą║ą░ ą▓čŗčģąŠą┤ąĮąŠąĄ ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░ąĄą╝ąŠąĄ čüąĖčüč鹥ą╝ąŠą╣ ąĘąĮą░č湥ąĮąĖąĄ ąĮąĄ čüčéą░ąĮąĄčé čĆą░ą▓ąĮčŗą╝ čéčĆąĄą▒čāąĄą╝ąŠą╝čā, ąĖ ą║ąŠą│ą┤ą░ ąŠą┐ąŠčĆąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čüčéą░ą▒ąĖą╗čīąĮąŠ, č鹊 čüčéą░čéąĖč湥čüą║ą░čÅ ąŠčłąĖą▒ą║ą░ ą▒čāą┤ąĄčé ąĮčāą╗ąĄą▓ąŠą╣. ą¦ą░čēąĄ ą▓čüąĄą│ąŠ čüąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ I ąĮąŠčĆą╝ą░ą╗čīąĮąŠ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą▓ą╝ąĄčüč鹥 čü čüąŠčüčéą░ą▓ą╗čÅčÄčēąĄą╣ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ P, ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 č湥ą│ąŠ ą┐ąŠą╗čāčćą░ąĄčéčüčÅ PI-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ. ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ č鹊ą╗čīą║ąŠ I-čüąŠčüčéą░ą▓ą╗čÅčÄčēąĄą╣ ą┐čĆąĖą▓ąĄą┤ąĄčé ą║ ą╝ąĄą┤ą╗ąĄąĮąĮąŠą╝čā čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÄ ąĖ čćą░čüč鹊 ą║ čüą░ą╝ąŠą▓ąŠąĘą▒čāąČą┤ąĄąĮąĖčÄ čüąĖčüč鹥ą╝čŗ. ąØą░ čĆąĖčü. 2-4 ą┐ąŠą║ą░ąĘą░ąĮčŗ ąŠčéą║ą╗ąĖą║ąĖ čüąĖčüč鹥ą╝čŗ čü ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄą╝ I ąĖ PI čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ. ąÜą░ą║ ą╝ąŠąČąĮąŠ ą▓ąĖą┤ąĄčéčī, ąŠčéą║ą╗ąĖą║ PI-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ąĮąĄ ąĖą╝ąĄąĄčé čüčéą░čéąĖč湥čüą║ąŠą╣ ąŠčłąĖą▒ą║ąĖ, ąĖ ąŠčéą║ą╗ąĖą║ I-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ąŠč湥ąĮčī ą╝ąĄą┤ą╗ąĄąĮąĮčŗą╣.
ąĀąĖčü. 2-4. ą×čéą║ą╗ąĖą║ I- ąĖ PI-čĆąĄą│čāą╗čÅč鹊čĆąŠą▓ ąĮą░ čüą║ą░čćą║ąŠąŠą▒čĆą░ąĘąĮąŠąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ąŠą┐ąŠčĆąĮąŠą│ąŠ ą┐ą░čĆą░ą╝ąĄčéčĆą░.
2.3 ąöąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮą░čÅ čüąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ PID-čĆąĄą│čāą╗čÅč鹊čĆą░
ąöąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠąĄ čāčüą╗ąŠą▓ąĖąĄ (D) ą┤ąŠą▒ą░ą▓ą╗čÅąĄčé ą║ ą▓čģąŠą┤ąĮąŠą╝čā čüąĖą│ąĮą░ą╗čā čüąĖčüč鹥ą╝čŗ (u) ąĖąĮč乊čĆą╝ą░čåąĖčÄ ąŠ čüą║ąŠčĆąŠčüčéąĖ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅ ąŠą┐ąŠčĆąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ (ąĮą░čüą║ąŠą╗čīą║ąŠ ą▒čŗčüčéčĆąŠ ąĖąĘą╝ąĄąĮčÅąĄčéčüčÅ ąŠčłąĖą▒ą║ą░ e). ąŁč鹊 čāą╗čāčćčłą░ąĄčé ąŠčéą║ą╗ąĖą║ ąĮą░ ą▒čŗčüčéčĆąŠąĄ čüą╗čāčćą░ą╣ąĮąŠąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ą▓ čüąŠčüč鹊čÅąĮąĖąĖ čüąĖčüč鹥ą╝čŗ ąĖą╗ąĖ ą▓ ąŠą┐ąŠčĆąĮąŠą╝ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠą╝ ąĘąĮą░č湥ąĮąĖąĖ. ąĪąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ D ąŠą▒čŗčćąĮąŠ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ čüąŠą▓ą╝ąĄčüčéąĮąŠ čü P ąĖą╗ąĖ PI, ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 č湥ą│ąŠ ą┐ąŠą╗čāčćą░čÄčéčüčÅ PD- ąĖą╗ąĖ PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ. ąĪą╗ąĖčłą║ąŠą╝ ą▒ąŠą╗čīčłą░čÅ čüąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ D ąŠą▒čŗčćąĮąŠ ą┐čĆąĖą▓ąŠą┤ąĖčé ą║ ąĮąĄčüčéą░ą▒ąĖą╗čīąĮąŠčüčéąĖ čüąĖčüč鹥ą╝čŗ. ąĀąĖčü. 2-5 ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čĆąĄąĘčāą╗čīčéą░čéčŗ čĆą░ą▒ąŠčéčŗ D-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ąĖ PD-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░. ą×čéą▓ąĄčé ąŠčé PD-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ą┤ą░ąĄčé čāčüą║ąŠčĆąĄąĮąĮąŠąĄ ą▓ąŠąĘčĆą░čüčéą░ąĮąĖąĄ ąŠą▒čĆą░ą▒ą░čéčŗą▓ą░ąĄą╝ąŠą│ąŠ čüąĖčüč鹥ą╝ąŠą╣ ąĘąĮą░č湥ąĮąĖčÅ ą┐ąŠ čüčĆą░ą▓ąĮąĄąĮąĖčÄ čü P-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą╝. ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 D-čüąŠčüčéą░ą▓ą╗čÅčÄčēą░čÅ ą┐ąŠ čüčāčéąĖ čĆą░ą▒ąŠčéą░ąĄčé ą║ą░ą║ čäąĖą╗čīčéčĆ ą▓čŗčüąŠą║ąŠą╣ čćą░čüč鹊čéčŗ (ążąÆą¦), čüč鹊čÅčēąĖą╣ ąĮą░ čüąĖą│ąĮą░ą╗ąĄ ąŠčłąĖą▒ą║ąĖ, ąĖ čŹč鹊čé čäą░ą║čé ąŠč湥ąĮčī ą┐čĆąŠčüč鹊 ą╝ąŠąČąĄčé ą┐čĆąĖą▓ąĄčüčéąĖ ą║ ąĮąĄčüčéą░ą▒ąĖą╗čīąĮąŠčüčéąĖ čüąĖčüč鹥ą╝čŗ ąĖ ą┤ąĄą╗ą░ąĄčé ąĄčæ ą▒ąŠą╗ąĄąĄ čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠą╣ ą║ čłčāą╝čā ąĖ ą┐ąŠą╝ąĄčģą░ą╝.
ąĀąĖčü. 2-5. ą×čéą║ą╗ąĖą║ D- ąĖ PD-čĆąĄą│čāą╗čÅč鹊čĆąŠą▓ ąĮą░ čüą║ą░čćą║ąŠąŠą▒čĆą░ąĘąĮąŠąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ąŠą┐ąŠčĆąĮąŠą│ąŠ ą┐ą░čĆą░ą╝ąĄčéčĆą░.
ąĢčüą╗ąĖ ąŠą▒čŖąĄą┤ąĖąĮąĖčéčī ą▓čüąĄ čéčĆąĖ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖąĄ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, č鹊 ą┐ąŠą╗čāčćąĖčéčüčÅ PID-ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ, ą║ąŠč鹊čĆčŗą╣ ąŠą▒čŗčćąĮąŠ ą┤ą░ąĄčé ąĮą░ąĖą╗čāčćčłąĖąĄ čĆąĄąĘčāą╗čīčéą░čéčŗ ą▓ čāą┐čĆą░ą▓ą╗ąĄąĮąĖąĖ. ąĀąĖčü. 1-1 čüčĆą░ą▓ąĮąĖą▓ą░ąĄčé ą╝ąĄąČą┤čā čüąŠą▒ąŠą╣ ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆčŗ P, PI ąĖ PID. PI čāą╗čāčćčłą░ąĄčé P čāą┤ą░ą╗ąĄąĮąĖąĄą╝ čüčéą░čéąĖč湥čüą║ąŠą╣ ąŠčłąĖą▒ą║ąĖ, ąĖ PID čāą╗čāčćčłą░ąĄčé PI čāčüą║ąŠčĆąĄąĮąĖąĄą╝ ąŠčéą▓ąĄčéą░ ąĖ ąŠčéčüčāčéčüčéą▓ąĖąĄą╝ ą┐čĆąĖ čŹč鹊ą╝ ą┐ąĄčĆąĄčĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ.
2.4 ąØą░čüčéčĆąŠą╣ą║ą░ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ PID-čĆąĄą│čāą╗čÅč鹊čĆą░
ąĪą░ą╝čŗą╣ ą╗čāčćčłąĖą╣ čüą┐ąŠčüąŠą▒ ąĮą░ą╣čéąĖ ąĮčāąČąĮčŗąĄ ą┐ą░čĆą░ą╝ąĄčéčĆčŗ PID - ą┐ąŠą╗čāčćąĖčéčī ąĖčģ ąĖąĘ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąŠą╣ ą╝ąŠą┤ąĄą╗ąĖ čüąĖčüč鹥ą╝čŗ, ą┐ą░čĆą░ą╝ąĄčéčĆčŗ ą╝ąŠą│čāčé ą▒čŗčéčī ą▓čŗčćąĖčüą╗ąĄąĮčŗ ą┐ąŠ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠą╝čā ąŠčéą║ą╗ąĖą║čā čüąĖčüč鹥ą╝čŗ. ą¦ą░čüč鹊 ą┐ąŠą╗ąĮąŠąĄ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąŠąĄ ąŠą┐ąĖčüą░ąĮąĖąĄ čüąĖčüč鹥ą╝čŗ ąŠčéčüčāčéčüčéą▓čāąĄčé, ąĖ ą┐čĆąĖčģąŠą┤ąĖčéčüčÅ čŹą║čüą┐ąĄčĆąĖą╝ąĄąĮčéą░ą╗čīąĮąŠ ą┐ąŠą┤ą▒ąĖčĆą░čéčī ą┐ą░čĆą░ą╝ąĄčéčĆčŗ PID-čĆąĄą│čāą╗čÅč鹊čĆą░. ąØą░čģąŠąČą┤ąĄąĮąĖąĄ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ PID-čĆąĄą│čāą╗čÅč鹊čĆą░ ą╝ąŠąČąĄčé ą▒čŗčéčī čüą╗ąŠąČąĮąŠą╣ ąĘą░ą┤ą░č湥ą╣. ąÆą░ąČąĮąŠ čģąŠčĆąŠčłąŠ ąĘąĮą░čéčī čüąĖčüč鹥ą╝čā ąĖ ąĄčæ ą┐ąŠą▓ąĄą┤ąĄąĮąĖąĄ ą▓ čĆą░ąĘą╗ąĖčćąĮčŗčģ čāčüą╗ąŠą▓ąĖčÅčģ. ą×ą┐čéąĖą╝ą░ą╗čīąĮąŠąĄ ą┐ąŠą▓ąĄą┤ąĄąĮąĖąĄ ą▓ ąŠčéą▓ąĄčé ąĮą░ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ čāčüą╗ąŠą▓ąĖą╣ ąĖą╗ąĖ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ąŠą┐ąŠčĆąĮąŠą╣ ąĘą░ą┤ą░ąĮąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ ąĘą░ą▓ąĖčüąĖčé ąŠčé ą║ąŠąĮą║čĆąĄčéąĮąŠą│ąŠ ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ. ąØąĄą║ąŠč鹊čĆčŗąĄ ą┐čĆąŠčåąĄčüčüčŗ ąĮąĄ ą┤ąŠą╗ąČąĮčŗ ą┤ąŠą┐čāčüą║ą░čéčī ą┐ąĄčĆąĄčĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ (ą▓čŗą▒čĆąŠčüąŠą▓) ą▓ ąŠčéą▓ąĄčé ąĮą░ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ ą▓čģąŠą┤ąĮąŠą╣ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ. ąöčĆčāą│ąĖąĄ ą┐čĆąŠčåąĄčüčüčŗ ą┤ąŠą╗ąČąĮčŗ ą╝ąĖąĮąĖą╝ąĖąĘąĖčĆąŠą▓ą░čéčī čĆą░čüčģąŠą┤ 菹ĮąĄčĆą│ąĖąĖ ąĮą░ ą┐čāčéąĖ ą┤ąŠčüčéąĖąČąĄąĮąĖčÅ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ. ąś ą┐ąŠčćčéąĖ ą▓čüąĄą│ą┤ą░ ą│ą╗ą░ą▓ąĮčŗą╝ čéčĆąĄą▒ąŠą▓ą░ąĮąĖąĄą╝ čÅą▓ą╗čÅąĄčéčüčÅ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéčī čüąĖčüč鹥ą╝čŗ. ą¤čĆąŠčåąĄčüčü čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ąĮąĄ ą┤ąŠą╗ąČąĄąĮ ą┤ąŠą┐čāčüą║ą░čéčī čüą░ą╝ąŠą▓ąŠąĘą▒čāąČą┤ąĄąĮąĖčÅ ą┤ą╗čÅ ą╗čÄą▒ąŠą│ąŠ ą▓ą░čĆąĖą░ąĮčéą░ č鹥ą║čāčēąĖčģ čāčüą╗ąŠą▓ąĖą╣ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĖą╗ąĖ ą╗čÄą▒čŗąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅ ą▓čģąŠą┤ąĮąŠą╣ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ. ąÜčĆąŠą╝ąĄ č鹊ą│ąŠ, čŹčäč乥ą║čé čüčéą░ą▒ąĖą╗ąĖąĘą░čåąĖąĖ ą┤ąŠą╗ąČąĄąĮ čāą║ą╗ą░ą┤čŗą▓ą░čéčīčüčÅ ą▓ ąĘą░čĆą░ąĮąĄąĄ ąĘą░ą┤ą░ąĮąĮčŗąĄ ąŠą│čĆą░ąĮąĖč湥ąĮąĖčÅ ą┐ąŠ ą▓čĆąĄą╝ąĄąĮąĖ.
ąĢčüčéčī ąĮąĄčüą║ąŠą╗čīą║ąŠ ą╝ąĄč鹊ą┤ąŠą▓ ą┤ą╗čÅ ąĮą░čüčéčĆąŠą╣ą║ąĖ ą┐ąĄčéą╗ąĖ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ PID. ąÆčŗą▒ąŠčĆ ą╝ąĄč鹊ą┤ą░ ąĘą░ą▓ąĖčüąĖčé ąŠčé č鹊ą│ąŠ, ą╝ąŠąČąĄčé ą╗ąĖ ą┐čĆąŠčåąĄčüčü čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▒čŗčéčī ąŠčéą║ą╗čÄč湥ąĮąĮčŗą╝ ą┤ą╗čÅ ąĮą░čüčéčĆąŠą╣ą║ąĖ, ąĖą╗ąĖ ąĮąĄčé. ą£ąĄč鹊ą┤ Ziegler-Nichols čģąŠčĆąŠčłąŠ ąĖąĘą▓ąĄčüč鹥ąĮ ą║ą░ą║ čüčéčĆą░č鹥ą│ąĖčÅ ąĮą░čüčéčĆąŠą╣ą║ąĖ, ąĮąĄ čéčĆąĄą▒čāčÄčēą░čÅ ąŠčéą║ą╗čÄč湥ąĮąĖčÅ čüąĖčüč鹥ą╝čŗ. ąØą░ ą┐ąĄčĆą▓ąŠą╝ čłą░ą│ąĄ čŹč鹊ą╣ ą╝ąĄč鹊ą┤ąĖą║ąĖ čāčüčéą░ąĮą░ą▓ą╗ąĖą▓ą░čÄčé čāčüąĖą╗ąĄąĮąĖąĄ I ąĖ D čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ ą▓ 0, čāą▓ąĄą╗ąĖčćąĖą▓ą░čÄčé čāčüąĖą╗ąĄąĮąĖąĄ P, ą┐ąŠą║ą░ ąĮąĄ ą▓čŗčģąŠą┤ąĄ ąĮąĄ ą▒čāą┤čāčé ą┐ąŠą╗čāč湥ąĮčŗ čāčüčéą░ąĮąŠą▓ąĖą▓čłąĖąĄčüčÅ ąĖ čüčéą░ą▒ąĖą╗čīąĮčŗąĄ ą║ąŠą╗ąĄą▒ą░ąĮąĖčÅ (ą┐čĆąĖ čŹč鹊ą╝ ą▓čŗčģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗ ą┤ąŠą╗ąČąĄąĮ ą║ą░ą║ ą╝ąŠąČąĮąŠ ą╝ąĄąĮčīčłąĄ ąŠčéą╗ąĖčćą░čéčīčüčÅ ąŠčé ąŠą┐ąŠčĆąĮąŠą│ąŠ). ąŚą░č鹥ą╝ ąĘą░ą┐ąĖčüčŗą▓ą░čÄčé ą║čĆąĖčéąĖč湥čüą║ąŠąĄ čāčüąĖą╗ąĄąĮąĖąĄ Kc ąĖ ą┐ąĄčĆąĖąŠą┤ ą│ąĄąĮąĄčĆą░čåąĖąĖ Pc, ąĖ ąĘąĮą░č湥ąĮąĖčÅ P, I ąĖ D ą┐ąŠą┤čüčéčĆą░ąĖą▓ą░čÄčéčüčÅ ą┐ąŠ čéą░ą▒ą╗ąĖčåąĄ 2-1.
ąóą░ą▒ą╗ąĖčåą░ 2-1. ą¤ą░čĆą░ą╝ąĄčéčĆčŗ ą╝ąĄč鹊ą┤ąĖą║ąĖ Ziegler-Nichols ą┤ą╗čÅ ąĮą░čüčéčĆąŠą╣ą║ąĖ PID.
| ą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆ |
Kp |
Ti |
Td |
| P |
0.5 * Kc |
|
|
| PD |
0.65 * Kc |
|
0.12 * Pc |
| PI |
0.45 * Kc |
0.85 * Pc |
|
| PID |
0.65 * Kc |
0.5 * Pc |
0.12 * Pc |
ąöą░ą╗čīąĮąĄą╣čłą░čÅ ąĮą░čüčéčĆąŠą╣ą║ą░ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ čćą░čüč鹊 ąĮčāąČąĮą░ ą┤ą╗čÅ ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĖ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ PID-čĆąĄą│čāą╗čÅč鹊čĆą░.
ąØąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ąĖą╝ąĄčéčī ą▓ ą▓ąĖą┤čā, čćč鹊 ąĄčüčéčī čüąĖčüč鹥ą╝čŗ, ą┤ą╗čÅ ą║ąŠč鹊čĆčŗčģ PID-čĆąĄą│čāą╗čÅč鹊čĆ ąĮąĄ ąŠč湥ąĮčī čģąŠčĆąŠčł, ąĖą╗ąĖ čüąĖčüč鹥ą╝čŗ, ą│ą┤ąĄ ąŠąĮ ą▒čāą┤ąĄčé ąĮąŠčĆą╝ą░ą╗čīąĮąŠ čĆą░ą▒ąŠčéą░čéčī č鹊ą╗čīą║ąŠ ą▓ ą╝ą░ą╗ąŠą╝ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ąĖą╝ąĄčÄčēąĖčģčüčÅ čüąŠčüč鹊čÅąĮąĖą╣ čüąĖčüč鹥ą╝čŗ. ąŁč鹊 ąĮąĄą╗ąĖąĮąĄą╣ąĮčŗąĄ čüąĖčüč鹥ą╝čŗ, ąĮąŠ ąŠčüąĮąŠą▓ąĮą░čÅ ą┐čĆąŠą▒ą╗ąĄą╝ą░ čü PID-čĆąĄą│čāą╗čÅč鹊čĆąŠą╝ ą┐čĆąŠčÅą▓ą╗čÅąĄčéčüčÅ čü ąĮąĄčüčéą░ą▒ąĖą╗čīąĮčŗą╝ąĖ čüąĖčüč鹥ą╝ą░ą╝ąĖ, ąĖ ą║ąŠą│ą┤ą░ čŹčäč乥ą║čé ąŠčé ą▓čģąŠą┤ąĮąŠą│ąŠ ą▓ąŠąĘą┤ąĄą╣čüčéą▓ąĖčÅ ąĘą░ą▓ąĖčüąĖčé ąŠčé čüąŠčüč鹊čÅąĮąĖčÅ čüąĖčüč鹥ą╝čŗ.
2.5 ąöąĖčüą║čĆąĄčéąĮčŗą╣ PID-čĆąĄą│čāą╗čÅč鹊čĆ
ąöąĖčüą║čĆąĄčéąĮčŗą╣ (čåąĖčäčĆąŠą▓ąŠą╣) PID-čĆąĄą│čāą╗čÅč鹊čĆ ą▒čāą┤ąĄčé čćąĖčéą░čéčī ąŠčłąĖą▒ą║čā, ą┤ąĄą╗ą░čéčī ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ąĖ ą▓čŗą┤ą░ą▓ą░čéčī ą▓čŗčģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čü ąĘą░ą┤ą░ąĮąĮčŗą╝ąĖ ąĖąĮč鹥čĆą▓ą░ą╗ą░ą╝ąĖ ą▓čĆąĄą╝ąĄąĮąĖ, čü ą┐ąĄčĆąĖąŠą┤ąŠą╝ ą▓čŗą▒ąŠčĆą║ąĖ T. ąÆčĆąĄą╝čÅ ą▓čŗą▒ąŠčĆą║ąĖ T ą┤ąŠą╗ąČąĮąŠ ą▒čŗčéčī ą│ą░čĆą░ąĮčéąĖčĆąŠą▓ą░ąĮąĮąŠ ą╝ąĄąĮčīčłąĄ, č湥ą╝ čüą░ą╝čŗą╣ ą╝ą░ą╗ąĄąĮčīą║ąĖą╣ ąĖąĮč鹥čĆą▓ą░ą╗ ą▓čĆąĄą╝ąĄąĮąĖ, ą║ąŠč鹊čĆčŗą╣ ą╝ąŠąČąĄčé ąĖą╝ąĄčéčī ą▓ čüąĖčüč鹥ą╝ąĄ (ą┐ąŠ č鹥čģąĘą░ą┤ą░ąĮąĖčÄ) ą▓ą░ąČąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ.
2.5.1 ą×čüąĮąŠą▓ą░ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ PID-čĆąĄą│čāą╗čÅč鹊čĆą░
ąÆ ąŠčéą╗ąĖčćąĖąĄ ąŠčé ą┐čĆąŠčüčéčŗčģ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, PID-čĆąĄą│čāą╗čÅč鹊čĆ ą╝ąŠąČąĄčé ą╝ą░ąĮąĖą┐čāą╗ąĖčĆąŠą▓ą░čéčī čāą┐čĆą░ą▓ą╗čÅčÄčēąĖą╝ čüąĖą│ąĮą░ą╗ąŠą╝, ąŠčüąĮąŠą▓čŗą▓ą░čÅčüčī ąĮą░ ąĖčüč鹊čĆąĖąĖ ąĖ čüą║ąŠčĆąŠčüčéąĖ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░. ąŁč鹊 ą┤ą░ąĄčé ą╝ąĄč鹊ą┤ ą▒ąŠą╗ąĄąĄ č鹊čćąĮąŠą│ąŠ ąĖ čüčéą░ą▒ąĖą╗čīąĮąŠą│ąŠ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ.
ąØą░ čĆąĖčü. 2-2 ą┐ąŠą║ą░ąĘą░ąĮą░ čüčģąĄą╝ą░ PID-čĆąĄą│čāą╗čÅč鹊čĆą░, ą│ą┤ąĄ Tp, Ti ąĖ Tp ąŠą▒ąŠąĘąĮą░čćą░čÄčé ą║ąŠąĮčüčéą░ąĮčéčŗ ą▓čĆąĄą╝ąĄąĮąĖ ą┤ą╗čÅ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠą│ąŠ, ąĖąĮč鹥ą│čĆą░ą╗čīąĮąŠą│ąŠ ąĖ ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠą│ąŠ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ.
ą¤ąĄčĆąĄą┤ą░č鹊čćąĮą░čÅ čäčāąĮą║čåąĖčÅ čüąĖčüč鹥ą╝čŗ ąĮą░ čĆąĖčü. 2-2:
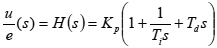
ąŁč鹊 ą┤ą░ąĄčé ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī u ąŠčé e ą┐ąŠ ąŠčüąĖ ą▓čĆąĄą╝ąĄąĮąĖ:
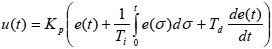
ąÉą┐ą┐čĆąŠą║čüąĖą╝ą░čåąĖčÅ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ I ąĖ D:
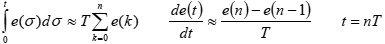
ąŚą┤ąĄčüčī n - ą┤ąĖčüą║čĆąĄčéąĮčŗą╣ čłą░ą│ ą▓čĆąĄą╝ąĄąĮąĖ t. ąŁč鹊 ą┤ą░ąĄčé ą▓čŗčĆą░ąČąĄąĮąĖąĄ ą┤ą╗čÅ čĆąĄą│čāą╗čÅč鹊čĆą░:
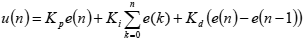
ąŚą┤ąĄčüčī:
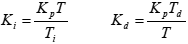
ą¦č鹊ą▒čŗ ąĖąĘą▒ąĄąČą░čéčī ąĖąĘą╝ąĄąĮąĄąĮąĖą╣ ą▓ čéčĆąĄą▒čāąĄą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮąĄ ą┐čĆąŠčåąĄčüčüą░ ąĖ ą╗čÄą▒čŗčģ ąĮąĄąČąĄą╗ą░č鹥ą╗čīąĮčŗčģ ą▒čŗčüčéčĆčŗčģ ąĖąĘą╝ąĄąĮąĄąĮąĖą╣ ą▓ čāą┐čĆą░ą▓ą╗čÅčÄčēąĄą╝ čüąĖą│ąĮą░ą╗ąĄ, čĆąĄą│čāą╗čÅč鹊čĆ čāą╗čāčćčłąĄąĮ ąĮą░ ą▒ą░ąĘąĄ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĄą╣ D č鹊ą╗čīą║ąŠ ąĮą░ ąĘąĮą░č湥ąĮąĖąĖ ą▓ąĄą╗ąĖčćąĖąĮčŗ ą┐čĆąŠčåąĄčüčüą░:
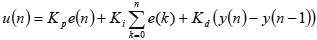
[3 ąĀąĄą░ą╗ąĖąĘą░čåąĖčÅ PID-čĆąĄą│čāą╗čÅč鹊čĆą░]
ąŁč鹊čé ą░ą┐ąĮąŠčāčé ą┐ąŠčüčéą░ą▓ą╗čÅąĄčéčüčÅ čü ą│ąŠč鹊ą▓ąŠą╣ čĆąĄą░ą╗ąĖąĘą░čåąĖąĄą╣ PID-čĆąĄą│čāą╗čÅč鹊čĆą░ ąĮą░ čÅąĘčŗą║ąĄ C [2]. ą¤ąŠą╗ąĮčāčÄ ą┤ąŠą║čāą╝ąĄąĮčéą░čåąĖčÄ ą┐ąŠ ąĖčüčģąŠą┤ąĮąŠą╝čā ą║ąŠą┤čā ą╝ąŠąČąĮąŠ ąĮą░ą╣čéąĖ, ąĄčüą╗ąĖ ąŠčéą║čĆčŗčéčī čäą░ą╣ą╗ readme.html, ą║ąŠč鹊čĆčŗą╣ ąĖą╝ąĄąĄčéčüčÅ ą▓ ą┐ą░ą║ąĄč鹥 ą░čĆčģąĖą▓ą░.
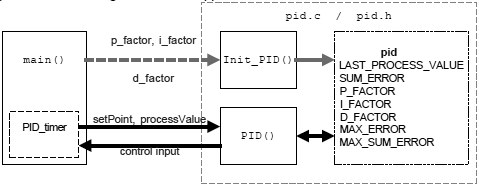
ąĀąĖčü. 3-1. ąæą╗ąŠą║-čüčģąĄą╝ą░ ą┤ąĄą╝ąŠąĮčüčéčĆą░čåąĖąŠąĮąĮąŠą│ąŠ ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ PID-čĆąĄą│čāą╗čÅč鹊čĆą░.
ąØą░ čĆąĖčü. 3-1 ą┐ąŠą║ą░ąĘą░ąĮą░ čāą┐čĆąŠčēąĄąĮąĮą░čÅ čüčģąĄą╝ą░ ą┤ąĄą╝ąŠ-ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ [2]. PID-čĆąĄą│čāą╗čÅč鹊čĆ ąĖčüą┐ąŠą╗čīąĘčāąĄčé čüčéčĆčāą║čéčāčĆčā (struct) ą┤ą╗čÅ čüąŠčģčĆą░ąĮąĄąĮąĖčÅ čüą▓ąŠąĄą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ ąĖ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓. ąŁčéą░ čüčéčĆčāą║čéčāčĆą░ ąĖąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆčāąĄčéčüčÅ ą▓ č鹥ą╗ąĄ čäčāąĮą║čåąĖąĖ main, ąĖ čäčāąĮą║čåąĖčÅą╝ Init_PID() ąĖ PID() ą┐ąĄčĆąĄą┤ą░ąĄčéčüčÅ č鹊ą╗čīą║ąŠ čāą║ą░ąĘą░č鹥ą╗čī ąĮą░ čüčéčĆčāą║čéčāčĆčā.
ążčāąĮą║čåąĖčÅ PID() ą┤ąŠą╗ąČąĮą░ ą▒čŗčéčī ą▓čŗąĘą▓ą░ąĮą░ ąĮą░ ą║ą░ąČą┤ąŠą╝ ąĖąĮč鹥čĆą▓ą░ą╗ąĄ ą▓čĆąĄą╝ąĄąĮąĖ T. ąŁč鹊 čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąŠ čü ą┐ąŠą╝ąŠčēčīčÄ čéą░ą╣ą╝ąĄčĆą░, ą║ąŠč鹊čĆčŗą╣ čāčüčéą░ąĮą░ą▓ą╗ąĖą▓ą░ąĄčé čäą╗ą░ą│ PID_timer, ą║ąŠą│ą┤ą░ ą┐čĆąŠčģąŠą┤ąĖčé ąĖąĮč鹥čĆą▓ą░ą╗ ą▓čĆąĄą╝ąĄąĮąĖ T. ąÜąŠą│ą┤ą░ čäą╗ą░ą│ PID_timer čāčüčéą░ąĮąŠą▓ą╗ąĄąĮ, ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝ą░ ą▓ čåąĖą║ą╗ąĄ main čćąĖčéą░ąĄčé čéčĆąĄą▒čāąĄą╝ąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ą┐čĆąŠčåąĄčüčüą░ (ąŠą┐ąŠčĆąĮąŠąĄ ąŠčéčüą╗ąĄąČąĖą▓ą░ąĄą╝ąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ setPoint) ąĖ č鹥ą║čāčēąĄąĄ ąĘąĮą░č湥ąĮąĖąĄ ą┐čĆąŠčåąĄčüčüą░ čüąĖčüč鹥ą╝čŗ, ą▓čŗąĘčŗą▓ą░ąĄčéčüčÅ PID(), ąĖ ą▓čŗą▓ąŠą┤ąĖčé čĆąĄąĘčāą╗čīčéą░čé ąĮą░ čāą┐čĆą░ą▓ą╗čÅčÄčēąĖą╣ ą▓čģąŠą┤.
ą¦č鹊ą▒čŗ čāą▓ąĄą╗ąĖčćąĖčéčī č鹊čćąĮąŠčüčéčī, ą╝ąĮąŠąČąĖč鹥ą╗ąĖ p_factor, i_factor ąĖ d_factor čüą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮčŗ čü ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą╝ 1:128. ąĀąĄąĘčāą╗čīčéą░čé ą░ą╗ą│ąŠčĆąĖčéą╝ą░ PID ąĘą░č鹥ą╝ ą╝ą░čüčłčéą░ą▒ąĖčĆčāąĄčéčüčÅ ąŠą▒čĆą░čéąĮąŠ ą┤ąĄą╗ąĄąĮąĖąĄą╝ ąĮą░ 128. ą¦ąĖčüą╗ąŠ 128 ą▓čŗą▒čĆą░ąĮąŠ ą┤ą╗čÅ č鹊ą│ąŠ, čćč鹊ą▒čŗ ąĘą░ą┤ąĄą╣čüčéą▓ąŠą▓ą░čéčī ąŠą┐čéąĖą╝ąĖąĘą░čåąĖčÄ ą║ąŠą╝ą┐ąĖą╗čÅč鹊čĆą░ (čāą╝ąĮąŠąČąĄąĮąĖąĄ ąĮą░ 128 ąĘą░ą╝ąĄąĮčÅąĄčéčüčÅ čüą┤ą▓ąĖą│ąŠą╝ ąĮą░ 1 ą▒ąĖčé ą╝ą╗ą░ą┤čłąĄą│ąŠ ą▒ą░ą╣čéą░ ąĖ ą║ąŠą┐ąĖčĆąŠą▓ą░ąĮąĖąĄą╝ čĆąĄąĘčāą╗čīčéą░čéą░ ą▓ čüčéą░čĆčłąĖą╣ ą▒ą░ą╣čé).
ąÆ ą┤ą░ą╗čīąĮąĄą╣čłąĄą╝ čŹčäč乥ą║čé ąŠčé ą╝ąĮąŠąČąĖč鹥ą╗ąĄą╣ IFactor ąĖ DFactor ą▒čāą┤čāčé ąĘą░ą▓ąĖčüąĄčéčī ąŠčé ąĖąĮč鹥čĆą▓ą░ą╗ą░ ą▓čŗą▒ąŠčĆą║ąĖ T.
T
IFactor = 128 * Kp * ---
Ti
Td
DFactor = 128 * Kp * ---
T
3.1 ąĪą▓ąĄčĆčéą║ą░ ą┤ą╗čÅ ąĖąĮč鹥ą│čĆą░ą╗ą░
ąÆčģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ u ąĖąĮąŠą│ą┤ą░ ą┤ąŠčüčéąĖą│ą░ąĄčé ąĮąĄą║ąŠč鹊čĆąŠą│ąŠ ą┐čĆąĄą┤ąĄą╗ą░. ą¤čĆąĄą┤ąĄą╗ čüą▓čÅąĘą░ąĮ ą╗ąĖą▒ąŠ čü ąŠą│čĆą░ąĮąĖč湥ąĮąĮčŗą╝ čćąĖčüą╗ąŠą▓čŗą╝ ą┤ąĖą░ą┐ą░ąĘąŠąĮąŠą╝ ą┐ąĄčĆąĄą╝ąĄąĮąĮčŗčģ PID-čĆąĄą│čāą╗čÅč鹊čĆą░ (ą▓ ą║ąŠą┤ąĄ ą╝ąŠą│čāčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄąĮąĮčŗąĄ ąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ), ą╗ąĖą▒ąŠ čü ą▓čŗčģąŠą┤ąĮčŗą╝ ą┤ąĖą░ą┐ą░ąĘąŠąĮąŠą╝ čĆąĄą│čāą╗čÅč鹊čĆą░, ą╗ąĖą▒ąŠ ąĮą░čüčŗčēąĄąĮąĖąĄą╝ (ąŠą│čĆą░ąĮąĖč湥ąĮąĖąĄą╝ čüąĖą│ąĮą░ą╗ą░) ą▓ čāčüąĖą╗ąĖč鹥ą╗čÅčģ, ą╗ąĖą▒ąŠ čü ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅą╝ąĖ ą▓ ą░ą╗ą│ąŠčĆąĖčéą╝ąĄ. ąŁč鹊 ą┐čĆąŠąĖąĘąŠą╣ą┤ąĄčé, ąĄčüą╗ąĖ ąĖą╝ąĄąĄčéčüčÅ čüą╗ąĖčłą║ąŠą╝ ą▒ąŠą╗čīčłąŠąĄ čĆą░ąĘą╗ąĖčćąĖąĄ ą╝ąĄąČą┤čā ąĖąĘą╝ąĄčĆąĄąĮąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮąŠą╣ ąĖ ąŠą┐ąŠčĆąĮčŗą╝ čüąĖą│ąĮą░ą╗ąŠą╝. ą¤čĆąĖčćąĖąĮą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ą▓ ą▒ąŠą╗čīčłąĖčģ ą▓ąŠąĘą╝čāčēąĄąĮąĖčÅčģ / ą┐ąĄčĆąĄą│čĆčāąĘą║ąĄ, ą║ąŠč鹊čĆčŗąĄ čüąĖčüč鹥ą╝ą░ ą┤ąŠą╗ąČąĮą░ ąŠą▒čĆą░ą▒ąŠčéą░čéčī.
ąĢčüą╗ąĖ čĆąĄą│čāą╗čÅč鹊čĆ ąĖčüą┐ąŠą╗čīąĘčāąĄčé čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮčŗąĄ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖąĄ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ, čüąĖčéčāą░čåąĖčÅ ą╝ąŠąČąĄčé čüčéą░čéčī ą┐čĆąŠą▒ą╗ąĄą╝ą░čéąĖčćąĮąŠą╣. ąśąĮč鹥ą│čĆą░ą╗ ą┐ąŠ čüčāčéąĖ ą┐čĆąŠčüč鹊 čüčāą╝ą╝ą░ ą┐čĆąĄą┤čŗą┤čāčēąĖčģ ąĘąĮą░č湥ąĮąĖą╣, ą║ąŠč鹊čĆą░čÅ ą╝ąŠąČąĄčé ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĖčéčīčüčÅ, ąĖ čĆąĄą│čāą╗čÅč鹊čĆ ą┐ąĄčĆąĄčüčéą░ąĮąĄčé čĆą░ą▒ąŠčéą░čéčī. ąĀą░ą▒ąŠčéą░ ą▓ąŠčüčüčéą░ąĮąŠą▓ąĖčéčüčÅ, ą║ąŠą│ą┤ą░ ą▒ąŠą╗čīčłąŠąĄ ą▓ąŠąĘą╝čāčēąĄąĮąĖąĄ / ąĮą░ą│čĆčāąĘą║ą░ ąĖčüč湥ąĘąĮąĄčé, ąĖ PID čüą║ąŠą╝ą┐ąĄąĮčüąĖčĆčāąĄčé čāą┐čĆą░ą▓ą╗čÅčÄčēąĖą╣ čüąĖą│ąĮą░ą╗, ą║ą░ą║ č鹊ą╗čīą║ąŠ ąĖąĮč鹥ą│čĆą░ą╗čīąĮą░čÅ čüčāą╝ą╝ą░ ą▓ąĄčĆąĮąĄčéčüčÅ ą║ ąĮąŠčĆą╝ą░ą╗čīąĮąŠą╝čā ąĘąĮą░č湥ąĮąĖčÄ.
ą¤čĆąŠą▒ą╗ąĄą╝čā čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ ą╝ąŠąČąĮąŠ ąŠą▒ąŠą╣čéąĖ ąĮąĄčüą║ąŠą╗čīą║ąĖą╝ąĖ čüą┐ąŠčüąŠą▒ą░ą╝ąĖ. ąÆ čŹč鹊ą╣ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ čüčāą╝ą╝ą░ ą▓ ąĖąĮč鹥ą│čĆą░ą╗ąĄ ąŠą│čĆą░ąĮąĖč湥ąĮą░, ąĮąŠ ąĄą╣ ąĮąĄ ą┐ąŠąĘą▓ąŠą╗ąĄąĮąŠ ą┐čĆąĄą▓čŗčüąĖčéčī ąĘąĮą░č湥ąĮąĖąĄ MAX_I_TERM. ąÜąŠčĆčĆąĄą║čéąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ MAX_I_TERM ą▒čāą┤ąĄčé ąĘą░ą▓ąĖčüąĄčéčī ąŠčé čüą░ą╝ąŠą╣ čüąĖčüč鹥ą╝čŗ ąĖ ąĖčüą┐ąŠą╗čīąĘčāąĄą╝ąŠą│ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ą▓čŗą▒ąŠčĆą║ąĖ T.
ą¤čĆąĖą╝. ą┐ąĄčĆąĄą▓ąŠą┤čćąĖą║ą░: ą┐ąŠčģąŠąČąĖąĄ ą┐čĆąŠą▒ą╗ąĄą╝čŗ ąĄčüčéčī ąĖ ą▓ ą░ą╗ą│ąŠčĆąĖčéą╝ą░čģ ą”ą×ąĪ (čåąĖčäčĆąŠą▓ą░čÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░ čüąĖą│ąĮą░ą╗ąŠą▓, DSP), ą║ąŠą│ą┤ą░ ą┐čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮą░čÅ ą░čĆąĖčäą╝ąĄčéąĖą║ą░ ą┤ą╗čÅ čāčüą║ąŠčĆąĄąĮąĖčÅ čĆą░ą▒ąŠčéčŗ [3]. ą┤čĆčāą│ąĖąĄ ą╝ąĄč鹊ą┤čŗ čāčüčéčĆą░ąĮąĄąĮąĖčÅ ą┐čĆąŠą▒ą╗ąĄą╝čŗ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ - ą┐ąŠą▓čŗčłąĄąĮąĖąĄ čĆą░ąĘčĆčÅą┤ąĮąŠčüčéąĖ ą┐ąĄčĆąĄą╝ąĄąĮąĮčŗčģ ą▓ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅčģ, ąĖ ą┤ą░ąČąĄ ą┐ąĄčĆąĄčģąŠą┤ ąĮą░ ą░čĆąĖčäą╝ąĄčéąĖą║čā čü ą┐ą╗ą░ą▓ą░čÄčēąĄą╣ ąĘą░ą┐čÅč鹊ą╣. ąÜ čüąŠąČą░ą╗ąĄąĮąĖčÄ, čŹč鹊 čćą░čüč鹊 čüą▓čÅąĘą░ąĮąŠ čü čāą▓ąĄą╗ąĖč湥ąĮąĖąĄą╝ ąŠą▒čŖąĄą╝ą░ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ ąĖ čāčüą╗ąŠąČąĮąĄąĮąĖąĄą╝ ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĖ ąĖ čĆą░ąĘčĆą░ą▒ąŠčéą║ąĖ, čéą░ą║ čćč鹊 ąĖą╝ąĄąĄčé ąŠą│čĆą░ąĮąĖč湥ąĮąĮčāčÄ ąŠą▒ą╗ą░čüčéčī ą┐čĆąĖą╝ąĄąĮąĄąĮąĖčÅ. ąÆ ą╗čÄą▒ąŠą╝ čüą╗čāčćą░ąĄ ą┤ą╗čÅ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ čüčéą░čĆą░ą╣č鹥čüčī ąĘą░ą┤ąĄą╣čüčéą▓ąŠą▓ą░čéčī ą░ą┐ą┐ą░čĆą░čéąĮčŗąĄ čĆąĄčüčāčĆčüčŗ čÅą┤čĆą░ AVR [4].
[4 ąöąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗąĄ ąĘą░ą╝ąĄčćą░ąĮąĖčÅ]
ą¤čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĮčŗą╣ PID-čĆąĄą│čāą╗čÅč鹊čĆ čÅą▓ą╗čÅąĄčéčüčÅ čāą┐čĆąŠčēąĄąĮąĮčŗą╝ ą┐čĆąĖą╝ąĄčĆąŠą╝. ąĀąĄą│čāą╗čÅč鹊čĆ ą┤ąŠą╗ąČąĄąĮ čģąŠčĆąŠčłąŠ čĆą░ą▒ąŠčéą░čéčī, ąŠą┤ąĮą░ą║ąŠ ą╝ąŠąČąĄčé ą┐ąŠčéčĆąĄą▒ąŠą▓ą░čéčīčüčÅ čāą╗čāčćčłąĄąĮąĖąĄ, čüą▓čÅąĘą░ąĮąĮčŗą╝ čü ą║ąŠąĮą║čĆąĄčéąĮčŗą╝ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄą╝ (ą║ ą┐čĆąĖą╝ąĄčĆčā, čāčüčéčĆą░ąĮąĄąĮąĖąĄ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖą╣ ąĖ/ąĖą╗ąĖ ąĮąĄč鹊čćąĮąŠčüč鹥ą╣ ą▓ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖąĖ). ą£ąŠąČąĮąŠ ą┤ąŠą▒ą░ą▓ąĖčéčī ą║ąŠčĆčĆąĄą║čåąĖčÄ (čāčüčéčĆą░ąĮąĄąĮąĖąĄ) ąĮą░čüčŗčēąĄąĮąĖčÅ ą▓ I-čüąŠčüčéą░ą▓ą╗čÅčÄčēąĄą╣ ąĘą░ čüč湥čé P-čüąŠčüčéą░ą▓ą╗čÅčÄčēąĄą╣, ąĄčüą╗ąĖ čŹč鹊 ą┐ąŠąĘą▓ąŠą╗čÅčÄčé čāčüą╗ąŠą▓ąĖčÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ čĆąĄą│čāą╗ąĖčĆčāąĄą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ.
ąÆ ą▓čŗčćąĖčüą╗ąĄąĮąĖąĄ ą╝ąĮąŠąČąĖč鹥ą╗ąĄą╣ IFactor ąĖ DFactor ą▓čĆąĄą╝čÅ ą▓čŗą▒ąŠčĆą║ąĖ T čÅą▓ą╗čÅąĄčéčüčÅ čćą░čüčéčīčÄ ą▓čŗčĆą░ąČąĄąĮąĖčÅ. ąĢčüą╗ąĖ T ą▓čŗą▒čĆą░ąĮąŠ čüą╗ąĖčłą║ąŠą╝ ą╝ą░ą╗ąĄąĮčīą║ąĖą╝, ąĖą╗ąĖ čüą┤ąĄą╗ą░ąĮąŠ ą▒ąŠą╗čīčłąĄ 1 čüąĄą║čāąĮą┤čŗ, č鹊 ą▒čāą┤ąĄčé ąĮą░čĆčāčłąĄąĮą░ č鹊čćąĮąŠčüčéčī ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą╗ąĖą▒ąŠ ą╝ąĮąŠąČąĖč鹥ą╗čÅ IFactor, ą╗ąĖą▒ąŠ ą╝ąĮąŠąČąĖč鹥ą╗čÅ DFactor. ą¤čĆąĖą╝ąĖč鹥 čĆąĄčłąĄąĮąĖąĄ ą┐ąŠ ą┤ąŠčĆą░ą▒ąŠčéą║ąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ PID ą┐čĆąĖ ą╝ą░čüčłčéą░ą▒ąĖčĆąŠą▓ą░ąĮąĖąĖ, čćč鹊ą▒čŗ čüąŠčģčĆą░ąĮąĖčéčī č鹊čćąĮąŠčüčéčī ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ I-čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖąĄą╣ (ąĖąĮč鹥ą│čĆą░ą╗) ąĖ D-čüąŠčüčéą░ą▓ą╗čÅčÄčēąĄą╣ (ą┐čĆąŠąĖąĘą▓ąŠą┤ąĮą░čÅ).
[ąĪčüčŗą╗ą║ąĖ]
1. AVR221: Discrete PID controller on tinyAVR and megaAVR devices site:atmel.com.
2. AVR221.zip.
3. AVR223: Digital Filters with AVR (čåąĖčäčĆąŠą▓čŗąĄ čäąĖą╗čīčéčĆčŗ ąĮą░ AVR).
4. AVR201: ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ AVR. |

ąÜąŠą╝ą╝ąĄąĮčéą░čĆąĖąĖ
microsin: ąĘąĮą░č湥ąĮąĖąĄ čā ąÆą░čü 16-ą▒ąĖčéąĮąŠąĄ. ąöą╗čÅ č鹊ą│ąŠ, čćč鹊ą▒čŗ ą┐čĆąĄą▓čĆą░čéąĖčéčī ą▓ 8-ą▒ąĖčéąĮąŠąĄ, ąĮčāąČąĮąŠ ą┐čĆąŠčüč鹊 ąĄą│ąŠ ą┐ąŠą┤ąĄą╗ąĖčéčī ąĮą░ 256. ąÉ čüą║ą░č湥čé ą╗ąĖą▒ąŠ ą┐ąŠč鹊ą╝čā čćč鹊 ą┐ąŠą╝ąĄčģąĖ ą╗ąŠą▓ąĖč鹥, ą╗ąĖą▒ąŠ ąĮąĄą┐čĆą░ą▓ąĖą╗čīąĮąŠ ą┤ą░čéčćąĖą║ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ ąŠą┐čĆą░čłąĖą▓ą░ąĄč鹥.
ą×čłąĖą▒ą║ąĖ ą▓ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ (čäą░ą╣ą╗ pid.c) - ąĮąĄčé (čÅ ąŠą▒ čŹč鹊ą╝ ą┐ąĖčüą░ą╗). ą×čłąĖą▒ą║ą░ ą┤ąŠą┐čāčēąĄąĮą░ ą▓ ąŠą┐ąĖčüą░ąĮąĖąĖ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ - č鹥ą║čüčé ąĮą░ ą┤ą░ąĮąĮąŠą╝ čüą░ą╣č鹥 ąĖ ąĖčüčģąŠą┤ąĮčŗą╣ pdf ąĮą░ ą░ąĮą│ą╗ąĖą╣čüą║ąŠą╝.
ąÆčŗ čüąŠą▓ąĄčĆčłąĄąĮąĮąŠ ą┐čĆą░ą▓čŗ, čćč鹊
de(t)/dt = d(SP - y(t))/dt = -dy(t)/dt.
ąØąŠ dy(t)/dt = y(n)-y(n-1), čé.ąĄ. ąŠčé ąĘąĮą░č湥ąĮąĖčÅ ąĮą░ č鹥ą║čāčēąĄą╝ čłą░ą│ąĄ ąĮą░ą┤ąŠ ąŠčéąĮčÅčéčī ąĘąĮą░č湥ąĮąĖąĄ čü ą┐čĆąĄą┤čŗą┤čāčēąĄą│ąŠ čłą░ą│ą░.
ąÉ -dy(t)/dt = y(n-1)-y(n), čüą╗ąĄą┤ąŠą▓ą░č鹥ą╗čīąĮąŠ:
de(t)/dt = y(n-1)-y(n). ąśą╝ąĄąĮąĮąŠ čŹčéą░ č乊čĆą╝čāą╗ą░ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮą░ ą▓ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ (pid.c) - čÅ ąŠą▒ čŹč鹊ą╝ ą┐ąĖčüą░ą╗ čĆą░ąĮčīčłąĄ. ąØąŠ ą▓ąŠčé ą▓ č鹥ą║čüč鹥 ąŠą┐ąĖčüą░ąĮąĖčÅ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ą▓ ą┐ąŠčüą╗ąĄą┤ąĮąĄą╣ č乊čĆą╝čāą╗ąĄ ą▓ čĆą░ąĘą┤ąĄą╗ąĄ 2.5.1 č乊čĆą╝čāą╗ą░ ąŠčéą╗ąĖčćą░ąĄčéčüčÅ ąŠčé ą┐čĆąĖą▓ąĄą┤ąĄąĮąĮąŠą╣.
ąĢčüą╗ąĖ, ą▓čüąĄ-čéą░ą║ąĖ, ąĮąĄą┐ąŠąĮčÅčéąĮąŠ, ą┐ąŠčüą╝ąŠčéčĆąĖč鹥 ą▓ąĮąĖą╝ą░č鹥ą╗čīąĮąŠ ą╝ąŠąĖ ą║ąŠą╝ą╝ąĄąĮčéą░čĆąĖąĖ #3 ąĖ #4.
ą×čłąĖą▒ą║ąĖ ąĮąĄčé. ąóąŠčé, ą║č鹊 ą┐ąĖčüą░ą╗ čĆąĄą░ą╗ąĖąĘą░čåąĖčÄ, čģąŠčĆąŠčłąŠ čĆą░ąĘą▒ąĖčĆą░ąĄčéčüčÅ ą▓ č鹥ąŠčĆąĖąĖ ą░ą▓č鹊ą╝ą░čéąĖč湥čüą║ąŠą│ąŠ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ. e(t)=SP-y(t),
SP, ą║ą░ą║ ą┐čĆą░ą▓ąĖą╗ąŠ, = const. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝,
de(t)/dt = d(SP - y(t))/dt = -dy(t)/dt.
ąŁč鹊čé ąĖąĘčÅčēąĮčŗą╣ ą┐čĆąĖčæą╝ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┤ą╗čÅ čāčüčéčĆą░ąĮąĄąĮąĖčÅ "ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠ ą│ąŠ ą▓čüą┐ą╗ąĄčüą║ą░" ą┐čĆąĖ ąĖąĘą╝ąĄąĮąĄąĮąĖąĖ ąĘą░ą┤ą░ąĮąĖčÅ SP (setpoint).
// Calculate Dterm
d_term = pid_st->D_Factor * (pid_st->lastProcessValu e - processValue);
processValue - čŹč鹊 č鹥ą║čāčēąĄąĄ ąĘąĮą░č湥ąĮąĖąĄ ą▓čŗčģąŠą┤ąĮąŠą╣ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣, čé.ąĄ. y(n);
pid_st->lastProcessValu e - čŹč鹊 ąĘąĮą░č湥ąĮąĖąĄ ą▓čŗčģąŠą┤ąĮąŠą╣ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣ ąĮą░ ą┐čĆąĄą┤čŗą┤čāčēąĄą╝ čłą░ą│ąĄ, čé.ąĄ. y(n-1).
ą×čéčüčÄą┤ą░ čüą╗ąĄą┤čāąĄčé, čćč鹊 ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠ ąĄ čüą╗ą░ą│ą░ąĄą╝ąŠąĄ ą▓ ą║ąŠą┤ąĄ ą▓čŗčćąĖčüą╗čÅąĄčéčüčÅ ą┐ąŠ č乊čĆą╝čāą╗ąĄ
Kd*(y(n-1) - y(n)), čüą╗ąĄą┤ąŠą▓ą░č鹥ą╗čīąĮąŠ ą▓ ą┐ąŠčüą╗ąĄą┤ąĮąĄą╣ č乊čĆą╝čāą╗ąĄ ą▓ čĆą░ąĘą┤ąĄą╗ąĄ 2.5.1 ą┤ąŠą┐čāčēąĄąĮą░ ąŠčłąĖą▒ą║ą░ ą▓ ąŠčĆąĖą│ąĖąĮą░ą╗čīąĮąŠą╣ ą┤ąŠą║čāą╝ąĄąĮčéą░čåąĖąĖ.
ą”ąĖčéąĖčĆčāčÄ Alex:
ą×čłąĖą▒ą║ą░ - čŹč鹊 čĆą░ąĘąĮąŠčüčéčī ą╝ąĄąČą┤čā y0(t) ąĖ y(t), čé.ąĄ. e(t)=y0(t)-y(t) (čüą╝. čüčģąĄą╝čā ąĮą░ čĆąĖčü. 2-1).
ąÆ ą░ą╗ą│ąŠčĆąĖčéą╝ąĄ ą┤ą╗čÅ č鹊ą│ąŠ, čćč鹊ą▒čŗ ąĖąĘą▒ąĄąČą░čéčī ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ čāą┐čĆą░ą▓ą╗čÅčÄčēąĄą│ąŠ ą▓ąŠąĘą┤ąĄą╣čüčéą▓ąĖčÅ u(t) ą┐čĆąĖ ą▒čŗčüčéčĆąŠą╝ ąĖąĘą╝ąĄąĮąĄąĮąĖąĖ ąĘą░ą┤ą░čÄčēąĄą│ąŠ ą▓ąŠąĘą┤ąĄą╣čüčéą▓ąĖčÅ y0(t), ą┐čĆąĄą┤ą╗ą░ą│ą░ąĄčéčüčÅ ą┐čĆąŠą▓ąŠą┤ąĖčéčī ą┤ąĖčäč乥čĆąĄąĮčåąĖčĆąŠą▓ą░ąĮ ąĖąĄ ąĮąĄ čüąĖą│ąĮą░ą╗ą░ ąŠčłąĖą▒ą║ąĖ e(t), ą░ ą▓čŗčģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ y(t) (čé.ąĄ. ą┐ąŠą╗ą░ą│ą░ąĄčéčüčÅ, čćč鹊 y0(t)=const). ą¤ąŠčŹč鹊ą╝čā:
de(t)/dt = d/dt(y0(t) - y(t)) ~= -dy(t)/dt = -(y(n) - y(n-1)) = y(n-1) - y(n).
ąĢčüą╗ąĖ y(n) čŹč鹊 ąŠčłąĖą▒ą║ą░, č鹊 ąĮą░ą┐ąĖčüą░ąĮąŠ ą▓ąĄčĆąĮąŠ ą▓čüčæ, ąÆčŗ ąĮąĄ ą┐čĆą░ą▓čŗ. ąÉ ąĄčüą╗ąĖ y(n) čŹč鹊 ąĮąĄ ąŠčłąĖą▒ą║ą░, č鹊 ą▓ąŠąŠą▒čēąĄ ąĮąĄą┐ąŠąĮčÅčéąĮąŠ čćč鹊 čéą░ą╝ ą▓čŗčĆą░ąČą░ąĄčéčüčÅ ą▓ č乊čĆą╝čāą╗ąĄ.
RSS ą╗ąĄąĮčéą░ ą║ąŠą╝ą╝ąĄąĮčéą░čĆąĖąĄą▓ čŹč鹊ą╣ ąĘą░ą┐ąĖčüąĖ