|
ąŁč鹊 ą┐ąĄčĆąĄą▓ąŠą┤ ą░ą┐ąĮąŠčāčéą░ Atmel "AVR201: Using the AVR┬« Hardware Multiplier" [1], ą┐ąŠčüą▓čÅčēąĄąĮąĮąŠą│ąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÄ ą║ąŠą╝ą░ąĮą┤ čāą╝ąĮąŠąČąĄąĮąĖčÅ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓ AVR.
ą×ą▒čēąĖąĄ ą▓ąŠąĘą╝ąŠąČąĮąŠčüčéąĖ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ AVR, ąŠą┐ąĖčüą░ąĮąĮčŗąĄ ą▓ čŹč鹊ą╝ ą░ą┐ąĮąŠčāč鹥, ą▓ą║ą╗čÄčćą░čÄčé ą▓ čüąĄą▒čÅ:
ŌĆó 8- ąĖ 16-bit čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ.
ŌĆó ą¤ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ ą┤ą╗čÅ ąĘąĮą░ą║ąŠą▓čŗčģ (Signed) ąĖ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓čŗčģ (Unsigned) čćąĖčüąĄą╗.
ŌĆó ąöčĆąŠą▒ąĮąŠąĄ (Fractional) ąĘąĮą░ą║ąŠą▓čŗčģ (Signed) ąĖ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓čŗčģ (Unsigned) čćąĖčüąĄą╗.
ŌĆó ą¤čĆąĖą╝ąĄčĆ ą▓čŗą┐ąŠą╗ąĮčÅąĄą╝čŗčģ ą┐čĆąŠą│čĆą░ą╝ą╝.
[ąÆą▓ąĄą┤ąĄąĮąĖąĄ]
ąóąĄčĆą╝ąĖąĮ megaAVR ąŠčéąĮąŠčüąĖčéčüčÅ ą║ čüąĄčĆąĖčÅą╝ ąŠčéąĮąŠčüąĖč鹥ą╗čīąĮąŠ ąĮąŠą▓čŗčģ čāčüčéčĆąŠą╣čüčéą▓ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓ čüąĄą╝ąĄą╣čüčéą▓ą░ AVR RISC, ą║ąŠč鹊čĆąŠąĄ ą▓ą║ą╗čÄčćą░ąĄčé ą▓ čüąĄą▒čÅ, ą┐ąŠą╝ąĖą╝ąŠ ą┤čĆčāą│ąĖčģ ąĮąŠą▓čŗčģ čāą╗čāčćčłąĄąĮąĖą╣, čéą░ą║ąČąĄ ąĖ ą░ą┐ą┐ą░čĆą░čéąĮčŗą╣ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī. ąŁč鹊čé ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī ą╝ąŠąČąĄčé ą┐ąĄčĆąĄą╝ąĮąŠąČą░čéčī ą┤ą▓ą░ 8-ą▒ąĖčéąĮčŗčģ čćąĖčüą╗ą░, ą▓čŗą┤ą░ą▓ą░čÅ 16-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé č鹊ą╗čīą║ąŠ ąĘą░ 2 čéą░ą║č鹊ą▓čŗčģ čåąĖą║ą╗ą░. ą¤ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī ą╝ąŠąČąĄčé ąŠą▒čĆą░ą▒ąŠčéą░čéčī čćąĖčüą╗ą░ čüąŠ ąĘąĮą░ą║ąŠą╝, ąĖ čćąĖčüą╗ą░ ą▒ąĄąĘ ąĘąĮą░ą║ą░, ąĖ ą┤čĆąŠą▒ąĮčŗąĄ čćąĖčüą╗ą░ ą▒ąĄąĘ čāą╝ąĄąĮčīčłąĄąĮąĖčÅ čüą║ąŠčĆąŠčüčéąĖ ąĖ ą▒ąĄąĘ ą╗ąĖčłąĮąĖčģ ąĘą░čéčĆą░čé ą║ąŠą┤ą░. ą¤ąĄčĆą▓ą░čÅ čüąĄą║čåąĖčÅ čŹč鹊ą│ąŠ ą┤ąŠą║čāą╝ąĄąĮčéą░ ą┤ą░čüčé ąĮąĄą║ąŠč鹊čĆčŗąĄ ą┐čĆąĖą╝ąĄčĆčŗ ą┐ąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÄ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ ą▓ 8-ą▒ąĖčéąĮąŠą╣ ą░čĆąĖčäą╝ąĄčéąĖą║ąĄ.
ą¦č鹊ą▒čŗ ą╝ąŠąČąĮąŠ ą▒čŗą╗ąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čī, ą▓ čüąĖčüč鹥ą╝čā ą║ąŠą╝ą░ąĮą┤ AVR ą▒čŗą╗ąĖ ą┤ąŠą▒ą░ą▓ą╗ąĄąĮčŗ 6 ąĮąŠą▓čŗčģ ąĖąĮčüčéčĆčāą║čåąĖą╣:
ŌĆó MUL, čāą╝ąĮąŠąČąĄąĮąĖąĄ čåąĄą╗čŗčģ čćąĖčüąĄą╗ ą▒ąĄąĘ ąĘąĮą░ą║ą░ (unsigned integer).
ŌĆó MULS, čāą╝ąĮąŠąČąĄąĮąĖąĄ čåąĄą╗čŗčģ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed integer).
ŌĆó MULSU, čāą╝ąĮąŠąČąĄąĮąĖąĄ signed integer ąĮą░ unsigned integer.
ŌĆó FMUL, čāą╝ąĮąŠąČąĄąĮąĖąĄ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ ą▒ąĄąĘ ąĘąĮą░ą║ą░ (unsigned fractional).
ŌĆó FMULS, čāą╝ąĮąŠąČąĄąĮąĖąĄ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed fractional).
ŌĆó FMULSU, čāą╝ąĮąŠąČąĄąĮąĖąĄ signed fractional ąĮą░ unsigned fractional.
ą×čéą┤ąĄą╗čīąĮčŗąĄ ąĖąĮčüčéčĆčāą║čåąĖąĖ MULSU ąĖ FMULSU ą┤ąŠą▒ą░ą▓ą╗ąĄąĮčŗ ą┤ą╗čÅ čāą╗čāčćčłąĄąĮąĖčÅ čüą║ąŠčĆąŠčüčéąĖ ąĖ ą┐ą╗ąŠčéąĮąŠčüčéąĖ ą║ąŠą┤ą░ ą┐čĆąĖ čāą╝ąĮąŠąČąĄąĮąĖąĖ 16-ą▒ąĖčéąĮčŗčģ ąŠą┐ąĄčĆą░ąĮą┤ąŠą▓. ąÆąŠ ą▓č鹊čĆąŠą╣ čüąĄą║čåąĖąĖ ą▒čāą┤čāčé ą┐ąŠą║ą░ąĘą░ąĮčŗ ą┐čĆąĖą╝ąĄčĆčŗ, ą║ą░ą║ čŹčäč乥ą║čéąĖą▓ąĮąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī čāą╝ąĮąŠąČąĖč鹥ą╗čī ą┤ą╗čÅ 16-bit ą░čĆąĖčäą╝ąĄčéąĖą║ąĖ.
ąÜąŠą╝ą┐ąŠąĮąĄąĮč鹊ą╝, ą║ąŠč鹊čĆčŗą╣ ą┤ąĄą╗ą░ąĄčé ą▓čŗą┤ąĄą╗ąĄąĮąĮčŗą╣ čåąĖčäčĆąŠą▓ąŠą╣ čüąĖą│ąĮą░ą╗čīąĮčŗą╣ ą┐čĆąŠčåąĄčüčüąŠčĆ čüą┐ąĄčåąĖą░ą╗čīąĮąŠ ą┐čĆąĄą┤ąĮą░ąĘąĮą░č湥ąĮąĮčŗą╝ ą┤ą╗čÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ čüąĖą│ąĮą░ą╗ąŠą▓, čÅą▓ą╗čÅąĄčéčüčÅ čéą░ą║ ąĮą░ąĘčŗą▓ą░ąĄą╝čŗą╣ čāąĘąĄą╗ čāą╝ąĮąŠąČąĄąĮąĖčÅ čü ą┤ąŠą▒ą░ą▓ą╗ąĄąĮąĖąĄą╝ (Multiply-Accumulate unit, MAC). ąŁč鹊čé čāąĘąĄą╗ čäčāąĮą║čåąĖąŠąĮą░ą╗čīąĮąŠ 菹║ą▓ąĖą▓ą░ą╗ąĄąĮč鹥ąĮ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÄ, ąĮą░ą┐čĆčÅą╝čāčÄ čüąŠąĄą┤ąĖąĮąĄąĮąĮąŠą╝čā čü čāąĘą╗ąŠą╝ ą░čĆąĖčäą╝ąĄčéąĖą║ąĖ ąĖ ą╗ąŠą│ąĖą║ąĖ (Arithmetic Logic Unit, ALU). ą£ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆčŗ megaAVR čĆą░ąĘčĆą░ą▒ąŠčéą░ąĮčŗ čéą░ą║, čćč鹊ą▒čŗ ą┐čĆąĄą┤ąŠčüčéą░ą▓ąĖčéčī čüąĄą╝ąĄą╣čüčéą▓čā AVR ą▓ąŠąĘą╝ąŠąČąĮąŠčüčéčī čŹčäč乥ą║čéąĖą▓ąĮąŠ ą▓čŗą┐ąŠą╗ąĮčÅčéčī čéą░ą║čāčÄ ąČąĄ multiply-accumulate ąŠą┐ąĄčĆą░čåąĖčÄ. ąÆ čŹč鹊ą╝ ą░ą┐ąĮąŠčāč鹥 ą▒čāą┤čāčé čĆą░čüčüą╝ąŠčéčĆąĄąĮčŗ ą┐čĆąĖą╝ąĄčĆčŗ čĆąĄą░ą╗ąĖąĘą░čåąĖąĖ ąŠą┐ąĄčĆą░čåąĖąĖ MAC.
ą×ą┐ąĄčĆą░čåąĖčÅ Multiply-Accumulate (ą║ąŠč鹊čĆą░čÅ ąĖąĮąŠą│ą┤ą░ ąĮą░ąĘčŗą▓ą░ąĄčéčüčÅ ą║ą░ą║ multiply-add) ąĖą╝ąĄąĄčé ąŠą┤ąĖąĮ ą║čĆąĖčéąĖč湥čüą║ąĖą╣ ąĮąĄą┤ąŠčüčéą░č鹊ą║. ąÜąŠą│ą┤ą░ ą┤ąŠą▒ą░ą▓ą╗čÅčÄčéčüčÅ ąĮąĄčüą║ąŠą╗čīą║ąŠ ąĘąĮą░č湥ąĮąĖą╣ ą║ ąŠą┤ąĮąŠą╝čā ąĘąĮą░č湥ąĮąĖčÄ čĆąĄąĘčāą╗čīčéą░čéą░, ą┤ą░ąČąĄ ą║ąŠą│ą┤ą░ ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮčŗąĄ ąĖ ąŠčéčĆąĖčåą░č鹥ą╗čīąĮčŗąĄ ąĘąĮą░č湥ąĮąĖčÅ ą╝ąŠą│čāčé ą║ąŠą╝ą┐ąĄąĮčüąĖčĆąŠą▓ą░čéčī ą┤čĆčāą│ ą┤čĆčāą│ą░, ąĖą╝ąĄąĄčéčüčÅ čĆąĖčüą║ ą┐ąĄčĆąĄą┐ąŠą╗ąĮąĄąĮąĖčÅ čĆąĄąĘčāą╗čīčéą░čéą░, čćč鹊 čüčéą░ąĮąŠą▓ąĖčéčüčÅ ąŠč湥ą▓ąĖą┤ąĮčŗą╝. ąóąŠ ąĄčüčéčī, ą┤ąŠą▒ą░ą▓ą╗čÅčÅ ą║ ą┐čĆąĖą╝ąĄčĆčā ąĄą┤ąĖąĮąĖčåčā ą║ signed ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣-ą▒ą░ą╣čéčā, ą║ąŠč鹊čĆą░čÅ čüąŠą┤ąĄčƹȹĖčé +127, čĆąĄąĘčāą╗čīčéą░čé ą▓ą┤čĆčāą│ čüčéą░ąĮąĄčé -128, ą▓ą╝ąĄčüč鹊 č鹊ą│ąŠ čćč鹊ą▒čŗ čüčéą░čéčī +128. ą×ą┤ąĖąĮ ąĖąĘ čüą┐ąŠčüąŠą▒ąŠą▓, ą║ąŠč鹊čĆčŗą╣ čćą░čüč鹊 ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┤ą╗čÅ čĆąĄčłąĄąĮąĖčÅ čŹč鹊ą╣ ą┐čĆąŠą▒ą╗ąĄą╝čŗ, ą▓ąŠą▓ą╗ąĄą║ą░ąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗, ąĮą░ą┐čĆąĖą╝ąĄčĆ čćąĖčüąĄą╗, ą║ąŠč鹊čĆčŗąĄ ą╝ąĄąĮčīčłąĄ 1 ąĖ ą▒ąŠą╗čīčłąĄ ąĖą╗ąĖ čĆą░ą▓ąĮčŗ -1. ąÆ ą┐ąŠčüą╗ąĄą┤ąĮąĄą╣ čüąĄą║čåąĖąĖ ą▒čāą┤čāčé čĆą░čüčüą╝ąŠčéčĆąĄąĮčŗ ąĮąĄą║ąŠč鹊čĆčŗąĄ ą┐čĆąŠą▒ą╗ąĄą╝čŗ, ą║ą░čüą░čÄčēąĖąĄčüčÅ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗.
ąÆ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖąĄ ą║ ąĮąŠą▓ąŠą╣ ąĖąĮčüčéčĆčāą║čåąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ, ą║ čÅą┤čĆčā megaAVR ą┤ąŠą▒ą░ą▓ą╗ąĄąĮčŗ ąĖ ąĮąĄčüą║ąŠą╗čīą║ąŠ ą┤čĆčāą│ąĖčģ ąĖąĘą╝ąĄąĮąĄąĮąĖą╣ ąĖ čāą╗čāčćčłąĄąĮąĖą╣. ą×ą┤ąĮąŠ ąĖąĘ ąĮąĖčģ - čāą┤ąŠą▒ąĮą░čÅ ą▓ ąĮąĄą║ąŠč鹊čĆčŗčģ čüą╗čāčćą░čÅčģ ąĮąŠą▓ą░čÅ ąĖąĮčüčéčĆčāą║čåąĖčÅ MOVW (ą║ąŠą┐ąĖčĆąŠą▓ą░ąĮąĖąĄ čĆąĄą│ąĖčüčéčĆąŠą▓ąŠą│ąŠ čüą╗ąŠą▓ą░, Copy Register Word), ą║ąŠč鹊čĆą░čÅ ą▓čŗą┐ąŠą╗ąĮčÅąĄčé ą║ąŠą┐ąĖčĆąŠą▓ą░ąĮąĖąĄ ąŠą┤ąĮąŠą╣ čĆąĄą│ąĖčüčéčĆąŠą▓ąŠą╣ ą┐ą░čĆčŗ ą▓ ą┤čĆčāą│čāčÄ čĆąĄą│ąĖčüčéčĆąŠą▓čāčÄ ą┐ą░čĆčā.
ążą░ą╣ą╗ AVR201.asm čüąŠą┤ąĄčƹȹĖčé ąĖčüčģąŠą┤ąĮčŗą╣ ą║ąŠą┤ ą┤ą╗čÅ čŹč鹊ą│ąŠ ą░ą┐ąĮąŠčāčéą░, ą│ą┤ąĄ ą┐čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ 16-ą▒ąĖčéąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ. ąĪą┐ąĖčüąŠą║ ą▓čüąĄčģ čĆąĄą░ą╗ąĖąĘą░čåąĖą╣ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ čü čāą║ą░ąĘą░ąĮąĖąĄą╝ ąĖčģ ą▒čŗčüčéčĆąŠą┤ąĄą╣čüčéą▓ąĖčÅ ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą▓ čüą╗ąĄą┤čāčÄčēąĖčģ čéą░ą▒ą╗ąĖčåą░čģ.
| ą¤ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ 8-bit * 8-bit |
Cą╗ąŠą▓ ą║ąŠą┤ą░ (čåąĖą║ą╗ąŠą▓ CPU) |
| ąæąĄąĘąĘąĮą░ą║ąŠą▓ąŠąĄ (unsigned) čāą╝ąĮąŠąČąĄąĮąĖąĄ 8 * 8 = 16 bit |
1 (2) |
| ąŚąĮą░ą║ąŠą▓ąŠąĄ (signed) čāą╝ąĮąŠąČąĄąĮąĖąĄ 8 * 8 = 16 bit |
1 (2) |
| ąöčĆąŠą▒ąĮąŠąĄ signed/unsigned čāą╝ąĮąŠąČąĄąĮąĖąĄ 8 * 8 = 16 bit |
1 (2) |
| ąöčĆąŠą▒ąĮą░čÅ signed ąŠą┐ąĄčĆą░čåąĖčÅ MAC 8 * 8 = 16 bit |
3 (4) |
| ą¤ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ 16-bit * 16-bit |
Cą╗ąŠą▓ ą║ąŠą┤ą░ (čåąĖą║ą╗ąŠą▓ CPU) |
| ąŻą╝ąĮąŠąČąĄąĮąĖąĄ signed/unsigned 16 * 16 = 16 bit |
6 (9) |
| ąŻą╝ąĮąŠąČąĄąĮąĖąĄ unsigned 16 * 16 = 32 bit |
13 (17) |
| ąŻą╝ąĮąŠąČąĄąĮąĖąĄ signed 16 * 16 = 32 bit |
15 (19) |
| MAC signed 16 * 16 += 32 bit |
19 (23) |
| ąöčĆąŠą▒ąĮąŠąĄ signed čāą╝ąĮąŠąČąĄąĮąĖąĄ 16 * 16 = 32 bit |
16 (20) |
| ąöčĆąŠą▒ąĮąŠąĄ signed MAC 16 * 16 += 32 bit |
21 (25) |
| ąŻą╝ąĮąŠąČąĄąĮąĖąĄ unsigned 16 * 16 = 24 bit |
10 (14) |
| ąŻą╝ąĮąŠąČąĄąĮąĖąĄ signed 16 * 16 = 24 bit |
10 (14) |
| ąŻą╝ąĮąŠąČąĄąĮąĖąĄ signed MAC 16 * 16 += 24 bit |
12 (16) |
[8-čĆą░ąĘčĆčÅą┤ąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ (8-bit Multiplication)]
8-ą▒ąĖčéąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ ą┐čĆąŠčüč鹊, čćč鹊 čģąŠčĆąŠčłąŠ ą┐ąŠą║ą░ąĘčŗą▓ą░čÄčé ą┐čĆąĖą╝ąĄčĆčŗ ą▓ čŹč鹊ą╣ čüąĄą║čåąĖąĖ. ą¤čĆąŠčüč鹊 ąĘą░ą│čĆčāąĘąĖč鹥 ąŠą┐ąĄčĆą░ąĮą┤čŗ ą▓ ą┤ą▓ą░ čĆąĄą│ąĖčüčéčĆą░ (ąĖą╗ąĖ č鹊ą╗čīą║ąŠ ąŠą┤ąĖąĮ ą┤ą╗čÅ ą▓ąŠąĘą▓ąĄą┤ąĄąĮąĖčÅ ą▓ ą║ą▓ą░ą┤čĆą░čé), ąĖ ą▓čŗą┐ąŠą╗ąĮąĖč鹥 ąŠą┤ąĮčā ąĖąĘ ąĮąĄčüą║ąŠą╗čīą║ąĖčģ ąĖąĮčüčéčĆčāą║čåąĖą╣ čāą╝ąĮąŠąČąĄąĮąĖčÅ. ąĀąĄąĘčāą╗čīčéą░čé ą▒čāą┤ąĄčé ą┐ąŠą╝ąĄčēąĄąĮ ą▓ čĆąĄą│ąĖčüčéčĆąŠą▓čāčÄ ą┐ą░čĆčā R1:R0. ą×ą┤ąĮą░ą║ąŠ ąĖą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 č鹊ą╗čīą║ąŠ ąĖąĮčüčéčĆčāą║čåąĖčÅ MUL ąĮąĄ ąĖą╝ąĄąĄčé ąŠą│čĆą░ąĮąĖč湥ąĮąĖą╣ ąĮą░ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čĆąĄą│ąĖčüčéčĆąŠą▓. ąØą░ čĆąĖčüčāąĮą║ąĄ 1 ą┐ąŠą║ą░ąĘą░ąĮčŗ ą┤ąŠą┐čāčüčéąĖą╝čŗąĄ ą▓ą░čĆąĖą░ąĮčéčŗ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ čĆąĄą│ąĖčüčéčĆąŠą▓ ą▓ ą║ą░č湥čüčéą▓ąĄ ąŠą┐ąĄčĆą░ąĮą┤ąŠą▓ ą┤ą╗čÅ ą║ą░ąČą┤ąŠą╣ ąĖčģ ąĖąĮčüčéčĆčāą║čåąĖą╣ čāą╝ąĮąŠąČąĄąĮąĖčÅ.
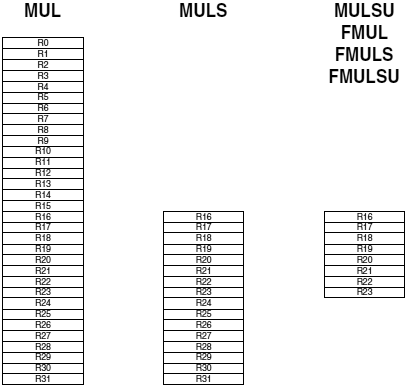
ąĀąĖčü. 1. ąöąŠą┐čāčüčéąĖą╝ąŠąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čĆąĄą│ąĖčüčéčĆąŠą▓ ą┤ą╗čÅ ąĖąĮčüčéčĆčāą║čåąĖą╣ čāą╝ąĮąŠąČąĄąĮąĖčÅ.
ą¤čĆąĖą╝ąĄčĆ 1 - ą▒ą░ąĘąŠą▓ąŠąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ąĖąĮčüčéčĆčāą║čåąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ
ąÆ čŹč鹊ą╝ ą┐čĆąĖą╝ąĄčĆąĄ ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą║ąŠą┤ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░, ą║ąŠč鹊čĆčŗą╣ čćąĖčéą░ąĄčé ą▓čģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĖąĘ ą┐ąŠčĆčéą░ B, čāą╝ąĮąŠąČą░ąĄčé ąĄą│ąŠ ąĮą░ ą║ąŠąĮčüčéą░ąĮčéčā 5, ąĖ ąĘą░č鹥ą╝ čüąŠčģčĆą░ąĮčÅąĄčé čĆąĄąĘčāą╗čīčéą░čé ą▓ čĆąĄą│ąĖčüčéčĆąŠą▓ąŠą╣ ą┐ą░čĆąĄ R17:R16.
1
2
3
4
5
|
in r16,PINB ; ą¤čĆąŠčćąĖčéą░čéčī ąĘąĮą░č湥ąĮąĖąĄ ąĖąĘ ą╗ąŠą│ąĖč湥čüą║ąĖčģ čāčĆąŠą▓ąĮąĄą╣
; ą▓čŗą▓ąŠą┤ąŠą▓ ąĮąŠąČąĄą║ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ą┐ąŠčĆčéą░ B.
ldi r17,5 ; ąŚą░ą│čĆčāąĘąĖčéčī ą║ąŠąĮčüčéą░ąĮčéčā 5 ą▓ čĆąĄą│ąĖčüčéčĆ r17.
mul r16,r17 ; r1:r0 = r17 * r16
movw r17:r16,r1:r0 ; ą¤ąĄčĆąĄą╝ąĄčüčéąĖčéčī čĆąĄąĘčāą╗čīčéą░čé ą▓ čĆąĄą│ąĖčüčéčĆąŠą▓čāčÄ ą┐ą░čĆčā r17:r16.
|
ą×ą▒čĆą░čéąĖč鹥 ą▓ąĮąĖą╝ą░ąĮąĖąĄ, čćč鹊 ąĘą┤ąĄčüčī ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ąĮąŠą▓ą░čÅ ąĖąĮčüčéčĆčāą║čåąĖčÅ MOVW. ąŁč鹊čé ą┐čĆąĖą╝ąĄčĆ ą┤ąŠą┐čāčüčéąĖą╝ ą┤ą╗čÅ ą▓čüąĄčģ ąĖąĮčüčéčĆčāą║čåąĖą╣ čāą╝ąĮąŠąČąĄąĮąĖčÅ.
ą¤čĆąĖą╝ąĄčĆ 2 ŌĆō čüą┐ąĄčåąĖą░ą╗čīąĮčŗąĄ čüą╗čāčćą░ąĖ
ąŁč鹊čé ą┐čĆąĖą╝ąĄčĆ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ąĮąĄą║ąŠč鹊čĆčŗąĄ ąŠčüąŠą▒čŗąĄ čüą╗čāčćą░ąĖ ą┤ąŠą┐čāčüčéąĖą╝ąŠą│ąŠ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖčÅ ąĖąĮčüčéčĆčāą║čåąĖąĖ MUL.
1
2
3
4
5
6
|
;ą¤ąĄčĆąĄą╝ąĄąĮąĮčŗąĄ A ąĖ B ąĮą░čģąŠą┤čÅčéčüčÅ ą▓ čÅč湥ą╣ą║ą░čģ ą┐ą░ą╝čÅčéąĖ SRAM.
lds r0,variableA ; ąŚą░ą│čĆčāąĘą║ą░ ą▓ r0 ąĘąĮą░č湥ąĮąĖčÅ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣ A.
lds r1,variableB ; ąŚą░ą│čĆčāąĘą║ą░ ą▓ r1 ąĘąĮą░č湥ąĮąĖčÅ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣ B.
mul r1,r0 ; r1:r0 = variable A * variable B
lds r0,variableA ; ąŚą░ą│čĆčāąĘą║ą░ ą▓ r0 ąĘąĮą░č湥ąĮąĖčÅ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣ A.
mul r0,r0 ; r1:r0 = square(variable A) - ą║ą▓ą░ą┤čĆą░čé A.
|
ąöą░ąČąĄ ąĄčüą╗ąĖ ąŠą┐ąĄčĆą░ąĮą┤ ą┐ąŠą╝ąĄčēąĄąĮ ą▓ čĆąĄą│ąĖčüčéčĆąŠą▓čāčÄ ą┐ą░čĆčā R1:R0 (ą║ąŠč鹊čĆą░čÅ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┤ą╗čÅ čĆąĄąĘčāą╗čīčéą░čéą░ čāą╝ąĮąŠąČąĄąĮąĖčÅ), ąŠą┐ąĄčĆą░čåąĖčÅ čāą╝ąĮąŠąČąĄąĮąĖčÅ ą▓čüąĄ čĆą░ą▓ąĮąŠ ą┤ą░čüčé ą║ąŠčĆčĆąĄą║čéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé, ą┐ąŠčüą║ąŠą╗čīą║čā ąĘąĮą░č湥ąĮąĖčÅ R1 ąĖ R0 ą▒čāą┤čāčé ąĘą░čģą▓ą░č湥ąĮčŗ ą┐ąŠ ą┐ąĄčĆą▓ąŠą╝čā čåąĖą║ą╗čā čéą░ą║č鹊ą▓, ąĖ čĆąĄąĘčāą╗čīčéą░čé ąŠą┐ąĄčĆą░čåąĖąĖ ą▒čāą┤ąĄčé čüąŠčģčĆą░ąĮąĄąĮ ąŠą▒čĆą░čéąĮąŠ ąĮą░ ą▓č鹊čĆąŠą╝ čåąĖą║ą╗ąĄ čéą░ą║č鹊ą▓.
ą¤čĆąĖą╝ąĄčĆ 3 - ąŠą┐ąĄčĆą░čåąĖčÅ MAC
ą¤ąŠčüą╗ąĄą┤ąĮąĖą╣ ą┐čĆąĖą╝ąĄčĆ ą▓ čŹč鹊ą╣ čüąĄą║čåąĖąĖ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čĆąĄą░ą╗ąĖąĘą░čåąĖčÄ ąŠą┐ąĄčĆą░čåąĖąĖ multiply-accumulate (čāą╝ąĮąŠąČąĄąĮąĖąĄ čü ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄą╝). ą×čüąĮąŠą▓ąĮą░čÅ č乊čĆą╝čāą╗ą░ ą┤ą╗čÅ čŹč鹊ą╣ ąŠą┐ąĄčĆą░čåąĖąĖ ą╝ąŠąČąĄčé ą▒čŗčéčī ąĮą░ą┐ąĖčüą░ąĮą░ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝:
c(n) = a(n) * b + c(n ŌĆō 1)
ąÆąŠčé ą║ąŠą┤, ą║ąŠč鹊čĆčŗą╣ ą▓čŗą┐ąŠą╗ąĮčÅąĄčé ąŠą┐ąĄčĆą░čåąĖčÄ MAC:
1
2
3
4
5
6
|
in r18,PINB ; ą¤čĆąŠčćąĖčéą░čéčī ąĘąĮą░č湥ąĮąĖąĄ ąĖąĘ ą╗ąŠą│ąĖč湥čüą║ąĖčģ čāčĆąŠą▓ąĮąĄą╣
; ą▓čŗą▓ąŠą┤ąŠą▓ ąĮąŠąČąĄą║ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ ą┐ąŠčĆčéą░ B.
ldi r19,b ; ąŚą░ą│čĆčāąĘąĖčéčī ą║ąŠąĮčüčéą░ąĮčéčā b ą▓ čĆąĄą│ąĖčüčéčĆ r19.
muls r19,r18 ; r1:r0 = variable A * variable B
add r16,r0 ; r17:r16 += r1:r0
adc r17,r1 ; r17:r16 = r18 * r19 + r17:r16
|
ą×ą▒čŗčćąĮąŠąĄ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄ ąŠą┐ąĄčĆą░čåąĖąĖ multiply-accumulate - ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą┤ą╗čÅ čäąĖą╗čīčéčĆąŠą▓ FIR (Finite Impulse Response) ąĖ IIR (Infinite Impulse Response), čĆąĄą│čāą╗čÅč鹊čĆčŗ PID ąĖ FFT (Fast Fourier Transform) [3]. ąöą╗čÅ čŹčéąĖčģ ą┐čĆąĖą╗ąŠąČąĄąĮąĖą╣ ą╝ąŠąČąĄčé ą▒čŗčéčī čāą┤ąŠą▒ąĮąŠą╣ ąĖąĮčüčéčĆčāą║čåąĖčÅ FMULS. ąōą╗ą░ą▓ąĮčŗą╣ ą▓čŗąĖą│čĆčŗčł ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ąĖąĮčüčéčĆčāą║čåąĖąĖ FMULS ą▓ą╝ąĄčüč鹊 MULS ą▓ č鹊ą╝, čćč鹊 16-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé ąŠą┐ąĄčĆą░čåąĖąĖ FMULS ą▓čüąĄą│ą┤ą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ą░ą┐ą┐čĆąŠą║čüąĖą╝ąĖčĆąŠą▓ą░ąĮ ą║ (č湥čéą║ąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĮąŠą╝čā) 8-ą▒ąĖčéąĮąŠą╝čā č乊čĆą╝ą░čéčā. ąŁč鹊 ą▒čāą┤ąĄčé ąŠą▒čüčāąČą┤ą░čéčīčüčÅ ą┤ą░ą╗ąĄąĄ ą▓ čüąĄą║čåąĖąĖ "ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ (Fractional Numbers)".
[16-čĆą░ąĘčĆčÅą┤ąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ (16-bit Multiplication)]
ąØąŠą▓čŗąĄ ąĖąĮčüčéčĆčāą║čåąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ čüą┐ąĄčåąĖą░ą╗čīąĮąŠ čĆą░ąĘčĆą░ą▒ąŠčéą░ąĮčŗ ą┤ą╗čÅ čāą╗čāčćčłąĄąĮąĖčÅ 16-bit čāą╝ąĮąŠąČąĄąĮąĖčÅ. ąÆ čŹč鹊ą╣ čüąĄą║čåąĖąĖ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮčŗ čĆąĄčłąĄąĮąĖčÅ ą┤ą╗čÅ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ą░ą┐ą┐ą░čĆą░čéąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĮąŠąČąĖč鹥ą╗čÅ čü 16-bit ąŠą┐ąĄčĆą░ąĮą┤ą░ą╝ąĖ.
ąØą░ čĆąĖčü. 2 čüčģąĄą╝ą░čéąĖč湥čüą║ąĖ ą┐čĆąŠąĖą╗ą╗čÄčüčéčĆąĖčĆąŠą▓ą░ąĮ ąŠčüąĮąŠą▓ąĮąŠą╣ ą░ą╗ą│ąŠčĆąĖčéą╝ čāą╝ąĮąŠąČąĄąĮąĖčÅ ą┤ą▓čāčģ 16-bit čćąĖčüąĄą╗ čü ą┐ąŠą╗čāč湥ąĮąĖąĄą╝ 32-bit čĆąĄąĘčāą╗čīčéą░čéą░ (C = A ŌĆó B). AH ąŠą▒ąŠąĘąĮą░čćą░ąĄčé čüčéą░čĆčłąĖą╣ ą▒ą░ą╣čé ąĖ AL ą╝ą╗ą░ą┤čłąĖą╣ ą▒ą░ą╣čé ąŠą┐ąĄčĆą░ąĮą┤ą░ A. CMH ąŠą▒ąŠąĘąĮą░čćą░ąĄčé čüčĆąĄą┤ąĮąĖą╣ čüčéą░čĆčłąĖą╣ ą▒ą░ą╣čé ąĖ CML čüčĆąĄą┤ąĮąĖą╣ ą╝ą╗ą░ą┤čłąĖą╣ ą▒ą░ą╣čé čĆąĄąĘčāą╗čīčéą░čéą░ C. ąÉąĮą░ą╗ąŠą│ąĖčćąĮčŗąĄ ąĮąŠčéą░čåąĖąĖ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ ąĖ ą┤ą╗čÅ ąŠčüčéą░ą╗čīąĮčŗčģ ą▒ą░ą╣čé.

ąĀąĖčü. 2. ą×čüąĮąŠą▓ąĮąŠą╣ ą░ą╗ą│ąŠčĆąĖčéą╝ 16-čĆą░ąĘčĆčÅą┤ąĮąŠą│ąŠ čāą╝ąĮąŠąČąĄąĮąĖčÅ.
ąÉą╗ą│ąŠčĆąĖčéą╝ čÅą▓ą╗čÅąĄčéčüčÅ ą▒ą░ąĘąŠą▓čŗą╝ ą┤ą╗čÅ ą▓čüąĄčģ čāą╝ąĮąŠąČąĄąĮąĖą╣. ąÆčüąĄ ąŠčéą┤ąĄą╗čīąĮčŗąĄ 16-ą▒ąĖčéąĮčŗąĄ čĆąĄąĘčāą╗čīčéą░čéčŗ čüą┤ą▓ąĖą│ą░čÄčéčüčÅ ąĖ čüą║ą╗ą░ą┤čŗą▓ą░čÄčéčüčÅ ą┤čĆčāą│ čü ą┤čĆčāą│ąŠą╝. ąŚąĮą░ą║ąŠą▓ąŠąĄ čĆą░čüčłąĖčĆąĄąĮąĖąĄ (sign ext) ąĮčāąČąĮąŠ č鹊ą╗čīą║ąŠ ą┤ą╗čÅ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed), ąŠą┤ąĮą░ą║ąŠ ąĖą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖąĄ ą▒ąĖčéą░ ą┐ąĄčĆąĄąĮąŠčüą░ (carry) ą┤ąŠą╗ąČąĮąŠ ą▒čŗčéčī čāčćč鹥ąĮąŠ ą┤ą╗čÅ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓čŗčģ čćąĖčüąĄą╗ (unsigned).
ą×ą┐ąĄčĆą░čåąĖčÅ 16-bit * 16-bit = 16-bit
ąŁčéą░ ąŠą┐ąĄčĆą░čåąĖčÅ ą┤ąŠą┐čāčüčéąĖą╝ą░ ąĖ ą┤ą╗čÅ čćąĖčüąĄą╗ unsigned, ąĖ ą┤ą╗čÅ čćąĖčüąĄą╗ signed, ą┤ą░ąČąĄ ąĄčüą╗ąĖ ąĮčāąČąĮą░ č鹊ą╗čīą║ąŠ ąĖąĮčüčéčĆčāą║čåąĖčÅ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ąŠą│ąŠ čāą╝ąĮąŠąČąĄąĮąĖčÅ (MUL). ąŁč鹊 ąĖą╗ą╗čÄčüčéčĆąĖčĆčāąĄčéčüčÅ ąĮą░ čĆąĖčü. 3. ą£ą░č鹥ą╝ą░čéąĖč湥čüą║ąŠąĄ ąŠą▒čŖčÅčüąĮąĄąĮąĖąĄ čüą╗ąĄą┤čāčÄčēąĄąĄ: ą║ąŠą│ą┤ą░ A ąĖ B čÅą▓ą╗čÅčÄčéčüčÅ ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮčŗą╝ąĖ čćąĖčüą╗ą░ą╝ąĖ, ąĖą╗ąĖ ą║ą░ą║ ą╝ąĖąĮąĖą╝čāą╝ ąŠą┤ąĮąŠ ąĖąĘ ąĮąĖčģ čĆą░ą▓ąĮąŠ 0, ą░ą╗ą│ąŠčĆąĖčéą╝ ą┐ąŠą╗ąĮąŠčüčéčīčÄ ą║ąŠčĆčĆąĄą║č鹥ąĮ, ą┐čĆąĄą┤ąŠčüčéą░ą▓ą╗čÅčÅ čĆąĄąĘčāą╗čīčéą░čé C = A ŌĆó B ą╝ąĄąĮčīčłąĄ 2^16, ąĄčüą╗ąĖ čĆąĄąĘčāą╗čīčéą░čé ą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą║ą░ą║ čćąĖčüą╗ąŠ unsigned, ąĖą╗ąĖ ą╝ąĄąĮčīčłąĄ 2^15, ąĄčüą╗ąĖ čĆąĄąĘčāą╗čīčéą░čé ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą║ą░ą║ čćąĖčüą╗ąŠ signed. ąĢčüą╗ąĖ ąŠą▒ą░ ą╝ąĮąŠąČąĖč鹥ą╗čÅ ąŠčéčĆąĖčåą░č鹥ą╗čīąĮčŗ, č鹊 ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ąĮąŠčéą░čåąĖčÅ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖčÅ ą┤ąŠ ą┤ą▓čāčģ (twoŌĆÖs complement); A = 2^16 - |A| ąĖ B = 2^16 - |B|:
C = A ŌĆó B = (2^16 - |A|) ŌĆó (216 - |B|) = |A ŌĆó B| + 2^32 - 2^16 ŌĆó (|A| + |B|)
ąÆ ą┤ą░ąĮąĮąŠą╝ čüą╗čāčćą░ąĄ čāčćąĖčéčŗą▓ą░čÄčéčüčÅ č鹊ą╗čīą║ąŠ 16 ą╝ą╗ą░ą┤čłąĖčģ ą▒ąĖčé; ą┐ąŠčüą╗ąĄą┤ąĮčÅčÅ čćą░čüčéčī čüčāą╝ą╝čŗ ąŠčéą▒čĆą░čüčŗą▓ą░ąĄčéčüčÅ, ąĖ ą╝čŗ ą┐ąŠą╗čāčćąĖą╝ ą║ąŠčĆčĆąĄą║čéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé C = C = |A ŌĆó B|.
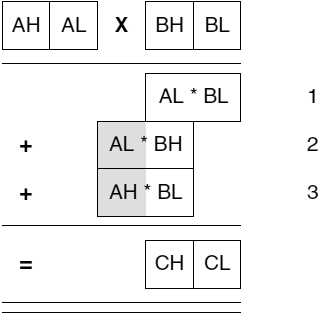
ąĀąĖčü. 3. 16-ą▒ąĖčéąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ, 16-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé.
ąÜąŠą│ą┤ą░ ąŠą┤ąĖąĮ ą╝ąĮąŠąČąĖč鹥ą╗čī ąŠčéčĆąĖčåą░č鹥ą╗čīąĮčŗą╣ ąĖ ą┤čĆčāą│ąŠą╣ ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮčŗą╣, ąĮą░ą┐čĆąĖą╝ąĄčĆ A ąŠčéčĆąĖčåą░č鹥ą╗čīąĮčŗą╣ ąĖ B ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮčŗą╣:
C = A ŌĆó B = (2^16 - |A|) ŌĆó |B| = (2^16 ŌĆó |B|) - |A ŌĆó B| = (2^16 - |A ŌĆó B|) + 2^16 ŌĆó (|B| - 1)
ąĪčéą░čĆčłąĖąĄ ą▒ąĖčéčŗ ą▒čāą┤čāčé ąŠčéą▒čĆąŠčłąĄąĮčŗ ąĖ ą║ąŠčĆčĆąĄą║čéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé čü ąĮąŠčéą░čåąĖąĄą╣ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖčÅ ą┤ąŠ ą┤ą▓čāčģ ą▒čāą┤ąĄčé C = 2^16 - |A ŌĆó B|.
ą¤ąŠą╗čāč湥ąĮąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé ą▒čāą┤ąĄčé ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ 0 .. 2^16 ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čćąĖčüąĄą╗ unsigned, ąĖ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ -2^15 .. 2^15-1 ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čćąĖčüąĄą╗ signed.
ąŁčéąĖą╝ ą┐ąŠą║ą░ąĘą░ąĮąŠ, ą║ą░ą║ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąŠ ą▓ąĮčāčéčĆąĖ čåąĄą╗ąŠčćąĖčüą╗ąĄąĮąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ ąĮą░ čÅąĘčŗą║ąĄ C. ąÉą╗ą│ąŠčĆąĖčéą╝ ą╝ąŠąČąĄčé ą▒čŗčéčī čĆą░čüčłąĖčĆąĄąĮ ą┤ą╗čÅ čāą╝ąĮąŠąČąĄąĮąĖčÅ 32-bit čćąĖčüąĄą╗ čü ą┐ąŠą╗čāč湥ąĮąĖąĄą╝ 32-bit čĆąĄąĘčāą╗čīčéą░čéą░.
ą×ą┐ąĄčĆą░čåąĖčÅ 16-bit * 16-bit = 24-bit
ążčāąĮą║čåąĖąŠąĮą░ą╗ ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ ąĖą╗ą╗čÄčüčéčĆąĖčĆčāąĄčéčüčÅ ąĮą░ čĆąĖčü. 4. ąöą╗čÅ 24-bit ą▓ąĄčĆčüąĖąĖ ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝ čāą╝ąĮąŠąČąĄąĮąĖčÅ čĆąĄąĘčāą╗čīčéą░čé ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮ ą▓ čĆąĄą│ąĖčüčéčĆą░čģ r18:r17:r16. ąÉą╗ą│ąŠčĆąĖčéą╝ ą┤ą░ąĄčé ą║ąŠčĆčĆąĄą║čéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé C = A ŌĆó B, ą║ąŠą│ą┤ą░ ąŠąĮ ą╝ąĄąĮčīčłąĄ 2^24 ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ unsigned, ąĖ ą╝ąĄąĮčīčłąĄ č湥ą╝ ┬▒2^23 ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ signed.
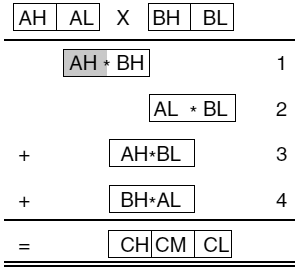
ąĀąĖčü. 4. 16-ą▒ąĖčéąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ, 24-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé.
ą×ą┐ąĄčĆą░čåąĖčÅ 16-bit * 16-bit = 32-bit
ą¤čĆąĖą╝ąĄčĆ 4 - ą▒ą░ąĘąŠą▓ąŠąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čāą╝ąĮąŠąČąĄąĮąĖčÅ čåąĄą╗čŗčģ čćąĖčüąĄą╗ 16-bit * 16-bit = 32-bit. ąØąĖąČąĄ ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą┐čĆąĖą╝ąĄčĆ, ą║ą░ą║ ą▓čŗąĘčŗą▓ą░čéčī ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čā čāą╝ąĮąŠąČąĄąĮąĖčÅ 16 x 16 = 32. ąŁč鹊 čéą░ą║ąČąĄ ą┐čĆąŠąĖą╗ą╗čÄčüčéčĆąĖčĆąŠą▓ą░ąĮąŠ ąĮą░ čĆąĖčü. 5.
1
2
3
4
5
|
ldi R23,HIGH(672)
ldi R22,LOW(672) ; ą¦ąĖčüą╗ąŠ 672 ąĘą░ą│čĆčāąČąĄąĮąŠ ą▓ ą┐ą░čĆčā r23:r22.
ldi R21,HIGH(1844)
ldi R20,LOW(184) ; ą¦ąĖčüą╗ąŠ 1844 ąĘą░ą│čĆčāąČąĄąĮąŠ ą▓ ą┐ą░čĆčā r21:r20.
call mul16x16_32 ; ąÆčŗąĘąŠą▓ ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ čāą╝ąĮąŠąČąĄąĮąĖčÅ.
|
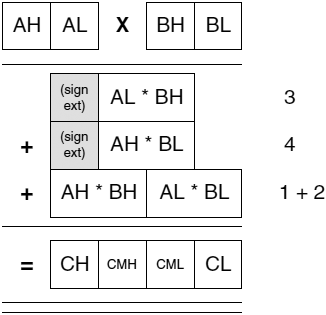
ąĀąĖčü. 5. 16-ą▒ąĖčéąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ, 32-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé.
32-bit čĆąĄąĘčāą╗čīčéą░čé čāą╝ąĮąŠąČąĄąĮąĖčÅ unsigned čćąĖčüąĄą╗ 672 ąĖ 1844 will č鹥ą┐ąĄčĆčī ą▒čāą┤ąĄčé čüąŠčģčĆą░ąĮąĄąĮ ą▓ čĆąĄą│ąĖčüčéčĆą░čģ R19:R18:R17:R16. ąĢčüą╗ąĖ ą▒čāą┤ąĄčé ą▓čŗąĘą▓ą░ąĮą░ muls16x16_32 ą▓ą╝ąĄčüč鹊 mul16x16_32, č鹊 ą▒čāą┤ąĄčé ą▓čŗą┐ąŠą╗ąĮąĄąĮąŠ čāą╝ąĮąŠąČąĄąĮąĖąĄ signed. ąĢčüą╗ąĖ ą▒čāą┤ąĄčé ą▓čŗąĘą▓ą░ąĮą░ mul16x16_16, č鹊 čĆąĄąĘčāą╗čīčéą░čé ą▒čāą┤ąĄčé ąĖą╝ąĄčéčī ą┤ą╗ąĖąĮčā č鹊ą╗čīą║ąŠ 16 ą▒ąĖčé, ąĖ čüąŠčģčĆą░ąĮąĄąĮ ą▓ ą┐ą░čĆčā čĆąĄą│ąĖčüčéčĆąŠą▓ R17:R16. ąöą╗čÅ ą┤ą░ąĮąĮąŠą│ąŠ ą┐čĆąĖą╝ąĄčĆą░ ąĘąĮą░č湥ąĮąĖą╣ čćąĖčüąĄą╗ 16-bit čĆąĄąĘčāą╗čīčéą░čé ą▒čāą┤ąĄčé ąĮąĄą║ąŠčĆčĆąĄą║č鹥ąĮ.
ą×ą┐ąĄčĆą░čåąĖčÅ 16-ą▒ąĖčé MAC (16-bit multiply-accumulate)

ąĀąĖčü. 6. 16-ą▒ąĖčéąĮąŠąĄ čāą╝ąĮąŠąČąĄąĮąĖąĄ, 32-ą▒ąĖčéąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé čü ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄą╝.
[ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ (Fractional Numbers)]
ąæąĄąĘąĘąĮą░ą║ąŠą▓čŗąĄ (unsigned) 8-ą▒ąĖčéąĮčŗąĄ ą┤čĆąŠą▒ąĮčŗąĄ (fractional) čćąĖčüą╗ą░ ąĖčüą┐ąŠą╗čīąĘčāčÄčé č乊čĆą╝ą░čé, ą│ą┤ąĄ ą┤ąŠą┐čāčüčéąĖą╝čŗ čćąĖčüą╗ą░ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ 0 .. < 2. ąæąĖčéčŗ 6 .. 0 ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅčÄčé ą┤čĆąŠą▒ąĮčāčÄ čćą░čüčéčī čćąĖčüą╗ą░, ąĖ ą▒ąĖčé 7 ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé čåąĄą╗čāčÄ čćą░čüčéčī čćąĖčüą╗ą░ (0 ąĖą╗ąĖ 1), čé. ąĄ. ą┐ąŠą╗čāčćą░ąĄčéčüčÅ č乊čĆą╝ą░čé 1.7. ąśąĮčüčéčĆčāą║čåąĖčÅ FMUL ą▓čŗą┐ąŠą╗ąĮčÅąĄčé čéčā ąČąĄ čüą░ą╝čāčÄ čĆą░ą▒ąŠčéčā, čćč鹊 ąĖ ąĖąĮčüčéčĆčāą║čåąĖčÅ MUL, ąĘą░ ąĖčüą║ą╗čÄč湥ąĮąĖąĄą╝ č鹊ą│ąŠ, čćč鹊 čĆąĄąĘčāą╗čīčéą░čé ą┐ąŠą╗čāčćą░ąĄčéčüčÅ čüą┤ą▓ąĖąĮčāčéčŗą╝ ą▓ą╗ąĄą▓ąŠ ąĮą░ 1 ą▒ąĖčé, čéą░ą║ čćč鹊 čüčéą░čĆčłąĖą╣ ą▒ą░ą╣čé ą┤ą▓čāčģą▒ą░ą╣čéąĮąŠą│ąŠ čĆąĄąĘčāą╗čīčéą░čéą░ ą▒čāą┤ąĄčé ąĖą╝ąĄčéčī č鹊čé ąČąĄ 1.7 č乊čĆą╝ą░čé, čćč鹊 ąĖ ąŠą┐ąĄčĆą░ąĮą┤čŗ (ą▓ą╝ąĄčüč鹊 č乊čĆą╝ą░čéą░ 2.6). ąśą╝ąĄą╣č鹥 ą▓ ą▓ąĖą┤čā, čćč鹊 ąĄčüą╗ąĖ čĆąĄąĘčāą╗čīčéą░čé čĆą░ą▓ąĄąĮ ąĖą╗ąĖ ą▒ąŠą╗čīčłąĄ 2, č鹊 ąŠąĮ ąĮąĄą║ąŠčĆčĆąĄą║č鹥ąĮ.
ąöą╗čÅ ą┐ąŠą╗ąĮąŠą│ąŠ ą┐ąŠąĮąĖą╝ą░ąĮąĖčÅ č乊čĆą╝ą░čéą░ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ ą┐ąŠą╗ąĄąĘąĮąŠ čüčĆą░ą▓ąĮąĖčéčī ąĄą│ąŠ čü č乊čĆą╝ą░č鹊ą╝ čåąĄą╗ąŠą│ąŠ čćąĖčüą╗ą░: čéą░ą▒ą╗ąĖčåą░ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą┤ą▓ą░ 8-bit č乊čĆą╝ą░čéą░ čćąĖčüąĄą╗ unsigned. ąöčĆąŠą▒ąĮčŗąĄ čćąĖčüą╗ą░ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed fractional), ą║ą░ą║ ąĖ čåąĄą╗čŗąĄ čćąĖčüą╗ą░ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed integer), ąĖčüą┐ąŠą╗čīąĘčāčÄčé ąĘąĮą░ą║ąŠą╝čŗą╣ č乊čĆą╝ą░čé čćąĖčüą╗ą░ čü ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖąĄą╝ ą┤ąŠ 2 (twoŌĆÖs complement format). ąÆ čŹč鹊ą╝ č乊čĆą╝ą░č鹥 ą╝ąŠą│čāčé ą▒čŗčéčī ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮčŗ čćąĖčüą╗ą░ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ -1 .. < 1.
| ąØąŠą╝ąĄčĆ ą▒ąĖčéą░ |
7 |
6 |
5 |
4 |
| ąŚąĮą░č湥ąĮąĖąĄ ą▒ąĖčé čåąĄą╗ąŠą│ąŠ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ąŠą│ąŠ čćąĖčüą╗ą░ (unsigned integer) |
27=128 |
26=64 |
25=32 |
24=16 |
| ąŚąĮą░č湥ąĮąĖąĄ ą▒ąĖčé čåąĄą╗ąŠą│ąŠ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ąŠą│ąŠ ą┤čĆąŠą▒ąĮąŠą│ąŠ čćąĖčüą╗ą░ (unsigned fractional) |
20=1 |
2-1=0.5 |
2-2=0.25 |
2-3=0.125 |
| ąØąŠą╝ąĄčĆ ą▒ąĖčéą░ |
3 |
2 |
1 |
0 |
| ąŚąĮą░č湥ąĮąĖąĄ ą▒ąĖčé čåąĄą╗ąŠą│ąŠ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ąŠą│ąŠ čćąĖčüą╗ą░ (unsigned integer) |
23=8 |
22=4 |
21=2 |
20=1 |
| ąŚąĮą░č湥ąĮąĖąĄ ą▒ąĖčé čåąĄą╗ąŠą│ąŠ ą▒ąĄąĘąĘąĮą░ą║ąŠą▓ąŠą│ąŠ ą┤čĆąŠą▒ąĮąŠą│ąŠ čćąĖčüą╗ą░ (unsigned fractional) |
2-4=0.0625 |
2-5=0.03125 |
2-6=0.015625 |
2-7=0.0078125 |
ąĢčüą╗ąĖ ą▒ą░ą╣čé 10110010 ąĖąĮč鹥čĆą┐čĆąĄčéąĖčĆąŠą▓ą░čéčī ą║ą░ą║ unsigned integer, č鹊 ąŠąĮ ą▒čāą┤ąĄčé čĆą░ą▓ąĄąĮ 128 + 32 + 16 + 2 = 178. ąśąĮą░č湥 ąŠąĮ ą╝ąŠąČąĄčé ą▒čŗčéčī ąĖąĮč鹥čĆą┐čĆąĄčéąĖčĆąŠą▓ą░ąĮ ą║ą░ą║ unsigned fractional, č鹊ą│ą┤ą░ ąŠąĮ čĆą░ą▓ąĄąĮ 1 + 0.25 + 0.125 + 0.015625 = 1.390625. ąĢčüą╗ąĖ ą┐ąŠą┤čĆą░ąĘčāą╝ąĄą▓ą░ąĄčéčüčÅ, čćč鹊 čŹč鹊 čåąĄą╗ąŠąĄ čćąĖčüą╗ąŠ signed integer, č鹊ą│ą┤ą░ ąŠąĮ čĆą░ą▓ąĄąĮ 178 - 256 = -122. ąĢčüą╗ąĖ ąČąĄ čŹč鹊 čćąĖčüą╗ąŠ signed fractional, č鹊 1.390625 - 2 = -0.609375.
ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ąĖąĮčüčéčĆčāą║čåąĖą╣ FMUL, FMULS ąĖ FMULSU ąĮąĄ ą┤ąŠą╗ąČąĮąŠ ą▒čŗčéčī ą▒ąŠą╗ąĄąĄ čüą╗ąŠąČąĮčŗą╝, č湥ą╝ ąĖąĮčüčéčĆčāą║čåąĖą╣ MUL, MULS ąĖ MULSU. ą×ą┤ąĮą░ą║ąŠ, ąŠą┤ąĮą░ ą┐ąŠč鹥ąĮčåąĖą░ą╗čīąĮą░čÅ ą┐čĆąŠą▒ą╗ąĄą╝ą░ čüąŠčüč鹊ąĖčé ą▓ ą┐čĆąĖčüą▓ą░ąĖą▓ą░ąĮąĖąĖ ąĘąĮą░č湥ąĮąĖą╣ ą┤čĆąŠą▒ąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄąĮąĮčŗčģ ą┐čĆąŠčüčéčŗą╝ čüą┐ąŠčüąŠą▒ąŠą╝. ąØą░ą┐čĆąĖą╝ąĄčĆ, ą┤čĆąŠą▒čī 0.75 (= 0.5 + 0.25) ą▒čāą┤ąĄčé 0110 0000, ąĄčüą╗ąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī 8 ą▒ąĖčé.
ąöą╗čÅ ą║ąŠąĮą▓ąĄčĆčéą░čåąĖąĖ ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮąŠą│ąŠ ą┤čĆąŠą▒ąĮąŠą│ąŠ čćąĖčüą╗ą░ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ 0 .. < 2 (ąĮą░ą┐čĆąĖą╝ąĄčĆ 1.8125) ą▓ č乊čĆą╝ą░čé, ąĖčüą┐ąŠą╗čīąĘčāąĄą╝čŗą╣ ą▓ AVR, ą┤ąŠą╗ąČąĄąĮ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčīčüčÅ čüą╗ąĄą┤čāčÄčēąĖą╣ ą░ą╗ą│ąŠčĆąĖčéą╝:
ąĢčüčéčī ą╗ąĖ "1" ą▓ čćąĖčüą╗ąĄ?
ąöą░, 1.8125 ą▒ąŠą╗čīčłąĄ ąĖą╗ąĖ čĆą░ą▓ąĮąŠ 1.
ąæą░ą╣čé č鹥ą┐ąĄčĆčī ą▒čāą┤ąĄčé 1xxxxxxx
ąśą╝ąĄąĄčéčüčÅ ą╗ąĖ ą▓ ąŠčüčéą░čéą║ąĄ 0.5?
0.8125/0.5 = 1.625
ąöą░, 1.625 ą▒ąŠą╗čīčłąĄ ąĖą╗ąĖ čĆą░ą▓ąĮąŠ 1.
ąæą░ą╣čé č鹥ą┐ąĄčĆčī ą▒čāą┤ąĄčé 11xxxxxx
ąśą╝ąĄąĄčéčüčÅ ą╗ąĖ ą▓ ąŠčüčéą░čéą║ąĄ 0.25?
0.625/0.5 = 1.25
ąöą░, 1.25 ą▒ąŠą╗čīčłąĄ ąĖą╗ąĖ čĆą░ą▓ąĮąŠ 1.
ąæą░ą╣čé č鹥ą┐ąĄčĆčī ą▒čāą┤ąĄčé 111xxxxx
ąśą╝ąĄąĄčéčüčÅ ą╗ąĖ ą▓ ąŠčüčéą░čéą║ąĄ 0.125?
0.25/0.5 = 0.5
ąØąĄčé, 0.5 ą╝ąĄąĮčīčłąĄ 1.
ąæą░ą╣čé č鹥ą┐ąĄčĆčī ą▒čāą┤ąĄčé 1110xxxx
ąśą╝ąĄąĄčéčüčÅ ą╗ąĖ ą▓ ąŠčüčéą░čéą║ąĄ 0.0625?
0.5/0.5 = 1
ąöą░, 1 ą▒ąŠą╗čīčłąĄ ąĖą╗ąĖ čĆą░ą▓ąĮąŠ 1.
ąæą░ą╣čé č鹥ą┐ąĄčĆčī ą▒čāą┤ąĄčé 11101xxx
ą¤ąŠčüą║ąŠą╗čīą║čā čā ąĮą░čü ąĮąĄ ąŠčüčéą░ą╗ąŠčüčī ą▒ąŠą╗čīčłąĄ ąŠčüčéą░čéą║ą░, ąŠčüčéą░ą╗čīąĮčŗąĄ 3 ą▒ąĖčéą░ ą▒čāą┤čāčé čĆą░ą▓ąĮčŗ 0, ąĖ ą║ąŠąĮąĄčćąĮčŗą╣ čĆąĄąĘčāą╗čīčéą░čé ą▒čāą┤ąĄčé čĆą░ą▓ąĄąĮ 11101000, ą│ą┤ąĄ 1 + 0.5 + 0.25 + 0.0625 = 1.8125.
ąöą╗čÅ ą║ąŠąĮą▓ąĄčĆčéą░čåąĖąĖ ąŠčéčĆąĖčåą░č鹥ą╗čīąĮąŠą│ąŠ ą┤čĆąŠą▒ąĮąŠą│ąŠ čćąĖčüą╗ą░ (negative fractional number) čüąĮą░čćą░ą╗ą░ ą┤ąŠą▒ą░ą▓čīč鹥 2 ą║ čćąĖčüą╗čā, ą░ ą┐ąŠč鹊ą╝ ąĖčüą┐ąŠą╗čīąĘčāą╣č鹥 č鹊čé ąČąĄ čüą░ą╝čŗą╣ ą░ą╗ą│ąŠčĆąĖčéą╝.
16-bit ą┤čĆąŠą▒ąĮčŗąĄ čćąĖčüą╗ą░ ąĖčüą┐ąŠą╗čīąĘčāčÄčé č鹊čé ąČąĄ č乊čĆą╝ą░čé, čćč鹊 ąĖ 8-bit ą┤čĆąŠą▒ąĮčŗąĄ čćąĖčüą╗ą░; čüčéą░čĆčłąĖąĄ 8 ą▒ąĖčé ąĖą╝ąĄčÄčé č鹊čćąĮąŠ čéą░ą║ąŠą╣ ąČąĄ č乊čĆą╝ą░čé, ą║ą░ą║ ąĖ čā ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ 8-bit. ą£ą╗ą░ą┤čłąĖąĄ 8 ą▒ąĖčé čāą▓ąĄą╗ąĖčćąĖą▓ą░čÄčé č鹊čćąĮąŠčüčéčī 8-bit č乊čĆą╝ą░čéą░; ąĄčüą╗ąĖ č乊čĆą╝ą░čé 8-bit ąĖą╝ąĄąĄčé č鹊čćąĮąŠčüčéčī of ┬▒2^-8, č鹊 č乊čĆą╝ą░čé 16-bit ąĖą╝ąĄąĄčé č鹊čćąĮąŠčüčéčī ┬▒2^-16. ąÉąĮą░ą╗ąŠą│ąĖčćąĮąŠ 32-bit ą┤čĆąŠą▒ąĮčŗąĄ čćąĖčüą╗ą░ čéą░ą║ąČąĄ čāą▓ąĄą╗ąĖčćąĖą▓ą░čÄčé č鹊čćąĮąŠčüčéčī 16-bit ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗. ą×ą▒čĆą░čéąĖč鹥 ą▓ąĮąĖą╝ą░ąĮąĖąĄ ąĮą░ ą▓ą░ąČąĮąŠąĄ ąŠčéą╗ąĖčćąĖąĄ ą╝ąĄąČą┤čā integer ąĖ fractional čćąĖčüą╗ą░ą╝ąĖ ą┐ąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÄ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ ą▒ą░ą╣čé: ą┤ą╗čÅ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ čāą▓ąĄą╗ąĖčćąĖą▓ą░ąĄčéčüčÅ č鹊čćąĮąŠčüčéčī, ą░ ą┤ą╗čÅ čåąĄą╗čŗčģ čćąĖčüąĄą╗ čāą▓ąĄą╗ąĖčćąĖą▓ą░ąĄčéčüčÅ ą┤ąĖą░ą┐ą░ąĘąŠąĮ.
ąÜą░ą║ ą▒čŗą╗ąŠ čāąČąĄ čāą┐ąŠą╝čÅąĮčāč鹊 čĆą░ąĮąĄąĄ, ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čćąĖčüąĄą╗ signed fractional ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ -1 .. < 1 ąĖą╝ąĄąĄčé ą┐čĆąĄąĖą╝čāčēąĄčüčéą▓ąŠ ą┐ąŠ čüčĆą░ą▓ąĮąĄąĮąĖčÄ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ integer: ą║ąŠą│ą┤ą░ čāą╝ąĮąŠąČą░čÄčéčüčÅ ą┤ą▓ą░ čćąĖčüą╗ą░ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ -1 .. < 1, č鹊 čĆąĄąĘčāą╗čīčéą░čé ą▒čāą┤ąĄčé ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ -1 .. 1, ąĖ ą▓ ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖąĖ (čüčéą░čĆčłąĖąĄ ą▒ą░ą╣čéčŗ) čĆąĄąĘčāą╗čīčéą░čéą░ ą╝ąŠą│čāčé ą▒čŗčéčī čüąŠčģčĆą░ąĮąĄąĮčŗ ą▓ č鹊ą╝ ąČąĄ ą║ąŠą╗ąĖč湥čüčéą▓ąĄ ą▒ą░ą╣čé, čćč鹊 ąĖ ą╝ąĮąŠąČąĖč鹥ą╗ąĖ, čü ąŠą┤ąĮąĖą╝ ą╗ąĖčłčī ąĖčüą║ą╗čÄč湥ąĮąĖąĄą╝: ą║ąŠą│ą┤ą░ ąŠą▒ą░ ą╝ąĮąŠąČąĖč鹥ą╗čÅ čĆą░ą▓ąĮčŗ -1, čĆąĄąĘčāą╗čīčéą░čé čāą╝ąĮąŠąČąĄąĮąĖčÅ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī čĆą░ą▓ąĄąĮ 1, ą┐ąŠ ą┐ąŠčüą║ąŠą╗čīą║čā čćąĖčüą╗ąŠ 1 ąĮąĄ ą╝ąŠąČąĄčé ą▒čŗčéčī ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąŠ ą▓ čŹč鹊ą╝ ą┤čĆąŠą▒ąĮąŠą╝ č乊čĆą╝ą░č鹥 čćąĖčüą╗ą░, č鹊 ąĖąĮčüčéčĆčāą║čåąĖčÅ FMULS ą┐ąŠą╝ąĄčüčéąĖčé ą▓ą╝ąĄčüč鹊 čŹč鹊ą│ąŠ čćąĖčüą╗ąŠ -1 ą▓ ą┐ą░čĆąĄ čĆąĄą│ąĖčüčéčĆąŠą▓ R1:R0. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ą┐ąŠą╗čīąĘąŠą▓ą░č鹥ą╗čī ą┤ąŠą╗ąČąĄąĮ ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ FMULS ą│ą░čĆą░ąĮčéąĖčĆąŠą▓ą░čéčī, čćč鹊 ą┐ąŠ ą║čĆą░ą╣ąĮąĄą╣ ą╝ąĄčĆąĄ čģąŠčéčÅ ą▒čŗ ąŠą┤ąĖąĮ ąĖąĘ ąŠą┐ąĄčĆą░ąĮą┤ąŠą▓ ąĮąĄ čĆą░ą▓ąĄąĮ -1. ąŻą╝ąĮąŠąČąĄąĮąĖąĄ 16-bit * 16-bit ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ čéą░ą║ąČąĄ ąĖą╝ąĄąĄčé čŹč鹊 ąŠą│čĆą░ąĮąĖč湥ąĮąĖąĄ.
ą¤čĆąĖą╝ąĄčĆ 5 ŌĆō ą▒ą░ąĘąŠą▓ąŠąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ čāą╝ąĮąŠąČąĄąĮąĖčÅ ą┤čĆąŠą▒ąĮčŗčģ čćąĖčüąĄą╗ čüąŠ ąĘąĮą░ą║ąŠą╝ (Signed Fractional) 8-bit * 8-bit = 16-bit
ąŁč鹊čé ą┐čĆąĖą╝ąĄčĆ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé ą║ąŠą┤ ą░čüčüąĄą╝ą▒ą╗ąĄčĆą░, ą║ąŠč鹊čĆčŗą╣ čćąĖčéą░ąĄčé ą▓čģąŠą┤ąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĖąĘ ą┐ąŠčĆčéą░ B, čāą╝ąĮąŠąČą░ąĄčé ąĄą│ąŠ ąĮą░ ą┤čĆąŠą▒ąĮčāčÄ ą║ąŠąĮčüčéą░ąĮčéčā (-0.625), ąĖ ąĘą░č鹥ą╝ čüąŠčģčĆą░ąĮčÅąĄčé čĆąĄąĘčāą╗čīčéą░čé ą▓ čĆąĄą│ąĖčüčéčĆąŠą▓ąŠą╣ ą┐ą░čĆąĄ R17:R16.
1
2
3
4
|
in r16,PINB ; ą¤čĆąŠčćąĖčéą░čéčī ąĘąĮą░č湥ąĮąĖąĄ ąĖąĘ ąĮąŠąČąĄą║ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░.
ldi r17,$B0 ; ąŚą░ą│čĆčāąĘąĖčéčī -0.625 ą▓ čĆąĄą│ąĖčüčéčĆ r17.
fmuls r16,r17 ; r1:r0 = r17 * r16
movw r17:r16,r1:r0 ; ą¤ąĄčĆąĄą╝ąĄčüčéąĖčéčī čĆąĄąĘčāą╗čīčéą░čé ą▓ r17:r16.
|
ą×ą▒čĆą░čéąĖč鹥 ą▓ąĮąĖą╝ą░ąĮąĖąĄ, čćč鹊 ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ąĖąĮčüčéčĆčāą║čåąĖą╣ FMULS (ąĖ FMUL) č鹊čćąĮąŠ čéą░ą║ ąČąĄ ą┐čĆąŠčüč鹊, ą║ą░ą║ ąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ MULS ąĖ MUL.
ą¤čĆąĖą╝ąĄčĆ 6 - ąŠą┐ąĄčĆą░čåąĖčÅ MAC
ą¤čĆąĖą╝ąĄčĆ ąĮąĖąČąĄ ąĖčüą┐ąŠą╗čīąĘčāąĄčé ą┤ą░ąĮąĮčŗąĄ ąĖąĘ ADC (ą░ąĮą░ą╗ąŠą│ąŠ-čåąĖčäčĆąŠą▓ąŠą╣ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░č鹥ą╗čī) ą┤ą╗čÅ ą┤ą░ąĮąĮčŗčģ ąŠą┐ąĄčĆą░čåąĖąĖ multiply accumulate (MAC, čüą╗ąŠąČąĄąĮąĖąĄ čü ąĮą░ą║ąŠą┐ą╗ąĄąĮąĖąĄą╝). ADC ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą┐čĆąĄą┤ą▓ą░čĆąĖč鹥ą╗čīąĮąŠ čüą║ąŠąĮčäąĖą│čāčĆąĖčĆąŠą▓ą░ąĮ, čćč鹊ą▒čŗ č乊čĆą╝ą░čé čĆąĄąĘčāą╗čīčéą░čéą░ ADC ą▒čŗą╗ čüąŠą▓ą╝ąĄčüčéąĖą╝ čü ą┤čĆąŠą▒ąĮčŗą╝ č乊čĆą╝ą░č鹊ą╝ čü ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖąĄą╝ ą┤ąŠ 2 (fractional twoŌĆÖs complement format). ąöą╗čÅ ATmega83/163 čŹč鹊 ąŠąĘąĮą░čćą░ąĄčé čāčüčéą░ąĮąŠą▓ą║čā ą▒ąĖčéą░ ADLAR ą▓ I/O čĆąĄą│ąĖčüčéčĆąĄ ADMUX, ąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠą│ąŠ ą║ą░ąĮą░ą╗ą░ (č鹊ą│ą┤ą░ čĆąĄąĘčāą╗čīčéą░čé ADC ą▒čāą┤ąĄčé ąĮąŠčĆą╝ą░ą╗ąĖąĘąŠą▓ą░ąĮ ą║ 1).
1
2
3
4
5
|
ldi r23,$62 ; ąŚą░ą│čĆčāąĘą║ą░ čüčéą░čĆčłąĄą│ąŠ ą▒ą░ą╣čéą░ ą┤čĆąŠą▒ąĖ 0.771484375
ldi r22,$C0 ; ąŚą░ą│čĆčāąĘą║ą░ ą╝ą╗ą░ą┤čłąĄą│ąŠ ą▒ą░ą╣čéą░ ą┤čĆąŠą▒ąĖ 0.771484375
in r20,ADCL ; ą¤ąŠą╗čāč湥ąĮąĖąĄ ą╝ą╗ą░ą┤čłąĄą│ąŠ ą▒ą░ą╣čéą░ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ADC
in r21,ADCH ; ą¤ąŠą╗čāč湥ąĮąĖąĄ čüčéą░čĆčłąĄą│ąŠ ą▒ą░ą╣čéą░ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ADC
call fmac16x16_32 ; ąÆčŗąĘąŠą▓ ą┐ąŠą┤ą┐čĆąŠą│čĆą░ą╝ą╝čŗ ą┤ą╗čÅ ą┤čĆąŠą▒ąĮąŠą╣ ąŠą┐ąĄčĆą░čåąĖąĖ MAC.
|
ąĀąĄą│ąĖčüčéčĆčŗ R19:R18:R17:R16 ą▒čāą┤čāčé ąĖąĮą║čĆąĄą╝ąĄąĮčéąĖčĆąŠą▓ą░ąĮčŗ čĆąĄąĘčāą╗čīčéą░č鹊ą╝ čāą╝ąĮąŠąČąĄąĮąĖčÅ 0.771484375 ąĮą░ ąĘąĮą░č湥ąĮąĖąĄ, čüčćąĖčéą░ąĮąĮąŠąĄ ąĖąĘ ADC (čŹč鹊 ą╝ąŠąČąĄčé ą▒čŗčéčī, ą║ ą┐čĆąĖą╝ąĄčĆčā, ą▓čŗą▒ąŠčĆą║ą░ ąĘą▓čāą║ąŠą▓ąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░, ąĮą░ą┤ ą║ąŠč鹊čĆčŗą╝ ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ čåąĖčäčĆąŠą▓ą░čÅ ąŠą▒čĆą░ą▒ąŠčéą║ą░). ąÆ čŹč鹊ą╝ ą┐čĆąĖą╝ąĄčĆąĄ čĆąĄąĘčāą╗čīčéą░čé ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ADC čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄčéčüčÅ ą║ą░ą║ ą┤čĆąŠą▒ąĮąŠąĄ čćąĖčüą╗ąŠ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed fraction number). ą£čŗ ą╝ąŠą│ą╗ąĖ ą▒čŗ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░čéčī ąĄą│ąŠ ą║ą░ą║ čåąĄą╗ąŠąĄ čćąĖčüą╗ąŠ čüąŠ ąĘąĮą░ą║ąŠą╝ (signed integer), ąĖ č鹊ą│ą┤ą░ ą┤ą╗čÅ čŹč鹊ą│ąŠ ąĮčāąČąĮąŠ ą▓čŗąĘą▓ą░čéčī mac16x16_32 ą▓ą╝ąĄčüč鹊 fmac16x16_32. ąÆ čŹč鹊ą╝ čüą╗čāčćą░ąĄ čćąĖčüą╗ąŠ 0.771484375 ą┤ąŠą╗ąČąĮąŠ ą▒čŗčéčī ąĘą░ą╝ąĄąĮąĄąĮąŠ ąĮą░ čåąĄą╗ąŠąĄ čćąĖčüą╗ąŠ (integer).
[ąÜąŠą╝ą╝ąĄąĮčéą░čĆąĖąĖ ą║ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅą╝]
ąÆčüąĄ 16-bit * 16-bit = 32-bit čäčāąĮą║čåąĖąĖ, čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąĮčŗąĄ ąĘą┤ąĄčüčī, ąĮą░čćąĖąĮą░čÄčé čĆą░ą▒ąŠčéčā čü ąŠčćąĖčüčéą║ąĖ čĆąĄą│ąĖčüčéčĆą░ R2, ą║ąŠč鹊čĆčŗą╣ ą┐čĆąŠčüč鹊 ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą║ą░ą║ "dummy" čĆąĄą│ąĖčüčéčĆ (ąĘą░ą│ą╗čāčłą║ą░) ą▓ ąŠą┐ąĄčĆą░čåąĖčÅčģ "čüą╗ąŠąČąĄąĮąĖąĄ čü ą┐ąĄčĆąĄąĮąŠčüąŠą╝" (add with carry, ADC) ąĖ "ą▓čŗčćąĖčéą░ąĮąĖąĄ čü ąĘą░čæą╝ąŠą╝" (subtract with carry, SBC). ąŁčéąĖ ąŠą┐ąĄčĆą░čåąĖąĖ ąĮąĄ ąĖąĘą╝ąĄąĮčÅčÄčé ąĘąĮą░č湥ąĮąĖąĄ čĆąĄą│ąĖčüčéčĆą░ R2. ąĢčüą╗ąĖ čĆąĄą│ąĖčüčéčĆ R2 ąĮąĄ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą│ą┤ąĄ-ąĮąĖą▒čāą┤čī ą▓ ą║ąŠą┤ąĄ, č鹊 ąĮąĄ ąĮčāąČąĮąŠ ąŠčćąĖčēą░čéčī ą║ą░ąČą┤čŗą╣ čĆą░ąĘ R2 ą┐čĆąĖ ą▓čŗąĘąŠą▓ąĄ čŹčéąĖčģ čäčāąĮą║čåąĖą╣, ąĮąŠ č鹊ą╗čīą║ąŠ ąŠą┤ąĖąĮ čĆą░ąĘ ą┐ąĄčĆąĄą┤ ą┐ąĄčĆą▓čŗą╝ ą▓čŗąĘąŠą▓ąŠą╝ ąŠą┤ąĮąŠą╣ ąĖąĘ čŹčéąĖčģ čäčāąĮą║čåąĖą╣.
[ąĪčüčŗą╗ą║ąĖ]
1. AVR201: Using the AVR® Hardware Multiplier site:atmel.com.
2. ążą░ą╣ą╗ AVR201.asm, ą┤ąŠą║čāą╝ąĄąĮčéą░čåąĖčÅ.
3. AVR223: Digital Filters with AVR (čåąĖčäčĆąŠą▓čŗąĄ čäąĖą╗čīčéčĆčŗ ąĮą░ AVR). |
