|
ąŚą┤ąĄčüčī ą┐čĆąĖą▓ąĄą┤ąĄąĮą░ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ ą┐čĆąŠčüč鹊ą│ąŠ čåąĖčäčĆąŠą▓ąŠą│ąŠ čäąĖą╗čīčéčĆą░ (ą┐ąĄčĆąĄą▓ąŠą┤ čüčéą░čéčīąĖ [1]), ą║ąŠč鹊čĆčŗą╣ čāą┤ąŠą▒ąĮąŠ ą┐čĆąĖą╝ąĄąĮčÅčéčī čü ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░ą╝ąĖ ą┤ą╗čÅ ąŠčĆą│ą░ąĮąĖąĘą░čåąĖąĖ čüąĄąĮčüąŠčĆąĮąŠą│ąŠ ą▓ą▓ąŠą┤ą░. ąŁč鹊 čéą░ą║ ąĮą░ąĘčŗą▓ą░ąĄą╝čŗą╣ čäąĖą╗čīčéčĆ čŹą║čüą┐ąŠąĮąĄąĮčåąĖą░ą╗čīąĮąŠą│ąŠ čüą║ąŠą╗čīąĘčÅčēąĄą│ąŠ čüčĆąĄą┤ąĮąĄą│ąŠ (Exponential Moving Average, EMA [2], ą║ąŠč鹊čĆčŗą╣ čéą░ą║ąČąĄ ą▓ č鹥čĆą╝ąĖąĮąŠą╗ąŠą│ąĖąĖ DSP ąĮą░ąĘčŗą▓ą░čÄčé čäąĖą╗čīčéčĆąŠą╝ čü ą▒ąĄčüą║ąŠąĮąĄčćąĮąŠą╣ ąĖą╝ą┐čāą╗čīčüąĮąŠą╣ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąŠą╣, ąæąśąź-čäąĖą╗čīčéčĆąŠą╝ (Infinite-Impulse Response, IIR). ąöąŠčüč鹊ąĖąĮčüčéą▓ąŠ EMA-čäąĖą╗čīčéčĆą░ ą▓ č鹊ą╝, čćč鹊 ąŠąĮ čéčĆąĄą▒čāąĄčé čüąŠą▓čüąĄą╝ ąĮąĄą╝ąĮąŠą│ąŠ ą▓čŗčćąĖčüą╗ąĖč鹥ą╗čīąĮąŠą╣ ą╝ąŠčēąĮąŠčüčéąĖ ąĖ ąĮąĄą╝ąĮąŠą│ąŠ ąŠą┐ąĄčĆą░čéąĖą▓ąĮąŠą╣ ą┐ą░ą╝čÅčéąĖ, čćč鹊 ąŠčüąŠą▒ąĄąĮąĮąŠ ą▓ą░ąČąĮąŠ ą┤ą╗čÅ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆąŠą▓.
[ą¦č鹊 čéą░ą║ąŠąĄ čäąĖą╗čīčéčĆ?]
ążąĖą╗čīčéčĆčŗ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ ą┤ą╗čÅ čāą┤ą░ą╗ąĄąĮąĖčÅ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĮčŗčģ čćą░čüč鹊čé ąĖąĘ čüąĖą│ąĮą░ą╗ą░. ąöą░ą▓ąĮčŗą╝ ą┤ą░ą▓ąĮąŠ ąöąČąŠąĘąĄčä ążčāčĆčīąĄ ą┤ąŠą│ą░ą┤ą░ą╗čüčÅ, čćč鹊 ą╗čÄą▒ąŠą╣ čüąĖą│ąĮą░ą╗ ą╝ąŠąČąĮąŠ ą┐čĆąĄą┤čüčéą░ą▓ąĖčéčī čüčāą╝ą╝ąŠą╣ ą┐čĆąŠčüčéčŗčģ čüąĖąĮčāčüąŠąĖą┤ą░ą╗čīąĮčŗčģ čüąĖą│ąĮą░ą╗ąŠą▓ čü čĆą░ąĘąĮčŗą╝ąĖ čćą░čüč鹊čéą░ą╝ąĖ. ąŁč鹊 ą┤ą░ą╗ąŠ ąĖąĮąČąĄąĮąĄčĆą░ą╝ ą╝ąŠčēąĮčŗą╣ ąĖąĮčüčéčĆčāą╝ąĄąĮčéą░čĆąĖą╣ (ąĮą░ą┐ąŠą┤ąŠą▒ąĖąĄ ą▒čŗčüčéčĆąŠą│ąŠ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ążčāčĆčīąĄ, ąæą¤ąż), ąĖ ą╝čŗ čüą┐ąŠčüąŠą▒ąĮčŗ ą┐ąŠąĮąĖą╝ą░čéčī ąĖ čĆą░ąĘčĆą░ą▒ą░čéčŗą▓ą░čéčī čäąĖą╗čīčéčĆčŗ. ąöą╗čÅ ą┐čĆąĖą╝ąĄčĆą░ čĆąĖčüčāąĮąŠą║ ąĮąĖąČ ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé čäąĖą╗čīčéčĆ ąĮąĖąĘą║ąĖčģ čćą░čüč鹊čé, ążąØą¦. ą×ąĮ ą┐čĆąŠą┐čāčüą║ą░ąĄčé ąĮąĖąĘą║ąĖąĄ čćą░čüč鹊čéčŗ ąĖ ą▒ą╗ąŠą║ąĖčĆčāąĄčé ą▓čŗčüąŠą║ąĖąĄ čćą░čüč鹊čéčŗ.
ąÉąĮą░ą╗ąŠą│ąŠą▓čŗąĄ čäąĖą╗čīčéčĆčŗ čģą░čĆą░ą║č鹥čĆąĖąĘčāčÄčéčüčÅ čćą░čüč鹊čéąĮąŠą╣ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąŠą╣, čé. ąĄ. ą║ą░ą║ ąŠąĮąĖ ąŠčüą╗ą░ą▒ą╗čÅčÄčé ąĖą╗ąĖ ą┐čĆąŠą┐čāčüą║ą░čÄčé čĆą░ąĘąĮčŗąĄ čćą░čüč鹊čéčŗ (magnitude response, ąĖą╗ąĖ ąÉą¦ąź) ąĖ čüą┤ą▓ąĖą│ąŠą╝ čäą░ąĘčŗ čüąĖą│ąĮą░ą╗ą░ (phase response, ążą¦ąź). ąöą╗čÅ ą┐ąŠą║ą░ąĘą░ąĮąĮąŠą╣ ą▓čŗčłąĄ čüčģąĄą╝čŗ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ą░ ąÉą¦ąź čüą╗ąĄą┤čāčÄčēą░čÅ (čŹč鹊 čäąĖą╗čīčéčĆ ąĮąĖąĘą║ąĖčģ čćą░čüč鹊čé, ążąØą¦):
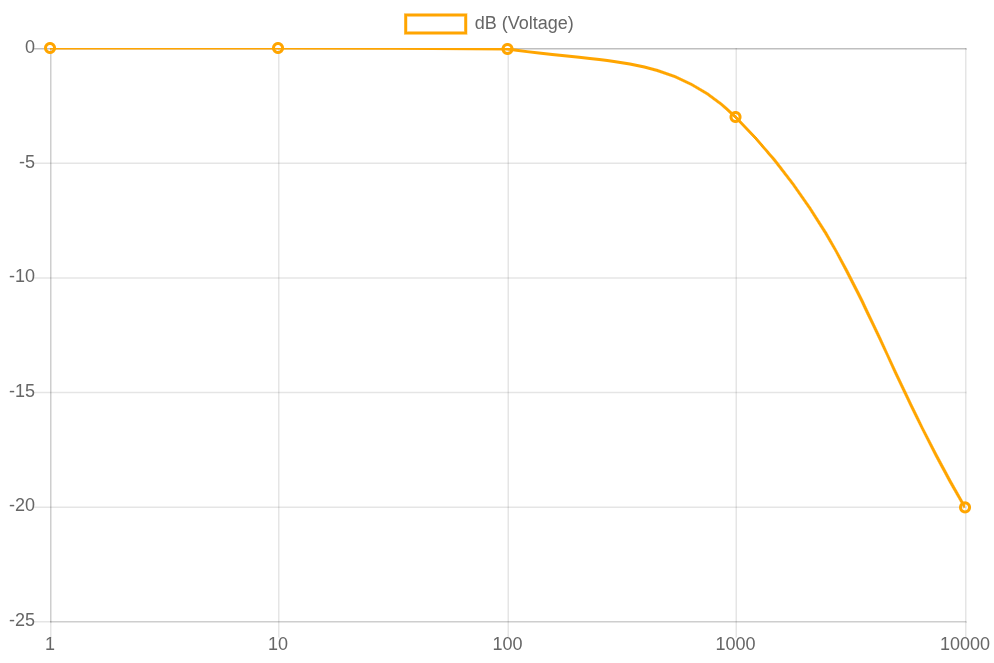
ą¤ąŠ ąŠčüąĖ x ąĮą░ čŹč鹊ą╝ ą│čĆą░čäąĖą║ąĄ čłą║ą░ą╗ą░ ą╗ąŠą│ą░čĆąĖčäą╝ąĖč湥čüą║ą░čÅ (ą║ą░ąČą┤ą░čÅ ąŠčéą╝ąĄčéą║ą░ ą┐ąŠ ą▓ąĄčüčā ą▓ ą┤ąĄčüčÅčéčī čĆą░ąĘ ą▒ąŠą╗čīčłąĄ ą┐čĆąĄą┤čŗą┤čāčēąĄą╣). ą¤ąŠ ąŠčüąĖ y čłą║ą░ą╗ą░ ą▓ ą┤ąĄčåąĖą▒ąĄą╗ą░čģ dBV [3] (ą╗ąŠą│ą░čĆąĖčäą╝ąĖč湥čüą║ąŠąĄ ąĖąĘą╝ąĄčĆąĄąĮąĖąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ). ą¦ą░čüč鹊čéą░ čüčĆąĄąĘą░ čā čŹč鹊ą│ąŠ čäąĖą╗čīčéčĆą░ 160 ąōčå, ą║ąŠą│ą┤ą░ čüąŠ ą▓čģąŠą┤ą░ ąĮą░ ą▓čŗčģąŠą┤ ą┐ąĄčĆąĄą┤ą░ąĄčéčüčÅ ą╝ąĄąĮčīčłąĄ ą┐ąŠą╗ąŠą▓ąĖąĮčŗ ą╝ąŠčēąĮąŠčüčéąĖ ąĮą░ čŹč鹊ą╣ čćą░čüč鹊č鹥 (čŹč鹊 čéą░ą║ąČąĄ č鹊čćą║ą░, ąĮą░ ą║ąŠč鹊čĆąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮą░ ą▓čŗčģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░ čüčéą░ąĮąŠą▓ąĖčéčüčÅ ą┐ąŠ čāčĆąŠą▓ąĮčÄ -3dBV).
ą¤ąŠą║ą░ąĘą░ąĮąĮčŗą╣ ą▓čŗčłąĄ ążąØą¦ ąŠčéą╗ąĖčćąĮąŠ ą┐ąŠą┤čģąŠą┤ąĖčé ą┤ą╗čÅ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ čüąĖą│ąĮą░ą╗ąŠą▓, ą┐ąŠą┤ą╗ąĄąČą░čēąĖčģ ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ ąÉą”ą¤ ą╝ąĖą║čĆąŠą║ąŠąĮčéčĆąŠą╗ą╗ąĄčĆą░. ąÉą”ą¤ ąĘą░čģą▓ą░čéčŗą▓ą░ąĄčé č鹊ą╗čīą║ąŠ čćą░čüč鹊čéčŗ, ą║ąŠč鹊čĆčŗąĄ čüąŠčüčéą░ą▓ą╗čÅčÄčé ą┤ąŠ ą┐ąŠą╗ąŠą▓ąĖąĮčŗ čćą░čüč鹊čéčŗ ą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ. ąĢčüą╗ąĖ ąÉą”ą¤ ą┤ąĄą╗ą░ąĄčé 320 ąŠčéčüč湥č鹊ą▓ ą▓ čüąĄą║čāąĮą┤čā, čüąĖą│ąĮą░ą╗ ą┤ąŠą╗ąČąĄąĮ ą▒čŗčéčī ą┐ąŠ čćą░čüč鹊č鹥 ą╝ąĄąĮčīčłąĄ 160 ąōčå. ąĢčüą╗ąĖ čüąĖą│ąĮą░ą╗ ąĮąĄ čäąĖą╗čīčéčĆčāąĄčéčüčÅ ą▓čŗčłąĄ 160 ąōčå, čŹčéąĖ ą▒ąŠą╗ąĄąĄ ą▓čŗčüąŠą║ąĖąĄ čćą░čüč鹊čéčŗ ą▒čāą┤čāčé ą┐ąĄčĆąĄą║čĆčŗą▓ą░čéčīčüčÅ čü ą▒ąŠą╗ąĄąĄ ąĮąĖąĘą║ąĖą╝ąĖ čćą░čüč鹊čéą░ą╝ąĖ. ąŁč鹊 č乥ąĮąŠą╝ąĄąĮ, ąĖąĘą▓ąĄčüčéąĮčŗą╣ ą║ą░ą║ ą░ą╗ąĖą░čüąĖąĮą│, ąŠąĮ čÅą▓ą╗čÅąĄčéčüčÅ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąĖą╝ ą┐ąŠą▒ąŠčćąĮčŗą╝ čŹčäč乥ą║č鹊ą╝ čåąĖčäčĆąŠą▓ąŠą╣ ą▓čŗą▒ąŠčĆą║ąĖ čüąĖą│ąĮą░ą╗ą░.
ą”ąĖčäčĆąŠą▓čŗąĄ čäąĖą╗čīčĆčŗ. ąŁč鹊 čäąĖą╗čīčéčĆčŗ, čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąĮčŗąĄ ąĮą░ ąŠčüąĮąŠą▓ąĄ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąĖčģ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ ą▓ą╝ąĄčüč鹊 ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ą░ąĮą░ą╗ąŠą│ąŠą▓čŗčģ ą║ąŠą╝ą┐ąŠąĮąĄąĮč鹊ą▓. ąśčģ čĆąĄą░ą╗ąĖąĘą░čåąĖčÅ ą┐ąŠą┤čĆą░ąĘčāą╝ąĄą▓ą░ąĄčé ą┐čĆąĄą┤ą▓ą░čĆąĖč鹥ą╗čīąĮčāčÄ ąŠčåąĖčäčĆąŠą▓ą║čā čüąĖą│ąĮą░ą╗ą░ čü ą┐ąŠą╝ąŠčēčīčÄ ąÉą”ą¤, ąĖ ą┐ąŠčüą╗ąĄą┤čāčÄčēčāčÄ ą▓čŗčćąĖčüą╗ąĖč鹥ą╗čīąĮčāčÄ ąŠą▒čĆą░ą▒ąŠčéą║čā ą┤ą░ąĮąĮčŗčģ čüąĖą│ąĮą░ą╗ą░ ą┐čĆąŠą│čĆą░ą╝ą╝ąĮčŗą╝ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą╝. ąĪčāčēąĄčüčéą▓čāčÄčé 2 ąŠčüąĮąŠą▓ąĮčŗčģ čĆą░ąĘąĮąŠą▓ąĖą┤ąĮąŠčüčéąĖ čäąĖą╗čīčéčĆąŠą▓: FIR ąĖ IIR.
FIR. Finite Impulse Response (FIR) čäąĖą╗čīčéčĆčŗ ąĖčüą┐ąŠą╗čīąĘčāčÄčé ą║ąŠąĮąĄčćąĮąŠąĄ ą║ąŠą╗ąĖč湥čüčéą▓ąŠ ą▓čŗą▒ąŠčĆąŠą║ ą┤ą╗čÅ ą│ąĄąĮąĄčĆą░čåąĖąĖ ąĖąĘ ąĮąĖčģ ą▓čŗčģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░. ą¤čĆąĖą╝ąĄčĆ ą┐čĆąŠčüč鹊ą│ąŠ FIR ążąØą¦ - čüą║ąŠą╗čīąĘčÅčēąĖą╣ čāčüčĆąĄą┤ąĮčÅčÄčēąĖą╣ čäąĖą╗čīčéčĆ (simple moving average). ąóą░ą║ąĖąĄ čäąĖą╗čīčéčĆčŗ ąĮąĄ č鹊ą╗čīą║ąŠ čüčĆąĄąĘą░čÄčé ą▓čŗčüąŠą║ąĖąĄ čćą░čüč鹊čéčŗ ą▒ą╗ą░ą│ąŠą┤ą░čĆčÅ "čüą│ą╗ą░ąČąĖą▓ą░ąĮąĖčÄ", ąĮąŠ čéą░ą║ąČąĄ ą╝ąŠą│čāčé ą┐ąŠą▓čŗčüąĖčéčī čĆą░ąĘčĆčÅą┤ąĮąŠčüčéčī ą░ąĮą░ą╗ąŠą│ąŠ-čåąĖčäčĆąŠą▓ąŠą│ąŠ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ [4]. ąÆ ąĮą░ąĘą▓ą░ąĮąĖąĖ FIR-čäąĖą╗čīčéčĆą░ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ čüą╗ąŠą▓ąŠ "finite", ą┐ąŠč鹊ą╝čā čćč鹊 ą▓čŗčģąŠą┤ čäąĖą╗čīčéčĆą░ ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ ą┐ąŠ ą║ąŠąĮąĄčćąĮąŠą╝čā ą║ąŠą╗ąĖč湥čüčéą▓čā ą▓čģąŠą┤ąĮčŗčģ ą▓čŗą▒ąŠčĆąŠą║. ąØą░ą┐čĆąĖą╝ąĄčĆ, 12-č鹊č湥čćąĮčŗą╣ čäąĖą╗čīčéčĆ čüą║ąŠą╗čīąĘčÅčēąĄą│ąŠ čüčĆąĄą┤ąĮąĄą│ąŠ čüčāą╝ą╝ąĖčĆčāąĄčé 12 ą┐ąŠčüą╗ąĄą┤ąĮąĖčģ ą▓čŗą▒ąŠčĆąŠą║, ą░ ąĘą░č鹥ą╝ ą┤ąĄą╗ąĖčé ąĖčģ ąĮą░ 12.
ąÆčŗčģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗ ąæąśąź-čäąĖą╗čīčéčĆąŠą▓ (IIR) ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ (ą▓ą┐ą╗ąŠčéčī ą┤ąŠ) ą▒ąĄčüą║ąŠąĮąĄčćąĮčŗą╝ čćąĖčüą╗ąŠą╝ ą▓čģąŠą┤ąĮčŗčģ ą▓čŗą▒ąŠčĆąŠą║.
IIR. Infinite Impulse Response (IIR) čäąĖą╗čīčéčĆčŗ čŹč鹊 čéą░ą║ąŠą╣ čéąĖą┐ čåąĖčäčĆąŠą▓čŗčģ čäąĖą╗čīčéčĆąŠą▓, čā ą║ąŠč鹊čĆčŗčģ ąĮą░ ą▓čŗčģąŠą┤ ą▓ą╗ąĖčÅąĄčé ą▒ąĄčüą║ąŠąĮąĄčćąĮąŠąĄ ą║ąŠą╗ąĖč湥čüčéą▓ąŠ ą▓čģąŠą┤ąĮčŗčģ ą▓čŗą▒ąŠčĆąŠą║ čüąĖą│ąĮą░ą╗ą░. Exponential moving average (EMA) čäąĖą╗čīčéčĆ ąŠčéąĮąŠčüąĖčéčüčÅ ą║ IIR ążąØą¦ čäąĖą╗čīčéčĆą░ą╝.
EMA. Exponential moving average (EMA) čäąĖą╗čīčéčĆ ą┤ą╗čÅ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ čüčĆąĄą┤ąĮąĄą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ ą┐čĆąĖą╝ąĄąĮčÅąĄčé 菹║čüą┐ąŠąĮąĄąĮčåąĖą░ą╗čīąĮąŠ ąĖąĘą╝ąĄąĮčÅčÄčēčāčÄčüčÅ ą▓ąĄą╗ąĖčćąĖąĮčā ą║ ą║ą░ąČą┤ąŠą╣ ą▓čŗą▒ąŠčĆą║ąĄ ą▓čģąŠą┤ąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░. ąźąŠčéčÅ čŹč鹊 ąĘą▓čāčćąĖčé ą║ą░ą║ čćč鹊-č鹊 čüą╗ąČąĮąŠąĄ, ąĮąŠ ąĮą░ ą┐čĆą░ą║čéąĖą║ąĄ ą░ą╗ą│ąŠčĆąĖčéą╝ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ą┐ąŠą╗čāčćą░ąĄčéčüčÅ ą┐čĆąŠčüč鹊ą╣, ąĖ ąĮą░ čÅąĘčŗą║ąĄ DSP ąĮą░ąĘčŗą▓ą░ąĄčéčüčÅ "čāčĆą░ą▓ąĮąĄąĮąĖąĄą╝ čĆą░ąĘąĮąŠčüčéąĖ" (difference equation):
y[n]=y[nŌłÆ1]Ōŗģ(1ŌłÆ╬▒)+x[n]Ōŗģ╬▒
ąŚą┤ąĄčüčī:
y čŹč鹊 ą▓čŗčģąŠą┤ čäąĖą╗čīčéčĆą░
n ąŠą▒ąŠąĘąĮą░čćą░ąĄčé ąĮąŠą╝ąĄčĆ ą▓čŗą▒ąŠčĆą║ąĖ čüąĖą│ąĮą░ą╗ą░
x ą▓čģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗
╬▒ ą║ąŠąĮčüčéą░ąĮčéą░, ąŠčé ą║ąŠč鹊čĆąŠą╣ ąĘą░ą▓ąĖčüąĖčé čćą░čüč鹊čéą░ čüčĆąĄąĘą░ čäąĖą╗čīčéčĆą░ (ą╝ąŠąČąĄčé ą▒čŗčéčī ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ąŠčé 0 ą┤ąŠ 1).
ąØą░ čüą╗ąĄą┤čāčÄčēąĄą╝ čĆąĖčüčāąĮą║ąĄ ą┐ąŠą║ą░ąĘą░ąĮą░ ąÉą¦ąź čäąĖą╗čīčéčĆą░ ą┤ą╗čÅ ╬▒=0.5 ąĖ čćą░čüč鹊čéčŗ ą┤ąĖčüą║ąĄčéąĖąĘą░čåąĖąĖ 1000 ąōčå.
ąŚąĮą░č湥ąĮąĖčÅ ą┐ąŠ ąŠčüąĖ y čāą║ą░ąĘą░ąĮčŗ ą▓ ą┤ąĄčåąĖą▒ąĄą╗ą░čģ, ą┐ąŠ ąŠčüąĖ x čłą║ą░ą╗ą░ ą╗ąŠą│ą░čĆąĖčäą╝ąĖč湥čüą║ą░čÅ ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ąŠčé 0.5 ą┤ąŠ 500 ąōčå.
EMA-čäąĖą╗čīčéčĆ ąŠčéą╗ąĖčćąĮąŠ ą┐ąŠą┤čģąŠą┤ąĖčé ą┤ą╗čÅ ą▓čüčéčĆą░ąĖą▓ą░ąĄą╝čŗčģ čĆąĄčłąĄąĮąĖą╣ ą┐ąŠ 2 ą┐čĆąĖčćąĖąĮą░ą╝. ąÆąŠ-ą┐ąĄčĆą▓čŗčģ, ą┐čĆąŠčüč鹊 ąĮą░čüčéčĆąŠąĖčéčī čćą░čüč鹊čéčā čüčĆąĄąĘą░. ąŻą╝ąĄąĮčīčłąĄąĮąĖąĄ ąĘąĮą░č湥ąĮąĖčÅ ╬▒ ą┐ąŠąĮąĖąČą░ąĄčé čćą░čüč鹊čéčā čüčĆąĄąĘą░ čäąĖą╗čīčéčĆą░, ą▓čŗ ą╝ąŠąČąĄč鹥 čāą▓ąĖą┤ąĄčéčī čĆą░ąĘąĮąĖčåčā ąĮą░ čüą╗ąĄą┤čāčÄčēąĄą╣ ą║ą░čĆčéąĖąĮą║ąĄ, ą│ą┤ąĄ ╬▒=0.1.
ąÆąŠ-ą▓č鹊čĆčŗčģ, EMA ą┐čĆąŠčüč鹊 ą║ąŠą┤ąĖčĆčāąĄčéčüčÅ ąĖ čéčĆąĄą▒čāąĄčé ą┤ą╗čÅ čüąĄą▒čÅ čüąŠą▓čüąĄą╝ ąĮąĄą╝ąĮąŠą│ąŠ čĆąĄčüčāčĆčüąŠą▓ ą┐čĆąŠčåąĄčüčüąŠčĆą░ (ą▓čŗčćąĖčüą╗ąĖč鹥ą╗čīąĮąŠą╣ ą╝ąŠčēąĮąŠčüčéąĖ ąĖ ą┐ą░ą╝čÅčéąĖ). ąśčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ 2 ąŠą┐ąĄčĆą░čåąĖąĖ čāą╝ąĮąŠąČąĄąĮąĖčÅ ąĖ ąŠą┤ąĮą░ ąŠą┐ąĄčĆą░čåąĖčÅ čüą╗ąŠąČąĄąĮąĖčÅ ą┤ą╗čÅ ą║ą░ąČą┤ąŠą│ąŠ ą▓čŗą▓ąŠą┤ą░, ąŠą┐ąĄčĆą░čåąĖąĖ ą┤ą╗čÅ ąŠą║čĆčāą│ą╗ąĄąĮąĖčÅ čćąĖčüąĄą╗ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ ąĘą░ą┐čÅč鹊ą╣ ąĖą│ąĮąŠčĆąĖčĆčāčÄčéčüčÅ. ąóąŠą╗čīą║ąŠ čüą░ą╝ą░čÅ ą┐ąŠčüą╗ąĄą┤ąĮčÅčÅ ą▓čŗą▒ąŠčĆą░ ą┤ąŠą╗ąČąĮą░ ą▒čŗčéčī čüąŠčģčĆą░ąĮąĮą░ ą▓ RAM. ąŁč鹊 čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ą╝ąĄąĮčīčłąĄ, č湥ą╝ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą┐čĆąŠčüč鹊ą│ąŠ čäąĖą╗čīčéčĆą░ čüą║ąŠą╗čīąĘčÅčēąĄą│ąŠ čüčĆąĄą┤ąĮąĄą│ąŠ čü N č鹊čćą║ą░ą╝ąĖ, ą║ąŠč鹊čĆčŗą╣ čéčĆąĄą▒čāąĄčé N ąŠą┐ąĄčĆą░čåąĖą╣ čāą╝ąĮąŠąČąĄąĮąĖčÅ ąĖ čüą╗ąŠąČąĄąĮąĖčÅ, ą░ čéą░ą║ąČąĄ N ą▓čŗą▒ąŠčĆąŠą║ ą┤ą╗čÅ čüąŠčģčĆą░ąĮąĄąĮąĖčÅ ą▓ ą×ąŚąŻ. ąĪą╗ąĄą┤čāčÄčēąĖą╣ ą║ąŠą┤ čĆąĄą░ą╗ąĖąĘčāąĄčé čäąĖą╗čīčéčĆ EMA, ąĖčüą┐ąŠą╗čīąĘčāčÅ 32-čĆą░ąĘčĆčÅą┤ąĮčāčÄ ą╝ą░č鹥ą╝ą░čéąĖą║čā čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮąŠą╣ č鹊čćą║ąŠą╣.
#define DSP_EMA_I32_ALPHA(x) ( (uint16_t)(x * 65535) )
int32_t dsp_ema_i32 (int32_t in, int32_t average, uint16_t alpha )
{
if ( alpha == 65535 )
return in;
int64_t tmp0;
tmp0 = (int64_t)in * (alpha+1) + average * (65536 - alpha);
return (int32_t)((tmp0 + 32768) / 65536);
}
ą¤čĆąĖą╝ąĄčĆ, ą║ą░ą║ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī čäčāąĮą║čåąĖčÄ čäąĖą╗čīčéčĆą░ dsp_ema_i32:
int32_t my_avg_func(void)
{
static int32_t average = 0;
int32_t adc_value;
adc_value = read_the_adc_value();
average = dsp_ema_i32(adc_value, average, DSP_EMA_I32_ALPHA(0.1));
return average;
}
[ąĪčüčŗą╗ą║ąĖ]
1. An Easy-to-Use Digital Filter site:blog.stratifylabs.co.
2. ąŁą║čüą┐ąŠąĮąĄąĮčåąĖą░ą╗čīąĮčŗąĄ čäąĖą╗čīčéčĆčŗ čüą║ąŠą╗čīąĘčÅčēąĄą│ąŠ čüčĆąĄą┤ąĮąĄą│ąŠ.
3. ą¦č鹊 čéą░ą║ąŠąĄ ą┤ąĄčåąĖą▒ąĄą╗?
4. ąŻą╗čāčćčłąĄąĮąĖąĄ ąŠčåąĖčäčĆąŠą▓ą║ąĖ čü ą┐ąŠą╝ąŠčēčīčÄ ą┐ąĄčĆąĄą┤ąĖčüą║čĆąĄčéąĖąĘą░čåąĖąĖ ąĖ čāčüčĆąĄą┤ąĮąĄąĮąĖčÅ.
5. ąÉą╗ą│ąŠčĆąĖčéą╝ ą╝ąĄą┤ąĖą░ąĮčŗ čéčĆąĄčģ čćąĖčüąĄą╗. |
